Toán 11 Kết nối tri thức bài 1

Giá trị lượng giác của góc lượng giác

Toán 11 Kết nối tri thức bài 1: Giá trị lượng giác của góc lượng giác

Bài 1.1 trang 16 SGK Toán 11 Kết nối tri thức
Bài 1.2 trang 16 SGK Toán 11 Kết nối tri thức
Bài 1.3 trang 16 SGK Toán 11 Kết nối tri thức
Bài 1.4 trang 16 SGK Toán 11 Kết nối tri thức
Bài 1.5 trang 16 SGK Toán 11 Kết nối tri thức
Bài 1.6 trang 16 SGK Toán 11 Kết nối tri thức

Giải Toán 11 Kết nối tri thức bài 1: Giá trị lượng giác của góc lượng giác được VnDoc.com tổng hợp và xin gửi tới bạn đọc cùng tham khảo để có thêm tài liệu giải bài tập Toán 11 Kết nối tri thức nhé. Mời bạn đọc cùng theo dõi.

Bài 1.1 trang 16 SGK Toán 11 Kết nối tri thức

Hoàn thành bảng sau

Số đo độ	$15 ^{\circ}$ $15 ^{\circ}$	?	$0^{\circ}$ $0^{\circ}$	$900^{\circ}$ $900^{\circ}$	?	?
Số đo radian	?	$\frac{3\pi }{8}$ $\frac{3\pi }{8}$	?	?	$-\frac{7\pi }{12}$ $-\frac{7\pi }{12}$	$-\frac{11\pi }{8}$ $-\frac{11\pi }{8}$

Lời giải chi tiết:

Số đo độ	$15 ^{\circ}$ $15 ^{\circ}$	$67.5^{\circ}$ $67.5^{\circ}$	$0^{\circ}$ $0^{\circ}$	$900^{\circ}$ $900^{\circ}$	$-105^{\circ}$ $-105^{\circ}$	$-247.5^{\circ}$ $-247.5^{\circ}$
Số đo radian	$\frac{\pi }{12}$ $\frac{\pi }{12}$	$\frac{3\pi }{8}$ $\frac{3\pi }{8}$	0	$5\pi$ $5\pi$	$-\frac{7\pi }{12}$ $-\frac{7\pi }{12}$	$-\frac{11\pi }{8}$ $-\frac{11\pi }{8}$

Bài 1.2 trang 16 SGK Toán 11 Kết nối tri thức

Một đường tròn có bán kính 20 cm. Tìm độ dài của các cung trên đường tròn đó có số đo sau:

a) $\frac{\pi }{12}$ $\frac{\pi }{12}$

b) 1.5

c) $35^{\circ}$ $35^{\circ}$

d) $315^{\circ}$ $315^{\circ}$

Lời giải chi tiết:

a) Độ dài cung đường tròn: $l=20\times \frac{\pi }{12}=5.236$ $l=20\times \frac{\pi }{12}=5.236$ (cm)

b) Độ dài cung đường tròn: $l=20\times 1.5=30$ $l=20\times 1.5=30$ (cm)

c) Đổi $35^{\circ}=\frac{7\pi }{36}$ $35^{\circ}=\frac{7\pi }{36}$

Độ dài cung đường tròn: $l=20\times \frac{7\pi }{36}=12.2173$ $l=20\times \frac{7\pi }{36}=12.2173$ (cm)

d) Đổi $315^{\circ}=\frac{7\pi }{4}$ $315^{\circ}=\frac{7\pi }{4}$

Độ dài cung đường tròn: $l=20\times \frac{7\pi }{4}=109.9557$ $l=20\times \frac{7\pi }{4}=109.9557$ (cm)

Bài 1.3 trang 16 SGK Toán 11 Kết nối tri thức

Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau:

a) $\frac{2\pi }{3}$ $\frac{2\pi }{3}$

b) $-\frac{11\pi }{4}$ $-\frac{11\pi }{4}$

c) $150^{\circ}$ $150^{\circ}$

d) $315^{\circ}$ $315^{\circ}$

Lời giải chi tiết

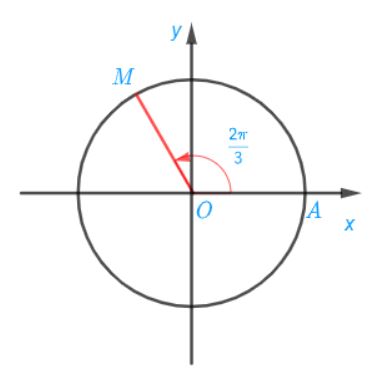
a) Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng $\frac{2\pi }{3}$ $\frac{2\pi }{3}$ được xác định trong hình sau:

Toán 11 Kết nối tri thức bài 1

b) Ta có: $-\frac{11\pi }{4}=-(\frac{3\pi }{4}+2\pi )$ $-\frac{11\pi }{4}=-(\frac{3\pi }{4}+2\pi )$

Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng $-\frac{11\pi }{4}$ $-\frac{11\pi }{4}$ được xác định trong hình sau:

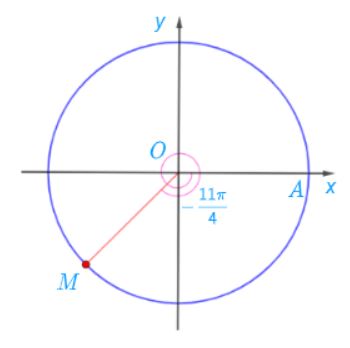
Toán 11 Kết nối tri thức bài 1

c) Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng 150° được xác định trong hình sau:

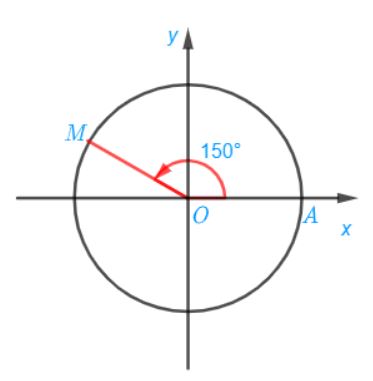
Toán 11 Kết nối tri thức bài 1

d) Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng – 225° được xác định trong hình sau:

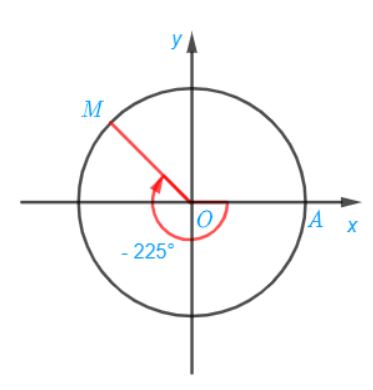
Toán 11 Kết nối tri thức bài 1

Bài 1.4 trang 16 SGK Toán 11 Kết nối tri thức

Tính các giá trị lượng giác góc $\alpha$ $\alpha$, biết

a) $cos\alpha =\frac{1}{5} và 0<\alpha <\frac{\pi }{2}$ $cos\alpha =\frac{1}{5} và 0<\alpha <\frac{\pi }{2}$

b) $sin\alpha =\frac{2}{3} và \frac{\pi }{2}<\alpha <\pi$ $sin\alpha =\frac{2}{3} và \frac{\pi }{2}<\alpha <\pi$

c) $tan\alpha =\sqrt{5} và \pi < \alpha <\frac{3\pi }{2}$ $tan\alpha =\sqrt{5} và \pi < \alpha <\frac{3\pi }{2}$

d) $cot\alpha =-\frac{1}{\sqrt{2}} và \frac{3\pi }{2}<\alpha <2\pi$ $cot\alpha =-\frac{1}{\sqrt{2}} và \frac{3\pi }{2}<\alpha <2\pi$

Lời giải chi tiết

a) Vì $0 < \alpha <\frac{\pi }{2}$ $0 < \alpha <\frac{\pi }{2}$ nên $sin \alpha > 0$ $sin \alpha > 0$

Mặt khác, từ $sin^{2}\alpha +cos^{2}\alpha =1$ $sin^{2}\alpha +cos^{2}\alpha =1$

suy ra $sin\alpha =\sqrt{1-cos^{2}\alpha }=\sqrt{1-\frac{1}{25}}=\frac{2\sqrt{6}}{5}$ $sin\alpha =\sqrt{1-cos^{2}\alpha }=\sqrt{1-\frac{1}{25}}=\frac{2\sqrt{6}}{5}$

Do đó, $tan\alpha =\frac{sin\alpha }{cos\alpha }=\frac{\frac{2\sqrt{6}}{5}}{\frac{1}{5}}=2\sqrt{6}$ $tan\alpha =\frac{sin\alpha }{cos\alpha }=\frac{\frac{2\sqrt{6}}{5}}{\frac{1}{5}}=2\sqrt{6}$ và $cot\alpha =\frac{1}{tan\alpha }=\frac{1}{2\sqrt{6}}$ $cot\alpha =\frac{1}{tan\alpha }=\frac{1}{2\sqrt{6}}$

b) Vì $\frac{\pi }{2}<\alpha <\pi$ $\frac{\pi }{2}<\alpha <\pi$ nên $cos\alpha<0$ $cos\alpha<0$

Mặt khác, từ $sin^{2}\alpha +cos^{2}\alpha =1$ $sin^{2}\alpha +cos^{2}\alpha =1$

Suy ra $cos\alpha =-\sqrt{1-sin^{2}\alpha }=-\sqrt{1-\frac{4}{9}}=-\frac{\sqrt{5}}{3}$ $cos\alpha =-\sqrt{1-sin^{2}\alpha }=-\sqrt{1-\frac{4}{9}}=-\frac{\sqrt{5}}{3}$

Do đó, $tan\alpha =\frac{sin\alpha }{cos\alpha }=\frac{\frac{2}{3}}{-\frac{\sqrt{5}}{3}}=-\frac{2\sqrt{5}}{5} và cot\alpha =\frac{1}{tan\alpha }=\frac{-\sqrt{5}}{2}$ $tan\alpha =\frac{sin\alpha }{cos\alpha }=\frac{\frac{2}{3}}{-\frac{\sqrt{5}}{3}}=-\frac{2\sqrt{5}}{5} và cot\alpha =\frac{1}{tan\alpha }=\frac{-\sqrt{5}}{2}$

c) $cot\alpha =\frac{1}{tan\alpha }=\frac{1}{2-\sqrt{5}}$ $cot\alpha =\frac{1}{tan\alpha }=\frac{1}{2-\sqrt{5}}$

Vì $\pi < \alpha <\frac{3\pi }{2}$ $\pi < \alpha <\frac{3\pi }{2}$ nên $cos\alpha <0,sin\alpha <0$ $cos\alpha <0,sin\alpha <0$

Mặt khác, từ $1+tan^{2}\alpha =\frac{1}{cos^{2}\alpha }$ $1+tan^{2}\alpha =\frac{1}{cos^{2}\alpha }$

suy ra $cos\alpha =-\sqrt{\frac{1}{1+tan^{2}\alpha }}=-\sqrt{\frac{1}{1+5}}=-\frac{1}{\sqrt{6}}$ $cos\alpha =-\sqrt{\frac{1}{1+tan^{2}\alpha }}=-\sqrt{\frac{1}{1+5}}=-\frac{1}{\sqrt{6}}$

Từ $1+cot^{2}\alpha =\frac{1}{sin^{2}\alpha }$ $1+cot^{2}\alpha =\frac{1}{sin^{2}\alpha }$

suy ra $sin\alpha =-\sqrt{\frac{1}{1+cot^{2}\alpha }}=-\sqrt{\frac{1}{1+\frac{1}{5}}}=-\frac{\sqrt{30}}{6}$ $sin\alpha =-\sqrt{\frac{1}{1+cot^{2}\alpha }}=-\sqrt{\frac{1}{1+\frac{1}{5}}}=-\frac{\sqrt{30}}{6}$

d) $tan\alpha =\frac{1}{cot\alpha }=-\sqrt{2}$ $tan\alpha =\frac{1}{cot\alpha }=-\sqrt{2}$

Vì $\frac{3\pi }{2}<\alpha <2\pi$ $\frac{3\pi }{2}<\alpha <2\pi$ nên $cos\alpha >0,sin\alpha <0$ $cos\alpha >0,sin\alpha <0$

Mặt khác, từ $1+tan^{2}\alpha =\frac{1}{cos^{2}\alpha }$ $1+tan^{2}\alpha =\frac{1}{cos^{2}\alpha }$

suy ra $cos\alpha =\sqrt{\frac{1}{1+tan^{2}\alpha }}=\sqrt{\frac{1}{1+2}}=\frac{1}{\sqrt{3}}$ $cos\alpha =\sqrt{\frac{1}{1+tan^{2}\alpha }}=\sqrt{\frac{1}{1+2}}=\frac{1}{\sqrt{3}}$

Từ $1+cot^{2}\alpha =\frac{1}{sin^{2}\alpha }$ $1+cot^{2}\alpha =\frac{1}{sin^{2}\alpha }$

suy ra $sin\alpha =-\sqrt{\frac{1}{1+cot^{2}\alpha }}=-\sqrt{\frac{1}{1+\frac{1}{2}}}=-\frac{\sqrt{6}}{3}$ $sin\alpha =-\sqrt{\frac{1}{1+cot^{2}\alpha }}=-\sqrt{\frac{1}{1+\frac{1}{2}}}=-\frac{\sqrt{6}}{3}$

Bài 1.5 trang 16 SGK Toán 11 Kết nối tri thức

Chứng minh các đẳng thức:

a) $cos^{4}\alpha -sin^{4}\alpha =2cos^{2}\alpha -1$ $cos^{4}\alpha -sin^{4}\alpha =2cos^{2}\alpha -1$

b) $\frac{cos^{2}\alpha +tan^{2}\alpha -1}{sin^{2}\alpha }=tan^{2}\alpha$ $\frac{cos^{2}\alpha +tan^{2}\alpha -1}{sin^{2}\alpha }=tan^{2}\alpha$

Lời giải chi tiết

a) $cos^{4}\alpha -sin^{4}\alpha =(cos^{2}\alpha +sin^{2}\alpha )(cos^{2}\alpha -sin^{2}\alpha )$ $cos^{4}\alpha -sin^{4}\alpha =(cos^{2}\alpha +sin^{2}\alpha )(cos^{2}\alpha -sin^{2}\alpha )$

$=1\times (cos^{2}\alpha -sin^{2}\alpha )=cos^{2}\alpha -(1-sin^{2}\alpha )=2cos^{2}\alpha -1$ $=1\times (cos^{2}\alpha -sin^{2}\alpha )=cos^{2}\alpha -(1-sin^{2}\alpha )=2cos^{2}\alpha -1$

b) $\frac{cos^{2}\alpha +tan^{2}\alpha -1}{sin^{2}\alpha }=\frac{cos^{2}\alpha }{sin^{2}\alpha }+\frac{tan^{2}\alpha }{sin^{2}\alpha }-\frac{1}{sin^{2}\alpha }$ $\frac{cos^{2}\alpha +tan^{2}\alpha -1}{sin^{2}\alpha }=\frac{cos^{2}\alpha }{sin^{2}\alpha }+\frac{tan^{2}\alpha }{sin^{2}\alpha }-\frac{1}{sin^{2}\alpha }$

$=cot^{2}\alpha +\frac{\frac{sin^{2}\alpha }{cos^{2}\alpha }}{sin^{2}\alpha }-(1+cot^{2}\alpha )=\frac{1}{cos^{2}}-1=tan^{2}\alpha$ $=cot^{2}\alpha +\frac{\frac{sin^{2}\alpha }{cos^{2}\alpha }}{sin^{2}\alpha }-(1+cot^{2}\alpha )=\frac{1}{cos^{2}}-1=tan^{2}\alpha$

Bài 1.6 trang 16 SGK Toán 11 Kết nối tri thức

Bánh xe của người đi xe đạp quay được 11 vòng trong 5 giây

a) Tính góc (theo độ và radian) mà bánh xe quay được trong 1 giây

b) Tính độ dài quãng đường mà người đi xe đã đi được trong 1 phút, biết rằng đường kính của bánh xe đạp là 680mm

Lời giải chi tiết

a) 1 giây bánh xe quay được số vòng là: $11:5=\frac{11}{5}$ $11:5=\frac{11}{5}$ (vòng)

Góc mà bánh xe quay được trong 1 giây: $\frac{11}{5}\times 360^{\circ}=792^{\circ}=4.4\pi$ $\frac{11}{5}\times 360^{\circ}=792^{\circ}=4.4\pi$ (rad)

b) Ta có: 1 phút = 60 giây.

Trong 1 phút bánh xe quay được $60\times \frac{11}{5}=132$ $60\times \frac{11}{5}=132$ vòng.

Chu vi của bánh xe đạp là: C = 680π (mm).

Quãng đường mà người đi xe đạp đã đi được trong một phút là

680π\times 132 = 89 760π (mm) = 89,76π (m).

Trắc nghiệm Giá trị lượng giác của góc lượng giác

Bài trắc nghiệm số: 4186

Toán 11 Kết nối tri thức bài 2

Chia sẻ, đánh giá bài viết

3

1.966

Bài trước

Bài sau

Chia sẻ bởi:
Nguyễn Linh An
Ngày: 05/09/2024

Sắp xếp theo

Xóa Đăng nhập để Gửi

Toán 11

Gợi ý cho bạn

Xem thêm