Toán 11 Kết nối tri thức bài 31
Toán 11 Kết nối tri thức bài 31: Định nghĩa và ý nghĩa của đạo hàm
VnDoc.com xin gửi tới bạn đọc bài viết Toán 11 Kết nối tri thức bài 31: Định nghĩa và ý nghĩa của đạo hàm để bạn đọc cùng tham khảo. Mong rằng qua bài viết này bạn đọc có thêm tài liệu để giải bài tập Toán 11 Kết nối tri thức. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây.
Bài 9.1 trang 86 SGK Toán 11 Kết nối
Tính (bằng định nghĩa) đạo hàm của các hàm số sau:
a) y = x2 – x tại x0 = 1;
b) y = −x3 tại x0 = −1.
Bài làm
a) 
\(f'(1) = \lim_{h \to 0} \frac{f(1+h) - f(1)}{h}\)
\(= \lim_{h \to 0} \frac{(1+h)^{2} - (1+h) - (1^{2} - 1)}{h}\)
\(= \lim_{h \to 0} \frac{1 + 2h + h^{2} - 1 - h - 1 + 1}{h}\)
\(= \lim_{h \to 0} \frac{h^{2} + h}{h}\)
\(= \lim_{h \to 0} (h + 1)\)
= 1 + 1
= 2
b) \(f'(-1) = \lim_{h \to 0} \frac{f(-1+h) - f(-1)}{h}\)
\(= \lim_{h \to 0} \frac{-(h-1)^{3} + 1^{3}}{h}\)
\(= \lim_{h \to 0} \frac{-h^{3} + 3h^{2} - 3h}{h}\)
\(= \lim_{h \to 0} (-h^{2} + 3h - 3)\)
= 3
Bài 9.2 trang 86 SGK Toán 11 Kết nối
Sử dụng định nghĩa, tìm đạo hàm của các hàm số sau:
a)y = kx2 + c (với k, c là các hằng số);
b) y = x3
Bài làm
a) \(f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}\)
\(= \lim_{h \to 0} \frac{k(x+h)^{2}+c - (kx^{2}+c)}{h}\)
\(= \lim_{h \to 0} \frac{kx^{2}+2kxh+kh^{2}+c-kx^{2}-c}{h}\)
\(= \lim_{h \to 0} \frac{2kxh+kh^{2}}{h}\)
\(= \lim_{h \to 0} (2kx + kh)\)
= 2kx
b) \(f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}\)
\(= \lim_{h \to 0} \frac{(x+h)^{3}-x^{3}}{h}\)
\(= \lim_{h \to 0} \frac{x^{3}+3x^{2}h+3xh^{2}+h^{3}-x^{3}}{h}\)
\(= \lim_{h \to 0} \frac{3x^{2}h+3xh^{2}+h^{3}}{h}\)
\(= \lim_{h \to 0} (3x^{2}+3xh+h^{2})\)
\(= 3x^{2}\)
Bài 9.3 trang 86 SGK Toán 11 Kết nối
Viết phương trình tiếp tuyến của parabol y = −x2 + 4x, biết:
a) Tiếp điểm có hoành độ x0 = 1;
b) Tiếp điểm có tung độ y0 = 0.
Bài làm
a) Đạo hàm của hàm số tại điểm \(x_{0}\)
\(f^{'}(x)=-2x+4\)
đạo hàm của hàm số tại điểm \(x_{0}=1\)
\(f ^{'}(1)=-2(1)+4=2\)
phương trình tiếp tuyến của parabol tại điểm \(x_{0}=1\) là:
\(y-f(x_{0})=f^{'}(x_{0})(x-(x_{0})\Rightarrow y-f(1)=2(x-1)\)
Thay f(1) = 3 , ta được phương trình tiếp tuyến:
\(y-3 =2(x-1)\Rightarrow y=2x+1\)
b) Tại điểm \(y_0=0\) ta có x = 2
Đường tiếp tuyến tại điểm (2,0) có độ dốc bằng\(y'=-2\times2+4=-4\). Sử dụng công thức tương tự, ta có:
\(y-0 =- 4(x-2)\Rightarrow y= -4x+8\)
Bài 9.4 trang 86 SGK Toán 11 Kết nối
Một vật được phóng theo phương thẳng đứng lên trên từ mặt đất với vận tốc ban đầu là 19,6 m/s thì độ cao h của nó (tính bằng mét) sau t giây được cho bởi công thức h = 19,6t – 4,9t2. Tìm vận tốc của vật khi nó chạm đất.
Bài 9.5 trang 86 SGK Toán 11 Kết nối
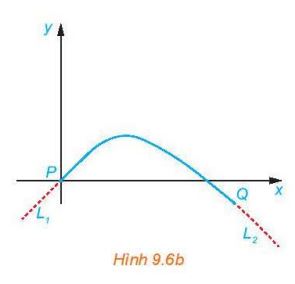
Một kĩ sư thiết kế một đường ray tàu lượn, mà mặt cắt của nó gồm một cung đường cong có dạng parabol (H.9.6a), đoạn dốc lên L1, và đoạn dốc xuống L2, là những phần đường thẳng có hệ số góc lần lượt là 0,5 và –0,75. Để tàu lượn chạy êm và không bị đổi hướng đột ngột, L1 và L2 phải là những tiếp tuyến của cung parabol tại các điểm chuyển tiếp P và Q (H.9.6b). Giả sử gốc toạ độ đặt tại P và phương trình của parabol là y = ax2 + bx + c, trong đó x tính bằng mét.
a) Tìm c.
b) Tính y'(0) và tìm b.
c) Giả sử khoảng cách theo phương ngang giữa P và Q là 40 m. Tìm a.
d) Tìm chênh lệch độ cao giữa hai điểm chuyển tiếp P và Q.
-------------------------------
Bài tiếp theo: Toán 11 Kết nối tri thức bài 32
VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Kết nối tri thức bài 31: Định nghĩa và ý nghĩa của đạo hàm. Hi vọng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 11 Kết nối tri thức. Mời các bạn cùng tham khảo thêm tại mục Ngữ văn 11 Kết nối tri thức.
