Toán 11 Kết nối tri thức bài 15

Giới hạn của dãy số

Toán 11 Kết nối tri thức bài 15: Giới hạn của dãy số

Bài 5.1 trang 109 SGK Toán 11 Kết nối tri thức
Bài 5.2 trang 109 SGK Toán 11 Kết nối tri thức
Bài 5.3 trang 109 SGK Toán 11 Kết nối tri thức
Bài 5.4 trang 109 SGK Toán 11 Kết nối tri thức
Bài 5.5 trang 109 SGK Toán 11 Kết nối tri thức
Bài 5.6 trang 109 SGK Toán 11 Kết nối tri thức

Toán 11 Kết nối tri thức bài 15: Giới hạn của dãy số được VnDoc.com tổng hợp và xin gửi tới bạn đọc cùng tham khảo. Hi vọng qua đây bạn đọc có thể dễ dàng giải bài tập Toán 11 Kết nối tri thức nhé. Mời các bạn cùng theo dõi bài viết.

Bài 5.1 trang 109 SGK Toán 11 Kết nối tri thức

Tìm các giới hạn sau:

a) $\underset{n\rightarrow +\infty }{lim}\frac{n^{2}+n+1}{2n^{2}+1}$ $\underset{n\rightarrow +\infty }{lim}\frac{n^{2}+n+1}{2n^{2}+1}$

b) $\underset{n\rightarrow +\infty }{lim}(\sqrt{n^{2}+2n}-n)$ $\underset{n\rightarrow +\infty }{lim}(\sqrt{n^{2}+2n}-n)$

Lời giải

a) $\underset{n\rightarrow +\infty }{lim}\frac{n^{2}+n+1}{2n^{2}+1}=\underset{n\rightarrow +\infty }{lim}\frac{1+\frac{1}{n}+\frac{1}{n^{2}}}{2+\frac{1}{n^{2}}}=\frac{\underset{n\rightarrow +\infty }{lim}(1+\frac{1}{n}+\frac{1}{n^{2}})}{\underset{n\rightarrow +\infty }{lim}(2+\frac{1}{n^{2}})}=\frac{1}{2}$ $\underset{n\rightarrow +\infty }{lim}\frac{n^{2}+n+1}{2n^{2}+1}=\underset{n\rightarrow +\infty }{lim}\frac{1+\frac{1}{n}+\frac{1}{n^{2}}}{2+\frac{1}{n^{2}}}=\frac{\underset{n\rightarrow +\infty }{lim}(1+\frac{1}{n}+\frac{1}{n^{2}})}{\underset{n\rightarrow +\infty }{lim}(2+\frac{1}{n^{2}})}=\frac{1}{2}$

b)

$\underset{n\rightarrow +\infty }{lim}v_{n}=\underset{n\rightarrow +\infty }{lim}(\sqrt{2n^{2}+1}-n)=\underset{n\rightarrow +\infty }{lim}\frac{n^{2}+2n-n^{2}}{\sqrt{n^{2}+2n}+n}=\underset{n\rightarrow +\infty }{lim}\frac{2n}{n(\sqrt{1+\frac{2}{n}}+1)}=\underset{n\rightarrow +\infty }{lim}\frac{2}{\sqrt{1+\frac{2}{n}}+1}=1$ $\underset{n\rightarrow +\infty }{lim}v_{n}=\underset{n\rightarrow +\infty }{lim}(\sqrt{2n^{2}+1}-n)=\underset{n\rightarrow +\infty }{lim}\frac{n^{2}+2n-n^{2}}{\sqrt{n^{2}+2n}+n}=\underset{n\rightarrow +\infty }{lim}\frac{2n}{n(\sqrt{1+\frac{2}{n}}+1)}=\underset{n\rightarrow +\infty }{lim}\frac{2}{\sqrt{1+\frac{2}{n}}+1}=1$

Bài 5.2 trang 109 SGK Toán 11 Kết nối tri thức

Cho hai dãy số không âm $(u_{n}) và (v_{n})$ $(u_{n}) và (v_{n})$ với $\underset{n\rightarrow +\infty }{lim}u_{n}=2$ $\underset{n\rightarrow +\infty }{lim}u_{n}=2$ và $\underset{n\rightarrow +\infty }{lim}v_{n}=3$ $\underset{n\rightarrow +\infty }{lim}v_{n}=3$

Tìm các giới hạn sau:

a) $\underset{n\rightarrow +\infty }{lim}\frac{u_{n}^{2}}{v_{n}-u_{n}}$ $\underset{n\rightarrow +\infty }{lim}\frac{u_{n}^{2}}{v_{n}-u_{n}}$

b) $\underset{n\rightarrow +\infty }{lim}\sqrt{u_{n}+2v_{n}}$ $\underset{n\rightarrow +\infty }{lim}\sqrt{u_{n}+2v_{n}}$

Lời giải

a) $\underset{n\rightarrow +\infty }{lim}\frac{u_{n}^{2}}{v_{n}-u_{n}}=\frac{(\underset{n\rightarrow +\infty }{lim}u_{n})^{2}}{\underset{n\rightarrow +\infty }{lim}v_{n}-\underset{n\rightarrow +\infty }{lim}u_{n}}=\frac{2^{2}}{3-2}=4$ $\underset{n\rightarrow +\infty }{lim}\frac{u_{n}^{2}}{v_{n}-u_{n}}=\frac{(\underset{n\rightarrow +\infty }{lim}u_{n})^{2}}{\underset{n\rightarrow +\infty }{lim}v_{n}-\underset{n\rightarrow +\infty }{lim}u_{n}}=\frac{2^{2}}{3-2}=4$

b) $\underset{n\rightarrow +\infty }{lim}(u_{n}+2v_{n})=\underset{n\rightarrow +\infty }{lim}u_{n}+2\underset{n\rightarrow +\infty }{lim}v_{n}=2+2\times 3=8\Rightarrow \underset{n\rightarrow +\infty }{lim}\sqrt{u_{n}+2v_{n}}=\sqrt{8}$ $\underset{n\rightarrow +\infty }{lim}(u_{n}+2v_{n})=\underset{n\rightarrow +\infty }{lim}u_{n}+2\underset{n\rightarrow +\infty }{lim}v_{n}=2+2\times 3=8\Rightarrow \underset{n\rightarrow +\infty }{lim}\sqrt{u_{n}+2v_{n}}=\sqrt{8}$

Bài 5.3 trang 109 SGK Toán 11 Kết nối tri thức

Tìm giới hạn của các dãy số cho bởi:

a) $u_{n}=\frac{n^{2}+1}{2n-1}$ $u_{n}=\frac{n^{2}+1}{2n-1}$

b) $v_{n}=\sqrt{2n^{2}+1}-n$ $v_{n}=\sqrt{2n^{2}+1}-n$

Lời giải

a) $\underset{n\rightarrow +\infty }{lim}u_{n}=\underset{n\rightarrow +\infty }{lim}\frac{n^{2}+1}{2n-1}=\underset{n\rightarrow +\infty }{lim}\frac{1+\frac{1}{n^{2}}}{\frac{2}{n}-\frac{1}{n^{2}}}=\frac{\underset{n\rightarrow +\infty }{lim}(1+\frac{1}{n^{2}})}{\underset{n\rightarrow +\infty }{lim}(\frac{2}{n}-\frac{1}{n^{2}})}$ $\underset{n\rightarrow +\infty }{lim}u_{n}=\underset{n\rightarrow +\infty }{lim}\frac{n^{2}+1}{2n-1}=\underset{n\rightarrow +\infty }{lim}\frac{1+\frac{1}{n^{2}}}{\frac{2}{n}-\frac{1}{n^{2}}}=\frac{\underset{n\rightarrow +\infty }{lim}(1+\frac{1}{n^{2}})}{\underset{n\rightarrow +\infty }{lim}(\frac{2}{n}-\frac{1}{n^{2}})}$

Ta có: $\underset{n\rightarrow +\infty }{lim}(1+\frac{1}{n^{2}})=1,\underset{n\rightarrow +\infty }{lim}(\frac{2}{n}-\frac{1}{n^{2}})=0 suy ra \underset{n\rightarrow +\infty }{lim}u_{n}=+\infty$ $\underset{n\rightarrow +\infty }{lim}(1+\frac{1}{n^{2}})=1,\underset{n\rightarrow +\infty }{lim}(\frac{2}{n}-\frac{1}{n^{2}})=0 suy ra \underset{n\rightarrow +\infty }{lim}u_{n}=+\infty$

b) $\underset{n\rightarrow +\infty }{lim}v_{n}=\underset{n\rightarrow +\infty }{lim}\sqrt{2n^{2}+1}-n=\underset{n\rightarrow +\infty }{lim}\frac{2n^{2}+1-n^{2}}{\sqrt{2n^{2}+1}+n}$ $\underset{n\rightarrow +\infty }{lim}v_{n}=\underset{n\rightarrow +\infty }{lim}\sqrt{2n^{2}+1}-n=\underset{n\rightarrow +\infty }{lim}\frac{2n^{2}+1-n^{2}}{\sqrt{2n^{2}+1}+n}$

$=\underset{n\rightarrow +\infty }{lim}\frac{n^{2}+1}{n^{2}(\sqrt{\frac{2}{n^{2}}+\frac{1}{n^{4}}}+\frac{1}{n})}=\underset{n\rightarrow +\infty }{lim}\frac{1+\frac{1}{n^{2}}}{\sqrt{\frac{2}{n^{2}}+\frac{1}{n^{4}}}+\frac{1}{n}}=+\infty$ $=\underset{n\rightarrow +\infty }{lim}\frac{n^{2}+1}{n^{2}(\sqrt{\frac{2}{n^{2}}+\frac{1}{n^{4}}}+\frac{1}{n})}=\underset{n\rightarrow +\infty }{lim}\frac{1+\frac{1}{n^{2}}}{\sqrt{\frac{2}{n^{2}}+\frac{1}{n^{4}}}+\frac{1}{n}}=+\infty$

Bài 5.4 trang 109 SGK Toán 11 Kết nối tri thức

Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số:

a) 1,(12) = 1,121212...

b) 3,(102) = 3,102102102...

Lời giải

a) 1,121212...= 1 + 0,12 + 0,0012 + 0,000012 + ...

= $1 +12\times 10^{-2}+12\times 10^{-4}+12\times 10^{-6}+$ $1 +12\times 10^{-2}+12\times 10^{-4}+12\times 10^{-6}+$...

$12\times 10^{-2}+12\times 10^{-4}+12\times 10^{-6}+$ $12\times 10^{-2}+12\times 10^{-4}+12\times 10^{-6}+$... là tổng cấp số nhân lùi vô hạn với $u_{1}=12\times 10^{-2},q=10^{-2} nên 1,121212...=1+\frac{u_{1}}{1-q}=1+\frac{12\times 10^{-2}}{1-10^{-2}}=\frac{37}{33}$ $u_{1}=12\times 10^{-2},q=10^{-2} nên 1,121212...=1+\frac{u_{1}}{1-q}=1+\frac{12\times 10^{-2}}{1-10^{-2}}=\frac{37}{33}$

b) 3,102102102... = 3 + 0,102 + 0,000102 + 0,000000102 +...

= $3+102\times 10^{-3}+102\times 10^{-6}+102\times 10^{-9}$ $3+102\times 10^{-3}+102\times 10^{-6}+102\times 10^{-9}$...

$102\times 10^{-3}+102\times 10^{-6}+102\times 10^{-9}+$ $102\times 10^{-3}+102\times 10^{-6}+102\times 10^{-9}+$... là tổng cấp số nhân lùi vô hạn với $u_{1}=102\times 10^{-3}, q=10^{-3} nên 3,(102)=3+\frac{u_{1}}{1-q}=3+\frac{102\times 10^{-3}}{1-10^{-3}}=\frac{1033}{333}$ $u_{1}=102\times 10^{-3}, q=10^{-3} nên 3,(102)=3+\frac{u_{1}}{1-q}=3+\frac{102\times 10^{-3}}{1-10^{-3}}=\frac{1033}{333}$

Bài 5.5 trang 109 SGK Toán 11 Kết nối tri thức

Một bệnh nhân hàng ngày phải uống một viên thuốc 150mg. Sau ngày đầu, trước mỗi lần uống, hàm lượng thuốc cũ trong cơ thể vẫn còn 5%. Tính lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ 5. Ước tính lượng thuốc trong cơ thể nếu bệnh nhân sử dụng thuốc trong một thời gian dài.

Lời giải

Đang cập nhật...

Bài 5.6 trang 109 SGK Toán 11 Kết nối tri thức

Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng α (H.5.3). Từ A kẻ AA₁ ⊥ BC, từ A₁ kẻ A₁A₂ ⊥ AC, sau đó lại kẻ A₂A₃ ⊥ BC. Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn $AA_{1}A_{2}A_{3}$ $AA_{1}A_{2}A_{3}$... Tính độ dài đường gấp khúc này theo h và α

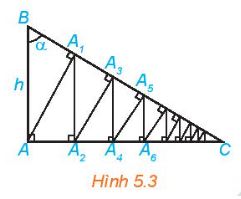
Toán 11 Kết nối tri thức bài 15

Lời giải

Độ dài đường gấp khúc tạo thành cấp số nhân với số hạng tổng quát là: u_n = sinα × h × (sinα)ⁿ⁻¹

Độ dài đường gấp khúc: AA₁ + A₂A₃ +....

Đây là tổng của cấp số nhân lùi vô hạn với u₁ = sinα × h, q = sinα nên AA₁ + A₂A₃ + .... = $\frac{sinα × h}{1 − sinα}$ $\frac{sinα × h}{1 − sinα}$

-------------------------

Toán 11 Kết nối tri thức bài 16

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Kết nối tri thức bài 15: Giới hạn của dãy số. Mong rằng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 11 Kết nối tri thức. Mời các bạn cùng tham khảo thêm tại mục Ngữ văn 11 Kết nối tri thức.

Chia sẻ, đánh giá bài viết

1

350

Bài trước

Bài sau