Toán 11 Kết nối tri thức bài 26
Toán 11 Kết nối tri thức bài 26: Khoảng cách
VnDoc.com xin gửi tới bạn đọc bài viết Toán 11 Kết nối tri thức bài 26: Khoảng cách để bạn đọc cùng tham khảo. Hi vọng qua bài viết này bạn đọc có thể dễ dàng giải bài tập Toán 11 Kết nối tri thức. Mời các bạn cùng theo dõi bài viết dưới đây.
Bài 7.22 trang 59 SGK Toán 11 Kết nối
Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a, mặt bên SAD là một tam giác đều và (SAD) ⊥ (ABCD).
a) Tính chiều cao của hình chóp.
b) Tính khoảng cách giữa BC và (SAD).
c) Xác định đường vuông góc chung và tính khoảng cách giữa AB và SD.
Bài làm
Gọi H là trung điểm AB . Khi đó, SH là đường cao của tam giác đều SAD. Vì ABCD là hình vuông nên AH song song với mặt phẳng (SAD). Suy ra SH vuông góc với mặt phẳng đáy ABCD. Ta có:
\(SH=\frac{\sqrt{3}}{2}a\)
Gọi O là trung diểm của SD. Khi đó OB // (SAD) và OB = \(\frac{\sqrt{2}}{2}a\). Ta có khoảng cách từ C dến (SAD). Để làm được điều này, ta cần tìm giao tuyến của hai mặt phẳng (SAD) và (BCD). Gọi E là iao điểm của BD và SH. Khi đó SE song song với BC và \(BE= \frac{1}{\sqrt{2}}a\)
\(CE=BE-BC=\frac{1}{\sqrt{2}}a-a=(\frac{1}{\sqrt{2}}-1)a\)
Ta lại có OE vuông góc với (SAD) và \(OE= \frac{1}{2} SH= \frac{\sqrt{3}}{4}a\) Khoảng cách từ C đến (SAD) là khoảng cách từ C đến OE hay
\(d_{BC,(SAD)}=\frac{CE}{sin\widehat{CEO}}=\frac{\sqrt{2}}{4-2\sqrt{2}}a=(2+\sqrt{2})a\)
c) Đường vuông góc chung của hai mặt phẳng (SAB) và (SCD) là đường thẳng \(\delta\) đi qua trung điẻm của AC và BD. Suy ra \(\delta\) và AB
Gọi M là trung điểm cua AC và N là trung điểm ủa BD. Khi đó, SM vuông góc với (SAB) và SN vuông góc với (SCD). Suy ra \(\delta\) vuông góc với cả hai mặt phẳng
\(MN=\frac{1}{2}AC=\frac{\sqrt{2}}{2}a\)
Khoảng cách giữa \(\delta\) và AB bằng khoảng cách từ điểm S đến đường thẳng AB theo công thức khoảng cách từ một điểm đến một đường:
\(d_{S,AC}=\frac{\left | SA.AB.SB \right |}{2S_{SAB}}=\frac{\sqrt6}{3}a\)
Bài 7.23 trang 59 SGK Toán 11 Kết nối
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = b, BC = c.
a) Tính khoảng cách giữa CC' và (BB'D'D).
b) Xác định đường vuông góc chung và tính khoảng cách giữa AC và B'D'.
Bài làm
Gọi O là trung điểm của BB′. Ta cần tính khoảng cách từ C đến (BB′D′D), hay khoảng cách từ C đến OO′. Khoảng cách này bằng khoảng cách từ C đến mặt phẳng (BO′O) nhân với cos \(\widehat{CO'O}\)
\(cos \widehat{CO'O}=\frac{CO'}{CC'}=\frac{\frac{1}{2}c}{\sqrt{a^{2}+(\frac{1}{2}b)^{2}+(\frac{1}{2}c)^{2}}}\)
Để xác định khoảng cách từ C đến (BB′D′D), ta cần biết d(O′,(BO′O)). Khi đó, khoảng cách cần tìm chính là:
\(d_{CC',BB'D'D}=d(C,(BO'O))cos \widehat{CO'O}\)
\(=\frac{c}{\sqrt{a^{2}+(\frac{1}{2}b)^{2}+(\frac{1}{2}c)^{2}}}.\frac{\frac{1}{2}c}{\sqrt{a^{2}+(\frac{1}{2}b)^{2}+(\frac{1}{2}c)^{2}}}\)
b) Đường vuông góc chung của hai mặt phẳng (ABC) và (B'C'D') la đường thẳng \(\delta\) di qua trung điểm của BD và song song với ABCD .
Gọi M là trung điểm của BD,N là trung điểm của B'D',P là trung điểm của AD,Q là trung điểm A'C' . Khi đó \(\delta\) là đường thẳng vuông góc với mặt phẳng (ABCD) qua M , suy ra \(\delta\) vuông góc với AC
\(MN=\frac{1}{2}BD=\frac{\sqrt{a^{2}+b^{2}+c^{2}}}{2},PQ=\frac{\sqrt{a^{2}+b^{2}+c^{2}}}{2}\)
\(d_{\Delta ,AC}=\frac{\left | AM.AC.CM \right |}{2S_{ABC}}=\frac{\sqrt{(a^{2}+c^{2})(b^{2}+c^{2})}}{2c}\)
Bài 7.24 trang 59 SGK Toán 11 Kết nối
Cho tứ diện ABCD có các cạnh đều bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh rằng:
a) MN là đường vuông góc chung của AB và CD.
b) Các cặp cạnh đối diện trong tứ diện ABCD đều vuông góc với nhau.
Bài làm
a) Gọi O là trung điểm của AC, ta có OM = 1/2 AB = 1/2CD (do ABCD là hình cầu). Vì vậy, OMCD là hình bình hành.
Suy ra, OM // CD. Tương tự, ta chứng minh được ON // AB. Do đó, MN là đường chéo của hình bình hành OMCD, nên MN vuông góc với CD và AB.
b)Gọi O là tâm của hình cầu, ta có OA = OB = OC = OD, do các cạnh đều bằng nhau. Từ đó, ta suy ra các tam giác OAB, OBC, OCD, ODA đều đồng dạng.
Mặt khác, ta biết OM = ON, do M, N lần lượt là trung điểm của AB, CD. Suy ra, tam giác OMN cũng đồng dạng với OAB, OBC, OCD, ODA.
Do đó, các góc tạo bởi các cặp cạnh đối diện trong tứ diện đều bằng nhau, mỗi góc bằng π/2 (do OAB, OBC, OCD, ODA là tam giác vuông), nên chúng đều vuông góc với nhau.
Bài 7.25 trang 59 SGK Toán 11 Kết nối
Cho hình lập phương ABCD.A'B'C'D' có cạnh a.
a) Chứng minh rằng hai mặt phẳng (D'AC) và (BC'A') song song với nhau và DB' vuông góc với hai mặt phẳng đó.
b) Xác định các giao điểm E, F của DB' với (D'AC), (BC'A'). Tính d(D'AC), (BC'A')).
Bài làm
a) Gọi O là tâm của hình lập phương, M là trung điểm của AB và N là trung điểm của A′C′. Ta có OM // D′A′C′ và ON // BC′A′ do OM và ON là đường trung bình của các cạnh tương ứng.
Do đó, (D′AC) // (BC′A′). Từ đó, ta có DB′ ⊥ (D′AC) và DB′ ⊥ (BC′A′), vì DB′ song song với cạnh AA′ và vuông góc với mặt phẳng chứa AA′.
Bài 7.26 trang 59 SGK Toán 11 Kết nối
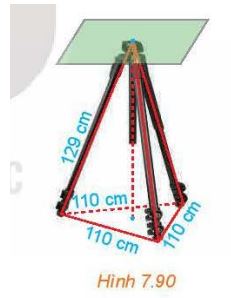
Giá đỡ ba chân ở Hình 7.90 đang được mở sao cho ba gốc chân cách đều nhau một khoảng cách bằng 110 cm. Tính chiều cao của giá đỡ, biết các chân của giá đỡ dài 129 cm.
Bài 7.27 trang 59 SGK Toán 11 Kết nối
Một bể nước có đáy thuộc mặt phẳng nằm ngang. Trong trường hợp này, độ sâu của bể là khoảng cách giữa mặt nước và đáy bể. Giải thích vì sao để đo độ sâu của bể, ta có thể thả quả dọi chạm đáy bể và đo chiều dài của đoạn dây dọi năm trong bề nước.
--------------------------------------
Bài tiếp theo: Toán 11 Kết nối tri thức bài 27
Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Kết nối tri thức bài 26: Khoảng cách. Mong rằng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 11 Kết nối tri thức. Mời các bạn cùng tham khảo thêm tại mục Ngữ văn 11 Kết nối tri thức.
