Toán 11 Kết nối tri thức bài 11

VnDoc.com xin gửi tới bạn đọc bài viết Toán 11 Kết nối tri thức bài 11: Hai đường thẳng song song để bạn đọc cùng tham khảo. Hi vọng qua đây bạn đọc có thể dễ dàng giải bài tập Toán 11 Kết nối tri thức nhé. Mời các bạn cùng theo dõi.

Bài 4.9 trang 82 SGK Toán 11 Kết nối tri thức

Trong không gian, cho ba đường thẳng a, b, c. Những mệnh đè nào sau đây đúng?

a) Nếu a và b không cắt nhau thì a và b song song

b) Nếu b và c chéo nhau thì b và c không cùng thuộc một mặt phẳng

c) Nếu a và b cùng song song với c thì a song song với b

d) Nếu a và b cắt nhau, b và c cắt nhau thì a và c cắt nhau

Lời giải

a) Sai. Vì nếu a và b không cắt nhua thì a và b có thể song song hoặc chéo nhau.

b) Đúng.

c) Đúng

d) Sai. VÌ a và c cũng có thể chéo nhau.

Bài 4.10 trang 82 SGK Toán 11 Kết nối tri thức

Cho hình chóp S.ABCD có đáy là hình bình hành. Trong các cặp đường thẳng sau, cặp đường thẳng nào cắt nhau, cặp đường thẳng nào song song, cặp đường thẳng nào chéo nhau?

a) AB và CD

b) AC và BD

c) SB và CD

Lời giải

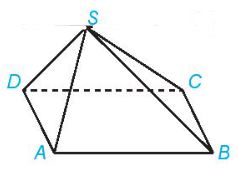
a) AB và CD song song với nhau

b) AC và BD cắt nhau

c) SB và CD chéo nhau

Bài 4.11 trang 82 SGK Toán 11 Kết nối tri thức

Cho hình chóp S.ABCD có đáy ABCD là ình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh bên SA, SB, SC, SD (H.4.27). Chứng minh rằng tứ giác MNPQ là hình bình hành.

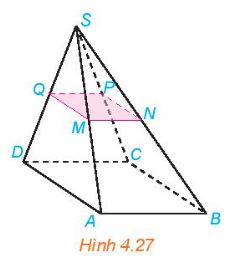
Lời giải

Xét tam giác SAB ta có: MN là đường trung bình suy ra MN // AB

Tương tự ta có: NP // BC, PQ // CD, MQ // AD

Mà ABCD là hình bình hành nên AB // CD, AD// CD, suy ra MN // PQ, MQ // NP

Như vậy, MNPQ là hình bình hành

Bài 4.12 trang 82 SGK Toán 11 Kết nối tri thức

Cho hình chóp S. ABCD có đáy ABCD là hình thang (AB // CD). Gọi M, N lần lượt là trung điểm của các cạnh SA, SB. Chứng minh rằng tứ giác MNCD là hình thang

Lời giải

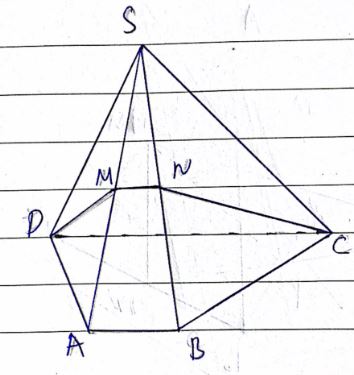
Xét tam giác SAB ta có MN là đường trung bình suy ra MN // AB

Mà AB // CD do đó MN // CD

Suy ra MNCD là hình thang

Bài 4.13 trang 82 SGK Toán 11 Kết nối tri thức

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M là trung điểm của đoạn thẳng SD (H.4.28)

a) Xác định giao tuyến của mặt phẳng (MAB) và (SCD)

b) Gọi N là giao điểm của đường thẳng SC và mặt phẳng (MAB). Chứng minh rằng MN là đường trung bình của tam giác SCD

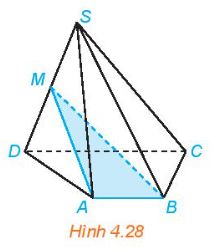
Lời giải

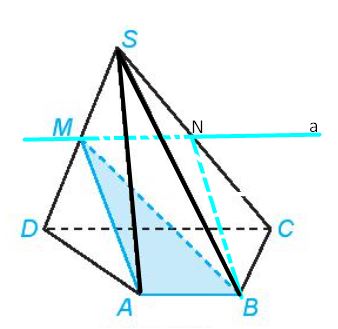
a) mp(MAB) và (SCD)có điểm M chung và chứa hai đường thẳng thẳng song song là AB và CD

Do đó giao tuyến của hai mặt phẳng (MAB) và (SCD) là đường thẳng a đi qua M và song song với CD, AB

b) Xét tam giác SCD ta có: M là trung điểm của SD, MN // CD suy ra MN là đường trung bình của tam giác SCD

Bài 4.14 trang 83 SGK Toán 11 Kết nối tri thức

Cho tứ diện ABCD. Gọi M, N làn lượt là trung điểm của các cạnh BC, CD và P là một điểm thuộc cạnh AC.

a) Xác định giao tuyến d của hai mặt phẳng (AMN) và (BPD)

b) Chứng minh rằng d song song với BD

Lời giải

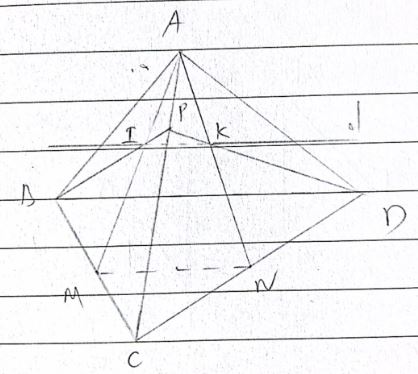
a) Gọi giao điểm của AM và BP là I, giao điểm của AN và DP là K

Ta có IK đều thuộc mặt phẳng (AMN) và (BPD) suy ra IK là giao tuyến của hai mặt phẳng này

Như vậy, d là đường thẳng đi qua I và K

b) Ta có: mp(AMN) ∩ mp(BPD) = IK

mp(AMN) ∩ mp(BCD) = MN

mp(BPD) ∩ mp(BCD) = BD

Mà MN // BD (do MN là đường trung bình của tam giác BCD) suy ra IK // BD

Như vây, d song song với BD

Bài 4.15 trang 83 SGK Toán 11 Kết nối tri thức

(Đố vui) Khi hai cánh cửa sổ hình chữ nhật được mở, dù ở vị trí nào, thì hai mép ngoài của chúng luôn song song với nhau (H.4.29). Hãy giải thích tại sao.

Nếu hai cánh cửa sổ có dạng hình thang như Hình 4.30 thì có vị trí nào của hai cánh cửa để hai mép ngoài của chúng song song với nhau hay không?

Lời giải

Bố sung sau

-------------------------

• Toán 11 Kết nối tri thức bài 12

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Kết nối tri thức bài 11: Hai đường thẳng song song. Mong rằng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 11 Kết nối tri thức. Mời các bạn cùng tham khảo thêm mục Ngữ văn 11 Kết nối tri thức.