Toán 11 Kết nối tri thức bài 23

Toán 11 Kết nối tri thức bài 23: Đường thẳng vuông góc với mặt được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo. Hi vọng qua đây bạn đọc có thêm tài liệu giải bài tập Toán 11 Kết nối tri thức. Mời các bạn cùng theo dõi bài viết dưới đây.

Bài 7.5 trang 36 SGK Toán 11 Kết nối

Cho hình chóp S.ABC có đáy là tam giác cân tại A và SA ⊥ (ABC). Gọi M là trung điểm của BC. Chứng minh rằng:

a) BC ⊥ (SAM);

b) Tam giác SBC cân tại S.

Bài làm

a) Ta có SA \(\perp\) (ABC) và AM là đường trung bình trong tam giác đều ABC, nên AM \(\perp\) BC và AM là đường cao của tam giác SBC. Khi đó, ta có BC \(\perp\) (SAM) vì BC \(\perp\) AM .

b) Ta có \(\widehat{ SBC} = 180^\circ -\widehat{ABC} = 180^\circ - \widehat{BAC} = \widehat{ SAC}\). Mặt khác, ta có SA = SC vì S là đỉnh của hình chóp S.ABC và AC là đường bờ của đáy ABC, vì ABC là tam giác cân tại A nên AC là đường trung trực của BC, suy ra SC = SA. Vậy SBC là tam giác cân tại S.

Bài 7.6 trang 36 SGK Toán 11 Kết nối

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA ⊥ (ABCD). Chứng minh rằng các mặt bên của hình chóp S.ABCD là các tam giác vuông.

Bài làm

Gọi M và N lần lượt là trung điểm của AB và CD. Khi đó, ta có MN // AD và MN // BC vì ABCD là hình chữ nhật.

Do đó, SM và SN là hai đường thẳng vuông góc với mặt phẳng (ABCD), và do đó chúng cũng vuông góc với tất cả các đường thẳng nằm trong mặt phẳng đó, bao gồm các cạnh AB, BC, CD và AD.

Vì SM ⊥ AB và SN ⊥ CD, nên SMB và SND là hai tam giác vuông. Tương tự, SMC và SNA cũng là hai tam giác vuông. Do đó, các mặt bên của hình chóp S.ABCD đều là các tam giác vuông.

Bài 7.7 trang 36 SGK Toán 11 Kết nối

Cho hình chóp S.ABCD có đáy là hình chữ nhật và SA ⊥ (ABCD). Gọi M, N tương ứng là hình chiếu của A trên SB, SD. Chứng minh rằng:

AM ⊥ (SBC), AN ⊥ (SCD), SC ⊥ (AMN).

Bài làm

Gọi O là trung điểm của AB, BC, CD và DA. Khi đó, SO là đường thẳng vuông góc với mặt phẳng (ABCD) và đi qua trung điểm O của đường chéo AC của hình chữ nhật.

Vì SA ⊥ (ABCD), nên SA ⊥ (ABCD), SA // SO. Do đó, SAOM là hình bình hành. Vì OM ⊥ SB, nên AM ⊥ SB. Tương tự, ta chứng minh được AN ⊥ SD.

Ta có SM//ND vì SM và ND cùng vuông góc với mặt phẳng (SBD) và đi qua cùng một điểm A. Vậy, \(\widehat{AMN\;}=\;\widehat{BMS}\;=\;\widehat{SBC}\). Như vậy, AM ⊥ (SBC). Tương tự, ta chứng minh được AN ⊥ (SCD).

Cuối cùng, ta chứng minh được SC ⊥ (AMN) như sau: Vì AM vuông góc với SB nên SC vuông góc với mặt phẳng (SAB). Tương tự, SC vuông góc với mặt phẳng (SCD). Do đó, SC là đường vuông góc chung của hai mặt phẳng (SAB) và (SCD), suy ra SC ⊥ (AMN).

Bài 7.8 trang 36 SGK Toán 11 Kết nối

Bạn Vinh thả quả dọi chìm vào thùng nước. Hỏi khi dây dọi căng và mặt nước yên lặng thì đường thẳng chứa dây dọi có vuông góc với mặt phẳng chứa mặt nước trong thùng hay không?

Bài 7.9 trang 36 SGK Toán 11 Kết nối

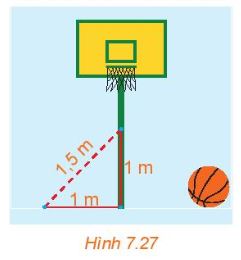
Một cột bóng rổ được dựng trên một sân phẳng. Bạn Hùng đo khoảng cách từ một điểm trên sân, cách chân cột 1 m đến một điểm trên cột, cách chân cột 1 m được kết quả là 1,5 m (H.7.27). Nếu phép đo của Hùng là chính xác thì cột có vuông góc với sân hay không? Có thể kết luận rằng cột không có phương thẳng đứng hay không?

---------------------------------

Bài tiếp theo: Toán 11 Kết nối tri thức bài 24

VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Kết nối tri thức bài 23: Đường thẳng vuông góc với mặt. Mong rằng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 11 Kết nối tri thức. Mời các bạn cùng tham khảo thêm tại mục Ngữ văn 11 Kết nối tri thức.