Toán 11 Chân trời sáng tạo bài 2 trang 136

Trung vị và tứ phân vị của mẫu số liệu ghép nhóm

Toán 11 Chân trời sáng tạo bài 2: Trung vị và tứ phân vị của mẫu số liệu ghép nhóm

Bài 1 trang 140 SGK Toán 11 Chân trời
Bài 2 trang 141 SGK Toán 11 Chân trời
Bài 3 trang 141 SGK Toán 11 Chân trời
Bài 4 trang 141 SGK Toán 11 Chân trời

VnDoc.com xin gửi tới bạn đọc bài viết Toán 11 Chân trời sáng tạo bài 2: Trung vị và tứ phân vị của mẫu số liệu ghép nhóm để bạn đọc cùng tham khảo và có thêm tài liệu giải bài tập Toán 11 Chân trời. Mời các bạn cùng theo dõi bài viết dưới đây.

Bài 1 trang 140 SGK Toán 11 Chân trời

Lương tháng của một số nhân viên văn phòng được ghi lại như sau (đơn vị: triệu đồng)

12,5	9,6	11,7	12,7	10,0	10,0	12,2	9,8	10,9	6,7	13,6	9,2
13,1	6,5	10,7	8,9	11,2	13,2	8,3	11,1	11,9	8,4	6,7	13,8

a) Tìm tứ phân vị của dãy số liệu trên

b) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:

Lương tháng (triệu đồng)	[6;8)	[8;10)	[10;12)	[12;14)
Số nhân viên	?	?	?	?

c) Hãy ước lượng tứ phân vị của số liệu ở bảng tần số ghép nhóm trên

Bài làm

a) Tứ phân vị thứ nhất là: 9,01

Tứ phân vị thứ hai là: 10,8

Tứ phân vị thứ ba là: 12,35

b)

Lương tháng (triệu đồng)	[6;8)	[8;10)	[10;12)	[12;14)
Số nhân viên	3	6	8	7

c) Gọi $x_{1};x_{2};x_{3};...;x_{24}$ $x_{1};x_{2};x_{3};...;x_{24}$ lần lượt là số nhân viên theo thứ tự không gian

Do $x_{1},...,x_{3} \in [6;8); x_{4},...,x_{9} \in [8;10);x_{10},...,x_{17} \in [10;12) ; x_{18},...,x_{24} \in [12;14)$ $x_{1},...,x_{3} \in [6;8); x_{4},...,x_{9} \in [8;10);x_{10},...,x_{17} \in [10;12) ; x_{18},...,x_{24} \in [12;14)$

Tứ phân vị thứ hai của dãy số liệu là $\frac{1}{2}(x_{12}+x_{13})$ $\frac{1}{2}(x_{12}+x_{13})$ thuộc nhóm [10;12) nên tứ phân vị thứ hai của mẫu số liệu là $Q_{2} = 10 + \frac{\frac{24}{2}-9}{8}(12-10) = 10,75$ $Q_{2} = 10 + \frac{\frac{24}{2}-9}{8}(12-10) = 10,75$

Tứ phân vị thứ nhất của dãy số liệu là $\frac{1}{2}(x_{6}+x_{7})$ $\frac{1}{2}(x_{6}+x_{7})$ thuộc nhóm [8;10) nên tứ phân vị thứ nhất của mẫu số liệu là $Q_{1} = 8 + \frac{\frac{24}{4}-3}{6}(10-8) = 9$ $Q_{1} = 8 + \frac{\frac{24}{4}-3}{6}(10-8) = 9$

Tứ phân vị thứ ba của dãy số liệu là $\frac{1}{2}(x_{18}+x_{19})$ $\frac{1}{2}(x_{18}+x_{19})$ thuộc nhóm [12;14) nên tứ phân vị thứ ba của mẫu số liệu là $Q_{3} = 12 + \frac{\frac{3.24}{4}-17}{7}(14-12) = 12,3$ $Q_{3} = 12 + \frac{\frac{3.24}{4}-17}{7}(14-12) = 12,3$

Bài 2 trang 141 SGK Toán 11 Chân trời

Số điểm một cầu thủ bóng rổ ghi được trong 20 trận đấu được cho ở bảng sau:

25	23	21	13	8	14	15	18	22	11
24	12	14	14	18	6	8	25	10	11

a) Tìm tứ phân vị của dãy số liệu trên

b) Tổng hợp lại dãy số liệu vào bảng tần số ghép nhóm theo mẫu sau:

Điểm số	[6;10]	[11;15]	[16;20]	[21;25]
Số trận	?	?	?	?

c) Hãy ước lượng phân vị của số liệu từ bảng tần số ghép nhóm trên

Bài làm

a) Tứ phân vị thứ nhất là: 11

Tứ phân vị thứ hai là: 14

Tứ phân vị thứ ba là: 21,5

b)

Điểm số	[6;10]	[11;15]	[16;20]	[21;25]
Số trận	3	9	2	6

c) Vì số trận là số nguyên nên ta hiệu chỉnh lại như sau:

Điểm số	[5,5;10,5)	[10,5;15,5)	[15,5;20,5)	[20,5;25,5)
Số trận	3	9	2	6

Gọi $x_{1};x_{2};x_{3};...;x_{20}$ $x_{1};x_{2};x_{3};...;x_{20}$ lần lượt là số trận theo thứ tự không gian

Do $x_{1},...,x_{3} \in [5,5;10,5); x_{4},...,x_{12} \in [10,5;15,5);x_{13},x_{14} \in [15,5;20,5) ; x_{15},...,x_{20} \in [20,5;25,5)$ $x_{1},...,x_{3} \in [5,5;10,5); x_{4},...,x_{12} \in [10,5;15,5);x_{13},x_{14} \in [15,5;20,5) ; x_{15},...,x_{20} \in [20,5;25,5)$

Tứ phân vị thứ hai của dãy số liệu là $\frac{1}{2}(x_{10}+x_{11})$ $\frac{1}{2}(x_{10}+x_{11})$ thuộc nhóm [10,5;15,5) nên tứ phân vị thứ hai của mẫu số liệu là $Q_{2} = 10,5 + \frac{\frac{20}{2}-3}{9}(15,5-10,5) = 14,4$ $Q_{2} = 10,5 + \frac{\frac{20}{2}-3}{9}(15,5-10,5) = 14,4$

Tứ phân vị thứ nhất của dãy số liệu là $\frac{1}{2}(x_{5}+x_{6})$ $\frac{1}{2}(x_{5}+x_{6})$ thuộc nhóm [10,5;15,5) nên tứ phân vị thứ nhất của mẫu số liệu là $Q_{1} = 10,5 + \frac{\frac{20}{4}-3}{9}(15,5-10,5) = 11,6$ $Q_{1} = 10,5 + \frac{\frac{20}{4}-3}{9}(15,5-10,5) = 11,6$

Tứ phân vị thứ ba của dãy số liệu là $\frac{1}{2}(x_{15}+x_{16})$ $\frac{1}{2}(x_{15}+x_{16})$ thuộc nhóm [20,5;25,5) nên tứ phân vị thứ ba của mẫu số liệu là $Q_{3} = 20,5 + \frac{\frac{3.20}{4}-14}{6}(25,5-20,5) = 21,3$ $Q_{3} = 20,5 + \frac{\frac{3.20}{4}-14}{6}(25,5-20,5) = 21,3$

Bài 3 trang 141 SGK Toán 11 Chân trời

Kiểm tra điện lượng của một số viên pin tiểu do một hãng sản xuất thu được kết quả sau:

Điện lượng (nghìn mAh)	[0,9;0,95)	[0,95;1,0)	[1,0;1,05)	[1,05;1,1)	[1,1;1,15)
Số viên pin	10	20	35	15	5

Hãy ước lượng số trung bình, mốt và tứ phân vị của mẫu số liệu ghép nhóm trên

Bài làm

Điện lượng (nghìn mAh)	[0,9;0,95)	[0,95;1,0)	[1,0;1,05)	[1,05;1,1)	[1,1;1,15)
Giá trị đại diện	0,925	0,975	1,025	1,075	1,125
Số viên pin	10	20	35	15	5

Số trung bình của dãy số liệu xấp xỉ bằng:

(0,925.10 + 0,975.20 + 1,025.35 + 1,075.15 + 1,125.5) : 85 = 1,016

Nhóm chứa mốt của dãy số liệu là: [1,0;1,05)

$M_{0} = 1,0 + \frac{35-20}{(35-20)+(35-15)}.(1,05-1,0) = 1,02$ $M_{0} = 1,0 + \frac{35-20}{(35-20)+(35-15)}.(1,05-1,0) = 1,02$

Gọi $x_{1};x_{2};x_{3};...;x_{85}$ $x_{1};x_{2};x_{3};...;x_{85}$ lần lượt là số viên pin theo thứ tự không gian

Do $x_{1},...,x_{10} \in [0,9;0,95); x_{11},...,x_{30} \in [0,95;1,0);x_{31},...,x_{65} \in [1,0;1,05) ; x_{66},...,x_{80} \in [1,05;1,1); x_{81},...,x_{85} \in [1,1;1,15)$ $x_{1},...,x_{10} \in [0,9;0,95); x_{11},...,x_{30} \in [0,95;1,0);x_{31},...,x_{65} \in [1,0;1,05) ; x_{66},...,x_{80} \in [1,05;1,1); x_{81},...,x_{85} \in [1,1;1,15)$

Tứ phân vị thứ hai của dãy số liệu là $\frac{1}{2}(x_{42}+x_{43})$ $\frac{1}{2}(x_{42}+x_{43})$ thuộc nhóm [1,0;1,05) nên tứ phân vị thứ hai của mẫu số liệu là $Q_{2} = 1,0 + \frac{\frac{85}{2}-30}{35}(1,05-1,0) = 1,02$ $Q_{2} = 1,0 + \frac{\frac{85}{2}-30}{35}(1,05-1,0) = 1,02$

Tứ phân vị thứ nhất của dãy số liệu là $\frac{1}{2}(x_{21}+x_{22})$ $\frac{1}{2}(x_{21}+x_{22})$ thuộc nhóm [0,95;1,0) nên tứ phân vị thứ nhất của mẫu số liệu là $Q_{1} = 0,95 + \frac{\frac{85}{4}-10}{20}(1,0-0,95) = 0,98$ $Q_{1} = 0,95 + \frac{\frac{85}{4}-10}{20}(1,0-0,95) = 0,98$

Tứ phân vị thứ ba của dãy số liệu là $\frac{1}{2}(x_{63}+x_{64})$ $\frac{1}{2}(x_{63}+x_{64})$ thuộc nhóm [1,0;1,05) nên tứ phân vị thứ ba của mẫu số liệu là $Q_{3} = 1,0 + \frac{\frac{3.85}{4}-30}{35}(1,05-1,0) = 1,048$ $Q_{3} = 1,0 + \frac{\frac{3.85}{4}-30}{35}(1,05-1,0) = 1,048$

Bài 4 trang 141 SGK Toán 11 Chân trời

Cân nặng của một con lợn con mới sinh thuộc hai giống A và B được cho ở biểu đồ dưới đây (đơn vị: kg)

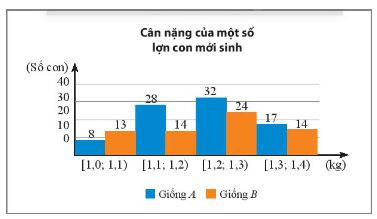
Toán 11 Chân trời sáng tạo bài 2

a) Hãy so sánh cân nặng của lớn con mới sinh giống A và giống B theo số trung bình và trung vị

b) Hãy ước lượng tứ phân vị thứ nhất và thứ ba của cân nặng lợn con mới sinh giống A và của cân nặng lợn con mới sinh giống B

--------------------------

Bài tiếp theo: Toán 11 Chân trời sáng tạo bài tập cuối chương 5

VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Chân trời sáng tạo bài 2: Trung vị và tứ phân vị của mẫu số liệu ghép nhóm. Hi vọng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 11 Chân trời sáng tạo. Mời các bạn cùng tham khảo thêm tại mục Ngữ văn 11 Chân trời sáng tạo.

Chia sẻ, đánh giá bài viết

1

152

Bài trước

Bài sau