Toán 11 Chân trời sáng tạo bài tập cuối chương 9

VnDoc.com xin gửi tới bạn đọc bài viết Toán 11 Chân trời sáng tạo bài tập cuối chương 9: Xác suất để bạn đọc cùng tham khảo và có thêm tài liệu giải bài tập Toán 11 Chân trời sáng tạo nhé.

Bài 1 trang 98 SGK Toán 11 Chân trời

Gieo 2 con xúc xắc cân đối và đồng chất. Gọi A là biến cố "Tích số chấm xuất hiện là số lẻ". Biến cố nào sau đây xung khắc với biến cố A?

A. "Xuất hiện 2 mặt có cùng số chấm"

B. "Tổng số chấm xuất hiện là số lẻ"

C. "Xuất hiện ít nhất một mặt có số chấm là số lẻ"

D. "Xuất hiện hai mặt có số chấm khác nhau"

Bài làm

Đáp án B

Bài 2 trang 98 SGK Toán 11 Chân trời

Cho A và B là hai biến cố độc lập. Biết P(A) = 0,4 và P(B) = 0,5. Xác suất của biến cố A ∪ B là:

A. 0,9

B. 0,7

C. 0,5

D. 0,2

Bài làm

Đáp án B

Bài 3 trang 98 SGK Toán 11 Chân trời

Gieo 2 con xúc xắc cân đối và đồng chất. Xác suất của biến cố "Tổng số chấm xuất hiện trên hai con xúc xắc chia hết cho 5" là:

A. \(\frac{5}{36}\)

B. \(\frac{1}{6}\)

C. \(\frac{7}{36}\)

D. \(\frac{2}{9}\)

Bài làm

Đáp án C

Bài 4 trang 98 SGK Toán 11 Chân trời

Lấy ra ngẫu nhiên 2 quả bóng từ một hộp chứa 5 quả bóng xanh và 4 quả bóng đỏ có kích thước và khối lượng như nhau. Xác suất của biến cố "Hai bóng lấy ra có cùng màu" là:

A. \(\frac{1}{9}\)

B. \(\frac{2}{9}\)

C. \(\frac{4}{9}\)

D. \(\frac{5}{9}\)

Bài làm

Đáp án C

Bài 5 trang 98 SGK Toán 11 Chân trời

Chọn ngẫu nhiên 2 đỉnh của một hình bát giác đều nội tiếp trong đường tròn tâm O bán kính R. Xác suất để khoảng cách giữa hai đỉnh đó bằng R\(\sqrt{2}\) là:

A. \(\frac{2}{7}\)

B. \(\frac{3}{7}\)

C. \(\frac{4}{7}\)

D. \(\frac{5}{56}\)

Bài làm

Đáp án A

Bài 6 trang 98 SGK Toán 11 Chân trời

Cho A và B là hai biến cố thoả mãn P(A) = 0,5; P(B) = 0,7 và P(A ∪ B) = 0,8

a) Tính xác suất của các biến cố AB, \(\bar{A}\)B và \(\bar{A} \bar{B}\)

b) Hai biến cố A và B có độc lập hay không

Bài làm

a) P(A ∪ B) = P(A) + P(B) − P(AB). Suy ra P(AB) = 0,4

P(\(\bar{A}\)B) = P(B) − P(AB) = 0,7 − 0,4 = 0,3

P(\(\bar{A} \bar{B}\)) = 1 − P(A ∪ B) = 0,2

b) Vì P(AB) ≠ P(A).P(B) nên A và B không độc lập

Bài 7 trang 98 SGK Toán 11 Chân trời

Vệ tinh A lần lượt truyền một tin đến vệ tính B cho đến khi vệ tinh B phản hồi là đã nhận được. Biết khả năng vệ tinh B phản hồi đã nhận được tin ở mỗi lần A gửi là độc lập với nhau và xác suất phản hồi mỗi lần đều là 0,4. Sử dụng sơ đồ hình cây, tính xác suất vệ tinh A phải gửi tin không quá 3 lần

Bài làm

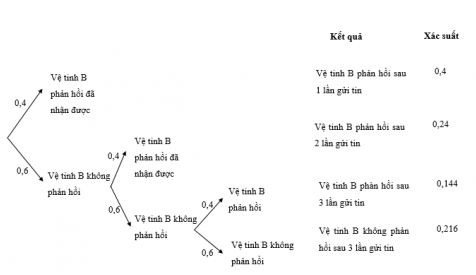
Nhìn vào sơ đồ ta thấy xác suất vệ tính A phải gửi tin không quá 3 lần là: 0,4 + 0,24 + 0,144 = 0,784

Bài 8 trang 98 SGK Toán 11 Chân trời

Gieo 2 con xúc xắc cân đối và đồng chất. Tính xác suất của biến cố "Tích số chấm xuất hiện trên hai con xúc xắc chia hết cho 6"

Bài làm

A là biến cố "Có 1 số chấm chia hết cho 2, 1 số chấm chia hết cho 3, và không xuất hiện 6 chấm", P(A) = \(\frac{4}{36}\) = \(\frac{1}{9}\)

B là biến cố "Có ít nhất 1 trong 2 con xúc xắc xuất hiện chấm 6", P(B) = \(\frac{11}{36}\)

A∪B là biến cố "Tích số chấm xuất hiện trên 2 con xúc xắc chia hết cho 6".

A và B xung khắc nên P(A ∪ B) = P(A) + P(B) = \(\frac{5}{12}\)

Bài 9 trang 98 SGK Toán 11 Chân trời

Một hộp có 5 quả bóng xanh, 6 quả bóng đỏ và 4 quả bóng vàng có kích thước và khối lượng như nhau. Chọn ra ngẫu nhiên từ hộp 4 quả bóng. Tính xác suất của các biến cố:

A: "Cả 4 quả bóng lấy ra có cùng màu"

B: "Trong 4 quả bóng lấy ra có đủ cả 3 màu"

Bài làm

a) \(A_{1}\) là biến cố cả 4 quả bóng lấy ra đều có màu xanh; \(P(A_{1}) = \frac{C_{5}^{4}}{C_{15}^{4}}\)

\(A_{2}\) là biến cố cả 4 quả bóng lấy ra đều có màu đỏ; \(P(A_{2}) = \frac{C_{6}^{4}}{C_{15}^{4}}\)

\(A_{3}\) là biến cố cả 4 quả bóng lấy ra đều có màu vàng; \(P(A_{3}) = \frac{C_{4}^{4}}{C_{15}^{4}}\)

Khi đó, \(A = A_{1} \cup A_{2} \cup A_{3}\)

Mà \(A_{1}, A_{2}, A_{3}\) là các biến cố xung khắc nên

\(P(A) = P(A_{1}) + P(A_{2}) +P(A_{3}) = \frac{1}{65}\)

b) \(B_{1}\) là biến cố có 2 quả bóng xanh, 1 quả bóng đỏ, 1 quả bóng vàng; \(P(B_{1}) = \frac{C_{5}^{2}.C_{6}^{1}.C_{4}^{1}}{C_{15}^{4}}\)

\(B_{2}\) là biến cố có 1 quả bóng xanh, 2 quả bóng đỏ, 1 quả bóng vàng; \(P(B_{2}) = \frac{C_{5}^{1}.C_{6}^{2}.C_{4}^{1}}{C_{15}^{4}}\)

B_{3} là biến cố có 1 quả bóng xanh, 1 quả bóng đỏ, 2 quả bóng vàng; \(P(B_{1}) = \frac{C_{5}^{1}.C_{6}^{1}.C_{4}^{2}}{C_{15}^{4}}\)

Khi đó, \(B = B_{1} \cup B_{2} \cup B_{3}\)

Mà \(B_{1}, B_{2}, B_{3}\) là các biến cố xung khắc nên

\(P(B) = P(B_{1}) + P(B_{2}) +P(B_{3}) = \frac{48}{91}\)

Bài 10 trang 98 SGK Toán 11 Chân trời

Cường, Trọng và 6 bạn nữ xếp ngẫu nhiên thành một hàng ngang để chụp ảnh. Tính xác suất của biến cố "Có ít nhất một trong hai bạn Cường và Trọng đứng ở đầu hàng"

Bài làm

A là biến cố "Cường đứng đầu hàng", P(A) =\frac{6!.C_{2}^{1}}{7!} = \frac{2}{7}

B là biến cố "Trọng đứng đầu hàng", P(B) =\frac{6!.C_{2}^{1}}{7!} = \frac{2}{7}

AB là biến cố "Trọng và Cường cùng đứng đầu hàng" P(AB) = \frac{2!.5!}{7!} = \frac{1}{21}

A \cup B là biến cố "Có ít nhất một trong hai bạn Cường và Trọng đứng ở đầu hàng"

P(A \cup B) = P(A) + P(B) -P(A).P(B) = \frac{11}{21}

Bài 11 trang 98 SGK Toán 11 Chân trời

Chọn ngẫu nhiên 3 trong số 24 đỉnh của một đa giác đều 24 cạnh. Tính xác suất của biến cố "3 đỉnh được chọn là 3 đỉnh của một tam giác cân hoặc một tam giác vuông"

Bài 12 trang 98 SGK Toán 11 Chân trời

Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên có 3 chữ số. Tính xác suất của các biến cố:

A: "Số được chọn chia hết cho 2 hoặc 7"

B: "Số được chọn có tổng các chữ số là số chắn"

Bài 13 trang 98 SGK Toán 11 Chân trời

Cho hai giống cá kiếm mắt đen thuần chủng và mắt đỏ thuần chủng giao phối với nhau được F1 toàn cá kiếm mắt đen. Lại cho cả F1 giao phối với nhau được một đàn cá con mới. Chọn ra ngẫu nhiên 2 con trong đàn cá con mới. Ước lượng xác suất biến cố "Có ít nhất 1 con cá mắt đen trong 2 con cá đó"

---------------------------------

Bài tiếp theo: Toán 11 Chân trời sáng tạo bài 1: Vẽ hình khối bằng phần mềm GeoGebra. Làm kính 3D để quan sát ảnh nổi

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Chân trời sáng tạo bài tập cuối chương 9: Xác suất. Mong rằng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 11 Chân trời sáng tạo. Mời các bạn cùng tham khảo thêm tại mục Ngữ văn 11 Chân trời sáng tạo.