Toán 11 Chân trời sáng tạo bài 1 trang 45

Dãy số

Toán 11 Chân trời sáng tạo bài 1: Dãy số

Bài 1 trang 50 SGK Toán 11 Chân trời
Bài 2 trang 50 SGK Toán 11 Chân trời
Bài 3 trang 50 SGK Toán 11 Chân trời
Bài 4 trang 50 SGK Toán 11 Chân trời
Bài 5 trang 50 SGK Toán 11 Chân trời
Bài 6 trang 50 SGK Toán 11 Chân trời
Bài 7 trang 50 SGK Toán 11 Chân trời

Toán 11 Chân trời sáng tạo bài 1: Dãy số được VnDoc.com tổng hợp và xin gửi tới bạn đọc cùng tham khảo. Hi vọng qua bài viết này bạn đọc có thêm tài liệu để giải bài tập Toán 11 Chân trời sáng tạo nhé. Mời các bạn cùng theo dõi bài viết dưới đây.

Bài 1 trang 50 SGK Toán 11 Chân trời

Tìm $u_{2}, u_{3}$ $u_{2}, u_{3}$ và dự đoán công thức số hạng tổng quát $u_{n}$ $u_{n}$ của dãy số:

$\left\{\begin{matrix}u_{1}=1\\u_{n+1}=\frac{u_{n}}{1+u_{n}} (n\geq 1)\end{matrix}\right.$ $\left\{\begin{matrix}u_{1}=1\\u_{n+1}=\frac{u_{n}}{1+u_{n}} (n\geq 1)\end{matrix}\right.$

Lời giải

$u_{2}= \frac{1}{2}; u_{3}= \frac{1}{3}$ $u_{2}= \frac{1}{2}; u_{3}= \frac{1}{3}$

$u_{n}=\frac{1}{n}$ $u_{n}=\frac{1}{n}$

Bài 2 trang 50 SGK Toán 11 Chân trời

Cho dãy số $(u_{n}) với u_{n}=\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{n(n+1)}$ $(u_{n}) với u_{n}=\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{n(n+1)}$. Tìm $u_{1}, u_{2}, u_{3}$ $u_{1}, u_{2}, u_{3}$ và dự đoán công thức số hạng tổng quát $u_{n}$ $u_{n}$

Lời giải

$u_{1}= \frac{1}{2}; u_{2}=\frac{2}{3}; u_{3} = \frac{3}{4}$ $u_{1}= \frac{1}{2}; u_{2}=\frac{2}{3}; u_{3} = \frac{3}{4}$

$u_{n}= \frac{n}{n+1}$ $u_{n}= \frac{n}{n+1}$

Bài 3 trang 50 SGK Toán 11 Chân trời

Xét tính tăng, giảm của dãy số $(y_{n}) với y_{n}=\sqrt{n+1}-\sqrt{n}$ $(y_{n}) với y_{n}=\sqrt{n+1}-\sqrt{n}$

Lời giải

Ta có:

$y_{n} = \sqrt{n+1}-\sqrt{n} = \frac{(\sqrt{n+1}-\sqrt{n}).(\sqrt{n+1}+\sqrt{n})}{\sqrt{n+1}+\sqrt{n}} = \frac{1}{\sqrt{n+1}+\sqrt{n}}$ $y_{n} = \sqrt{n+1}-\sqrt{n} = \frac{(\sqrt{n+1}-\sqrt{n}).(\sqrt{n+1}+\sqrt{n})}{\sqrt{n+1}+\sqrt{n}} = \frac{1}{\sqrt{n+1}+\sqrt{n}}$

$y_{n+1} = \frac{1}{\sqrt{n+2}+\sqrt{n+1}}$ $y_{n+1} = \frac{1}{\sqrt{n+2}+\sqrt{n+1}}$

$\forall n \in N* , y_{n+1} < y_{n}$ $\forall n \in N* , y_{n+1} < y_{n}$

Vậy dãy số $(y_{n})$ $(y_{n})$ là dãy số giảm

Bài 4 trang 50 SGK Toán 11 Chân trời

Xét tính bị chặn của các dãy số sau:

a) $(a_{n}) với a_{n}=sin^{2}\frac{n\pi }{3}+cos\frac{n\pi }{4}$ $(a_{n}) với a_{n}=sin^{2}\frac{n\pi }{3}+cos\frac{n\pi }{4}$

b) $(u_{n}) với u_{n}=\frac{6n-4}{n+2}$ $(u_{n}) với u_{n}=\frac{6n-4}{n+2}$

Lời giải

a) $\forall n\in \mathbb{N}^{*}$ $\forall n\in \mathbb{N}^{*}$, Ta có:

$0\leq sin^{2}\frac{n\pi }{3} \leq 1$ $0\leq sin^{2}\frac{n\pi }{3} \leq 1$

$-1\leq cos\frac{n\pi }{4} \leq 1$ $-1\leq cos\frac{n\pi }{4} \leq 1$

Suy ra $- 1\leq a_{n} \leq 2$ $- 1\leq a_{n} \leq 2$

Vậy dãy số $(a_{n})$ $(a_{n})$ bị chặn

b) $u_{n}=\frac{6n-4}{n+2} = 6 -\frac{16}{n+2}$ $u_{n}=\frac{6n-4}{n+2} = 6 -\frac{16}{n+2}$

$u_{n} < 6, \forall n\in \mathbb{N}^{*}$ $u_{n} < 6, \forall n\in \mathbb{N}^{*}$. Vậy dãy số $(u_{n})$ $(u_{n})$ bị chặn trên

$u_{n} >-2, \forall n\in \mathbb{N}^{*}$ $u_{n} >-2, \forall n\in \mathbb{N}^{*}$. Vậy dãy số $(u_{n})$ $(u_{n})$ bị chặn dưới

Suy ra, dãy số $(u_{n})$ $(u_{n})$ bị chặn

Bài 5 trang 50 SGK Toán 11 Chân trời

Cho dãy số $(u_{n}) với u_{n}=\frac{2n-1}{n+1}$ $(u_{n}) với u_{n}=\frac{2n-1}{n+1}$

Chứng minh $(u_{n})$ $(u_{n})$ là dãy số tăng và bị chặn

Lời giải

$u_{n}=\frac{2n-1}{n+1} = 2 - \frac{3}{n+1}$ $u_{n}=\frac{2n-1}{n+1} = 2 - \frac{3}{n+1}$

Ta có $\forall n\in \mathbb{N}^{*}, u_{n+1}=2 - \frac{3}{n+2}> u_{n} = 2 - \frac{3}{n+1}$ $\forall n\in \mathbb{N}^{*}, u_{n+1}=2 - \frac{3}{n+2}> u_{n} = 2 - \frac{3}{n+1}$

Vậy dãy số $(u_{n})$ $(u_{n})$ là dãy số tăng

$u_{n}= 2 - \frac{3}{n+1} > -1, \forall n\in \mathbb{N}^{*}$ $u_{n}= 2 - \frac{3}{n+1} > -1, \forall n\in \mathbb{N}^{*}$. Vậy dãy số $(u_{n})$ $(u_{n})$ bị chặn dưới

$u_{n}= 2 - \frac{3}{n+1} < 2, \forall n\in \mathbb{N}^{*}$ $u_{n}= 2 - \frac{3}{n+1} < 2, \forall n\in \mathbb{N}^{*}$. Vậy dãy số $(u_{n})$ $(u_{n})$ bị chặn trên

Suy ra dãy số $(u_{n})$ $(u_{n})$ bị chặn

Bài 6 trang 50 SGK Toán 11 Chân trời

Cho dãy số $(u_{n}) với u_{n}=\frac{na+2}{n+1}$ $(u_{n}) với u_{n}=\frac{na+2}{n+1}$. Tìm giá trị của a để:

a) $(u_{n})$ $(u_{n})$ là dãy số tăng

b) $(u_{n})$ $(u_{n})$ là dãy số giảm

Lời giải

a) $(u_{n})$ $(u_{n})$ là dãy số tăng khi $\forall x \in \mathbb{N}^{*} thì: u_{n+1}>u_{n}$ $\forall x \in \mathbb{N}^{*} thì: u_{n+1}>u_{n}$

$\Leftrightarrow \frac{(n+1)a+2}{n+1+1}>\frac{na+2}{n+1}; \forall x \in \mathbb{N}^{*}$ $\Leftrightarrow \frac{(n+1)a+2}{n+1+1}>\frac{na+2}{n+1}; \forall x \in \mathbb{N}^{*}$

$\Leftrightarrow a+\frac{2-a}{n+2}>a+\frac{2-a}{n+1}; \forall x \in \mathbb{N}^{*}$ $\Leftrightarrow a+\frac{2-a}{n+2}>a+\frac{2-a}{n+1}; \forall x \in \mathbb{N}^{*}$

$\Leftrightarrow \frac{2-a}{n+2}>\frac{2-a}{n+1}; \forall x \in \mathbb{N}^{*}$ $\Leftrightarrow \frac{2-a}{n+2}>\frac{2-a}{n+1}; \forall x \in \mathbb{N}^{*}$

$\Leftrightarrow 2-a <0$ $\Leftrightarrow 2-a <0$

$\Leftrightarrow a>2$ $\Leftrightarrow a>2$

b) $(u_{n})$ $(u_{n})$ là dãy số tăng khi $\forall x \in \mathbb{N}^{*}$ $\forall x \in \mathbb{N}^{*}$ thì: $u_{n+1} < u_{n}$ $u_{n+1} < u_{n}$

$\Leftrightarrow \frac{(n+1)a+2}{n+1+1}<\frac{na+2}{n+1}; \forall x \in \mathbb{N}^{*}$ $\Leftrightarrow \frac{(n+1)a+2}{n+1+1}<\frac{na+2}{n+1}; \forall x \in \mathbb{N}^{*}$

$\Leftrightarrow a+\frac{2-a}{n+2}< a+\frac{2-a}{n+1}; \forall x \in \mathbb{N}^{*}$ $\Leftrightarrow a+\frac{2-a}{n+2}< a+\frac{2-a}{n+1}; \forall x \in \mathbb{N}^{*}$

$\Leftrightarrow \frac{2-a}{n+2}<\frac{2-a}{n+1}; \forall x \in \mathbb{N}^{*}$ $\Leftrightarrow \frac{2-a}{n+2}<\frac{2-a}{n+1}; \forall x \in \mathbb{N}^{*}$

$\Leftrightarrow 2-a >0$ $\Leftrightarrow 2-a >0$

$\Leftrightarrow a<2$ $\Leftrightarrow a<2$

Bài 7 trang 50 SGK Toán 11 Chân trời

Trên lưới ô vuông, mỗi ô cạnh 1 đơn vị, người ta vẽ 8 hình vuông và tô màu khác nhau như Hình 3. Tìm dãy số biểu diễn độ dài cạnh của 8 hình vuông đó từ nhỏ đến lớn. Có nhận xét gì về dãy số trên?

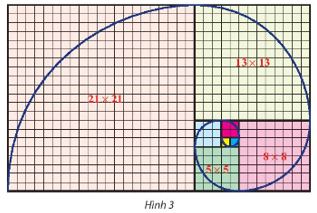
Toán 11 Chân trời sáng tạo bài 1: Dãy số

Lời giải

$u_{1}=1; u_{2}=1; u_{3}=2; u_{4}=3; u_{5}=5; u_{6}=8; u_{7}=13; u_{8}=21$ $u_{1}=1; u_{2}=1; u_{3}=2; u_{4}=3; u_{5}=5; u_{6}=8; u_{7}=13; u_{8}=21$

Ta có dãy số $(u_{n}) : \left\{\begin{matrix}u_{1}=1\\ u_{2}=1\\u_{n} = u_{n-1}+u_{n-2}\end{matrix}\right.$ $(u_{n}) : \left\{\begin{matrix}u_{1}=1\\ u_{2}=1\\u_{n} = u_{n-1}+u_{n-2}\end{matrix}\right.$

------------------

Toán 11 Chân trời sáng tạo Bài 2

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Chân trời sáng tạo bài 1: Dãy số. Mong rằng qua đây bạn đọc có thể học tập tốt hơn môn Toán 11 Chân trời sáng tạo nhé.

Chia sẻ, đánh giá bài viết

1

119

Bài trước

Bài sau