Toán 11 Chân trời sáng tạo bài 3 trang 80

Hàm số liên tục

Toán 11 Chân trời sáng tạo bài 3: Hàm số liên tục

Bài 1 trang 84 SGK Toán 11 Chân trời
Bài 2 trang 84 SGK Toán 11 Chân trời
Bài 3 trang 85 SGK Toán 11 Chân trời
Bài 4 trang 85 SGK Toán 11 Chân trời
Bài 5 trang 85 SGK Toán 11 Chân trời
Bài 6 trang 85 SGK Toán 11 Chân trời

VnDoc.com xin gửi tới bạn đọc bài viết Toán 11 Chân trời sáng tạo bài 3: Hàm số liên tục để bạn đọc cùng tham khảo và có thêm tài liệu giải bài tập Toán 11 Chân trời sáng tạo nhé. Mời các bạn cùng theo dõi bài viết dưới đây.

Bài 1 trang 84 SGK Toán 11 Chân trời

Xét tính liên tục của hàm số:

a) $f(x)=\left\{\begin{matrix}x^{2}+1; x \geq 0\\1-x; x<0\end{matrix}\right.$ $f(x)=\left\{\begin{matrix}x^{2}+1; x \geq 0\\1-x; x<0\end{matrix}\right.$ tại điểm x = 0

b) $f(x)=\left\{\begin{matrix}x^{2}+2; x \geq1\\ x; x<1\end{matrix}\right.$ $f(x)=\left\{\begin{matrix}x^{2}+2; x \geq1\\ x; x<1\end{matrix}\right.$ tại điểm x = 1

Lời giải

a) $\lim_{x \to 0^{-}}f(x)=\lim_{x \to 0^{-}}(1-x)=1-0=1$ $\lim_{x \to 0^{-}}f(x)=\lim_{x \to 0^{-}}(1-x)=1-0=1$

$\lim_{x \to 0^{+}}f(x)=\lim_{x \to 0^{+}}(x^{2}+1)=0^{2}+1=1$ $\lim_{x \to 0^{+}}f(x)=\lim_{x \to 0^{+}}(x^{2}+1)=0^{2}+1=1$

Suy ra: $\lim_{x \to 0}f(x)= f(0)$ $\lim_{x \to 0}f(x)= f(0)$

Vậy hàm số y = f(x) liên tục tại x = 0

b) $\lim_{x \to 1^{-}}f(x)=\lim_{x \to 1^{-}}x=1$ $\lim_{x \to 1^{-}}f(x)=\lim_{x \to 1^{-}}x=1$

$\lim_{x \to 1^{+}}f(x)=\lim_{x \to 1^{+}}(x^{2}+2)=1^{2}+2=3$ $\lim_{x \to 1^{+}}f(x)=\lim_{x \to 1^{+}}(x^{2}+2)=1^{2}+2=3$

Suy ra không tồn tại $\lim_{x \to 1}f(x)$ $\lim_{x \to 1}f(x)$

Vậy hàm số y = f(x) không liên tục tại x = 1

Bài 2 trang 84 SGK Toán 11 Chân trời

Cho hàm số $\left\{\begin{matrix}\frac{x^{2}-4}{x+2}; x \neq -2\\ a; x=-2\end{matrix}\right.$ $\left\{\begin{matrix}\frac{x^{2}-4}{x+2}; x \neq -2\\ a; x=-2\end{matrix}\right.$

Tìm a để hàm số y = f(x) liên tục trên $\mathbb{R}$ $\mathbb{R}$

Lời giải

Ta có: $\lim_{x \to -2}f(x)=\lim_{x \to -2}\frac{x^{2}-4}{x+2} = \lim_{x \to -2}\frac{(x-2)(x+2)}{x+2} =\lim_{x \to -2}(x-2)=-2-2=-4$ $\lim_{x \to -2}f(x)=\lim_{x \to -2}\frac{x^{2}-4}{x+2} = \lim_{x \to -2}\frac{(x-2)(x+2)}{x+2} =\lim_{x \to -2}(x-2)=-2-2=-4$

f(-2) = a

Để hàm số f(x) liên tục trên $\mathbb{R}$ $\mathbb{R}$ thì hàm số f(x) phải liên tục tại $x_{0}=-2$ $x_{0}=-2$

Hay $\lim_{x \to -2}f(x) = f(-2)$ $\lim_{x \to -2}f(x) = f(-2)$

Suy ra: a = -4

Bài 3 trang 85 SGK Toán 11 Chân trời

Xét tính liên tục của hàm số sau:

a) $f(x) = \frac{x}{x^{2}-4}$ $f(x) = \frac{x}{x^{2}-4}$

b) $g(x) = \sqrt{9-x^{2}}$ $g(x) = \sqrt{9-x^{2}}$

c) $h(x) = cosx + tanx$

Lời giải

a) $f(x) = \frac{x}{x^{2}-4}$ $f(x) = \frac{x}{x^{2}-4}$ là hàm số phân thức có tập xác định là $(-\infty;2) \cup (2;+\infty)$ $(-\infty;2) \cup (2;+\infty)$

Nên hàm số f(x) liên tục trên các khoảng $(-\infty;2) và (2;+\infty)$ $(-\infty;2) và (2;+\infty)$

b) $g(x) = \sqrt{9-x^{2}}$ $g(x) = \sqrt{9-x^{2}}$ là hàm số căn thức có tập xác định là [-3;3] nên hàm só g(x) liên tục trên đoạn [-3;3]

c) h(x) = cosx + tanx là hàm số lượng giác có tập xác định là $\mathbb{R} \ { \frac{\pi}{2} + k\pi }$ $\mathbb{R} \ { \frac{\pi}{2} + k\pi }$

Nên hàm số h(x) liên tục trên các khoảng $\mathbb{R} \ { \frac{\pi}{2} + k\pi }$ $\mathbb{R} \ { \frac{\pi}{2} + k\pi }$

Bài 4 trang 85 SGK Toán 11 Chân trời

Cho hàm số f(x) = 2x -sinx , g(x) = $\sqrt{x-1}$ $\sqrt{x-1}$

Xét tính liên tục hàm số $y = f(x).g(x) và y = \frac{f(x)}{g(x)}$ $y = f(x).g(x) và y = \frac{f(x)}{g(x)}$

Lời giải

Hàm số f(x) = 2x - sinx liên tục với mọi $x \in \mathbb{R}$ $x \in \mathbb{R}$

Hàm số $g(x) = \sqrt{x-1}$ $g(x) = \sqrt{x-1}$ liên tục trên khoảng $[1;+\infty)$ $[1;+\infty)$

Suy ra: hàm số $y=f(x).g(x)$ liên tục trên khoảng $[1;+\infty)$ $[1;+\infty)$

$g(x) \neq 0$ $g(x) \neq 0$ khi $x \neq 1$ $x \neq 1$

Suy ra hàm số $y=\frac{f(x)}{g(x)}$ $y=\frac{f(x)}{g(x)}$ liên tục trên khoảng $(1;+\infty)$ $(1;+\infty)$

Bài 5 trang 85 SGK Toán 11 Chân trời

Một bãi đậu xe ô tô đưa ra giá C(x) (đồng) khi thời gian đậu xe là x (giờ) như sau:

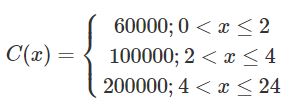
Toán 11 Chân trời sáng tạo bài 3

Xét tính liên tục của hàm số C(x).

Lời giải

C(x) = 60000 khi $x \in (0;2)$ $x \in (0;2)$ nên hàm số C(x) liên tục trên (0;2)

C(x) = 100000 khi $x \in (2;4)$ $x \in (2;4)$ nên hàm số C(x) liên tục trên (2;4)

C(x) = 200000 khi $x \in (4;24)$ $x \in (4;24)$ nên hàm số C(x) liên tục trên (4;24)

Ta có:

$\lim_{x \to 2^{-}}C(x)= 60000$ $\lim_{x \to 2^{-}}C(x)= 60000$

$\lim_{x \to 2^{+}}C(x)= 100000$ $\lim_{x \to 2^{+}}C(x)= 100000$

Vậy không tồn tại $\lim_{x \to 2}$ $\lim_{x \to 2}$ hay hàm số C(x) không liên tục tại 2

$\lim_{x \to 4^{-}}C(x)= 100000$ $\lim_{x \to 4^{-}}C(x)= 100000$

$\lim_{x \to 4^{+}}C(x)= 200000$ $\lim_{x \to 4^{+}}C(x)= 200000$

Vậy không tồn tại $\lim_{x \to 4}$ $\lim_{x \to 4}$ hay hàm số C(x) không liên tục tại 4

Bài 6 trang 85 SGK Toán 11 Chân trời

Lực hấp dẫn do Trái đất tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm của nó là:

$F(r)=\left\{\begin{matrix} \frac{GMr}{R^{3}}; 0 < r < R\\ \frac{GM}{r^{2}}; r\geq R\end{matrix}\right.$ $F(r)=\left\{\begin{matrix} \frac{GMr}{R^{3}}; 0 < r < R\\ \frac{GM}{r^{2}}; r\geq R\end{matrix}\right.$

Trong đó M là khối lương, R là bán kính của Trái đất, G là hằng số hấp dẫn. Hàm số F(r) có liên tục trên $(0;+\infty)$ $(0;+\infty)$ không?

Lời giải

$\lim_{r \to R^{-}}F(r)=\lim_{r \to R^{-}}\frac{GMr}{R^{3}}=\frac{GMR}{R^{3}}=\frac{GM}{R^{2}}$ $\lim_{r \to R^{-}}F(r)=\lim_{r \to R^{-}}\frac{GMr}{R^{3}}=\frac{GMR}{R^{3}}=\frac{GM}{R^{2}}$

$\lim_{r \to R^{+}}F(r)=\lim_{r \to R^{+}}\frac{GM}{r^{2}}=\frac{GM}{R^{2}}$ $\lim_{r \to R^{+}}F(r)=\lim_{r \to R^{+}}\frac{GM}{r^{2}}=\frac{GM}{R^{2}}$

Suy ra: $\lim_{r \to R}F(r) = F(R)$ $\lim_{r \to R}F(r) = F(R)$. Hay hàm số F(r) liên tục tại $r_{0} = R$ $r_{0} = R$

$F(r)= \frac{GMr}{R^{3}} khi 0 < r < R$ $F(r)= \frac{GMr}{R^{3}} khi 0 < r < R$ nên hàm F(r) liên tục trên (0;R)

$F(r)= \frac{GM}{r^{3}}$ $F(r)= \frac{GM}{r^{3}}$ khi r > R nên hàm F(r) liên tục trên $(R;+\infty)$ $(R;+\infty)$

Vậy hàm số F(r) liên tục trên $(0;+\infty)$ $(0;+\infty)$

------------------------------

Bài tiếp theo: Toán 11 Chân trời sáng tạo bài tập cuối chương 3

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Chân trời sáng tạo bài 3: Hàm số liên tục. Mong rằng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 11 Chân trời sáng tạo nhé.

Chia sẻ, đánh giá bài viết

1

132

Bài trước

Bài sau