VnDoc.com

Đề thi thử Toán (chung) vào 10 chuyên năm 2024 - 2025 phòng GD&ĐT TP Nam Định

Đề thi tuyển sinh lớp 10 môn Toán có đáp án

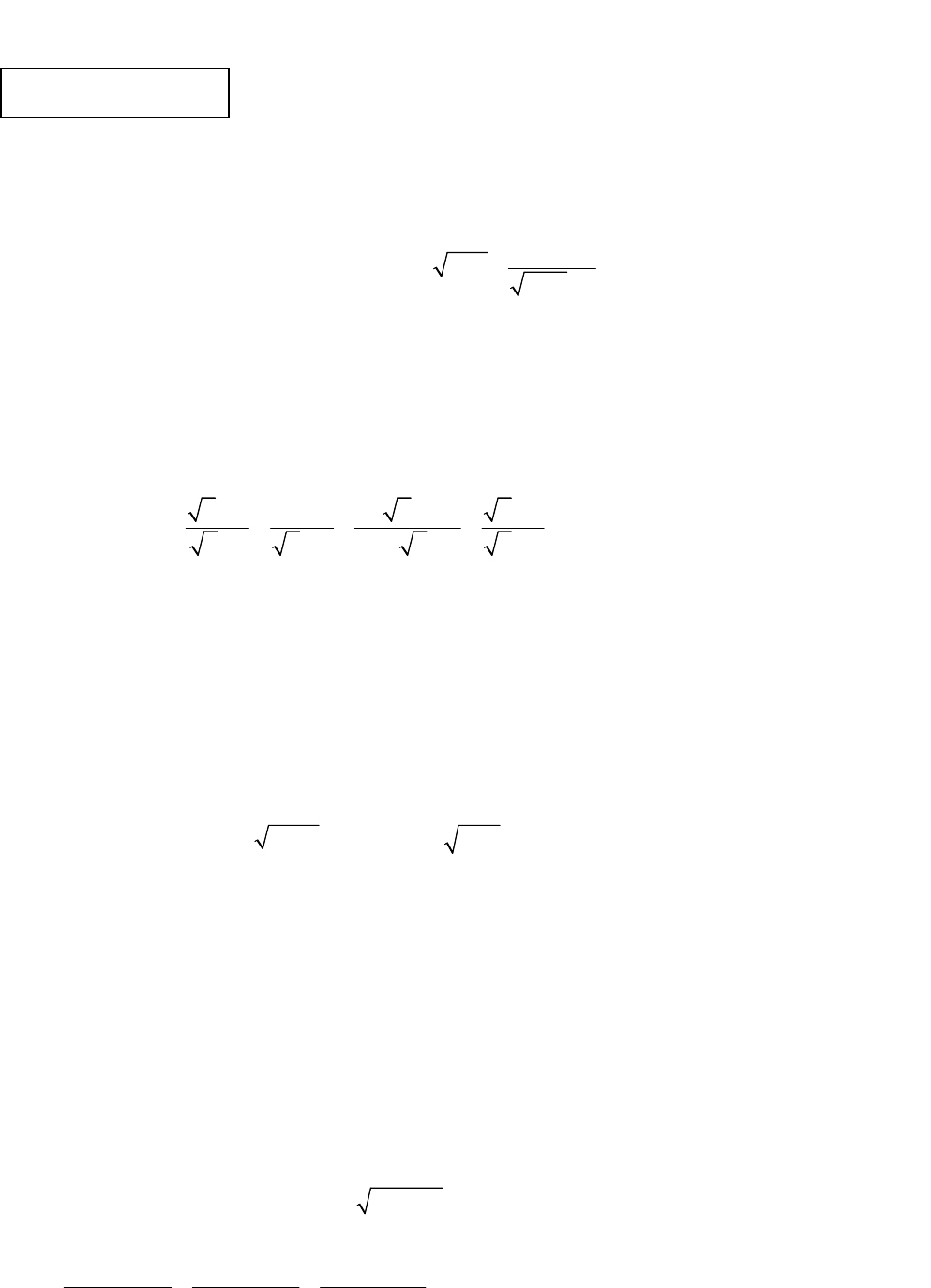
UBND THÀNH PHỐ NAM ĐỊNH

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO

ĐỀ THI TUYỂN SINH LỚP 10 THPT CHUYÊN

NĂM HỌC 2024 - 2025

Môn thi: Toán (chung) – Đề 1

Dành cho học sinh thi vào các lớp chuyên tự nhiên

Thời gian làm bài 120 phút

(Đề thi gồm 01 trang)

Bài 1. (2,0 điểm)

1. Tìm điều kiện xác định của biểu thức

1

3 1

A x

x

  

 

.

2. Tìm tất cả các giá trị của tham số

m

đề đường thẳng

2 1

y x m

   

cắt đường thẳng

2 3

y x

 

tại điểm nằm trên trục hoành.

3. Cho tam giác

ABC

nội tiếp





;3

O cm

. Biết



0 0

70 ; 50 ;

B C 

Tính độ dài cung

BC

nhỏ.

4. Một chiếc bình thuỷ tinh hình trụ có chiều cao

30

cm

và đường kính đáy

20

cm

đựng

đầy nước. Tính số lít nước đựng trong bình (coi rằng thành bình và đáy bình mỏng).

Bài 2. (1,5 điểm)

Cho biểu thức

2 1 3 6 5

.

1 4 5 4 3

x x x

P

x x x x x

 

  

  

 

    

 

với

0

x



.

a) Rút gọn biểu thức

P

.

b) Tìm giá trị lớn nhất của biểu thức

P

.

Bài 3. (1,5 điểm)

1) Cho phương trình

2

2 1 0

x x m

   

(m là tham số).

a) Giải phương trình với

1.

m



b) Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt

1 2

,

x x

thoả mãn

2

1 2 2

2

x x x

  .

2) Giải hệ phương trình













 

2 1 4 1 4

3 1 4 2 1 1 3 .

x y x y y x

x x y y

       





     





Bài 4. (3,0 điểm)

Cho nửa đường tròn





;

O R

, đường kính

BC

,

A

là điểm bất kì trên nửa đường tròn sao

cho

;

AB AC



A

khác

C

. Kẻ

AH

vuông góc với

BC

tại

H

. Gọi

,

M N

lần lượt là hình chiếu

vuông góc của

H

trên

,

AB AC

.

a) Chứng minh

. .

AB AM AC AN



và tứ giác

BCNM

là tứ giác nội tiếp.

b) Đường thẳng

MN

cắt nửa đường tròn





;

O R

tại các điểm

,

E F

(

E

thuộc cung

AB

nhỏ), cắt đoạn thẳng

AO

tại

D

. Chứng minh

OA MN



và

AEH



cân.

c) Đường thẳng

MN

cắt đường thẳng

BC

tại

I

,

IA

cắt nửa đường tròn





;

O R

tại điểm

thứ hai là

K

(

K

khác

A

),

KN

cắt

BC

tại

Q

. Chứng minh

2

.

QH QC QI

 .

Bài 5. (1,0 điểm)

1) Giải phương trình

 

2 2

2 2 1 12 3 16 3

x x x x

    

.

2) Cho

, ,

x y z

là các số dương thoả mãn

1

xyz



. Tìm giá trị lớn nhất của biểu thức

2 2 2 2 2 2

1 1 1

2 3 2 3 2 3

P

x y y z z x

  

     

-------HẾT-------

H

ọ v

à tên thí sinh:………………………

…….

Giám th

ị 1:…………………………………….

SBD:…………………………………………….

Giám th

ị 2: …………………………………….

ĐỀ THI THỬ

UBND THÀNH PHỐ NAM ĐỊNH

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO

ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM

ĐỀ THI THỬ TUYỂN SINH LỚP 10 THPT CHUYÊN

Môn thi: Toán (chung) – Đề 1

Dành cho học sinh thi vào các lớp chuyên tự nhiên

(Hư

ớng dẫn chấm gồm 0

5

trang)

Bài 1: (2,0 điểm)

Câu Nội dung Điểm

1)

0,5 điểm

ĐKXĐ của biểu thức là

1

3

3 1 0

x













  



0, 25

Tìm được

1 3; 2

x x

  

.

0,25

2)

0,5 điểm

Toạ độ giao điểm của đường thẳng

2 3

y x

 

với trục hoành là

3

;0

2



 

 

 

0,25

Vì

2 2

 

, hai đường thẳng cắt nhau tại điểm nằm trên trục hoành



đường thẳng

2 1

y x m

   

đi qua điểm

3

;0

2



 

 

 

3

0 2. 1 2

2

m m



       

.

0,25

3)

0,5 điểm

Tính đư

ợc



0

120

BOC 

0,25

Tính được độ dài cung

BC

nhỏ bằng

 

120

. .3 2

180

cm

 



0,25

4)

0,5 điểm

Thể tích của nước đựng trong bình là

2 3

.10 .30 3000

cm

 



0,25

Số lít nước có trong bình là

3 9,42





(lít)

0,25

Bài 2 (1,5 điểm)

Câu Nội dung Điểm

2)

1,0 điểm

Với

0

x



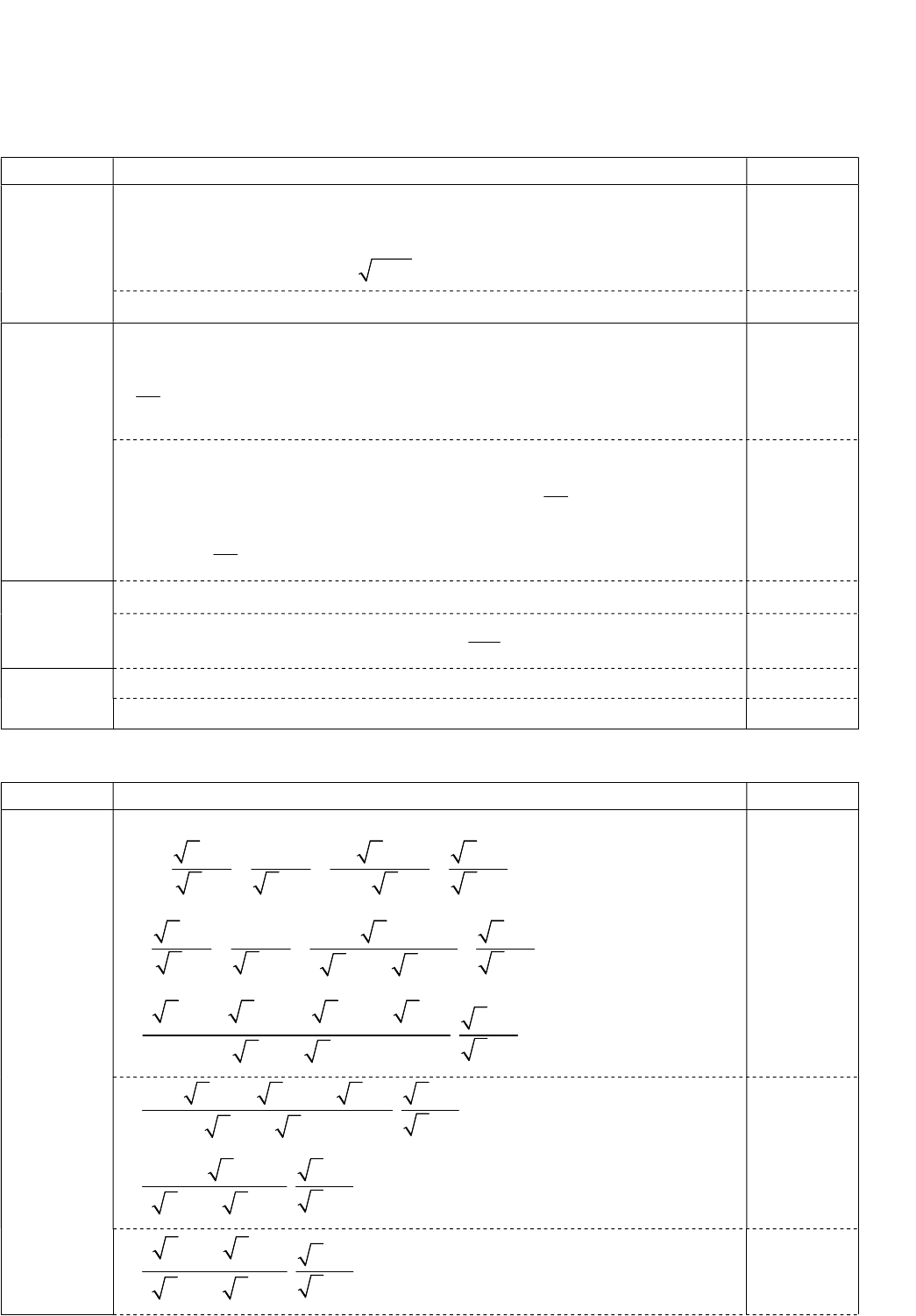
, ta có

  

2 1 3 6 5

.

1 4 5 4 3

2 1 3 6 5

.

1 4 3

1 4

2 4 1 3 6

5

.

3

1 4

x x x

P

x x x x x

x x x

x x

x x x x

x

x x

 

  

  

 

    

 

 

  

 

  

 

  

 

 

     







 

0,25

  

6 8 1 3 6 5

.

3

1 4

4 3 5

.

3

1 4

x x x x x

x

x x

x x x

x

x x

      





 

  





 

0,25









  

1 3

5

.

3

1 4

x x

x

x x

 







 

0,25

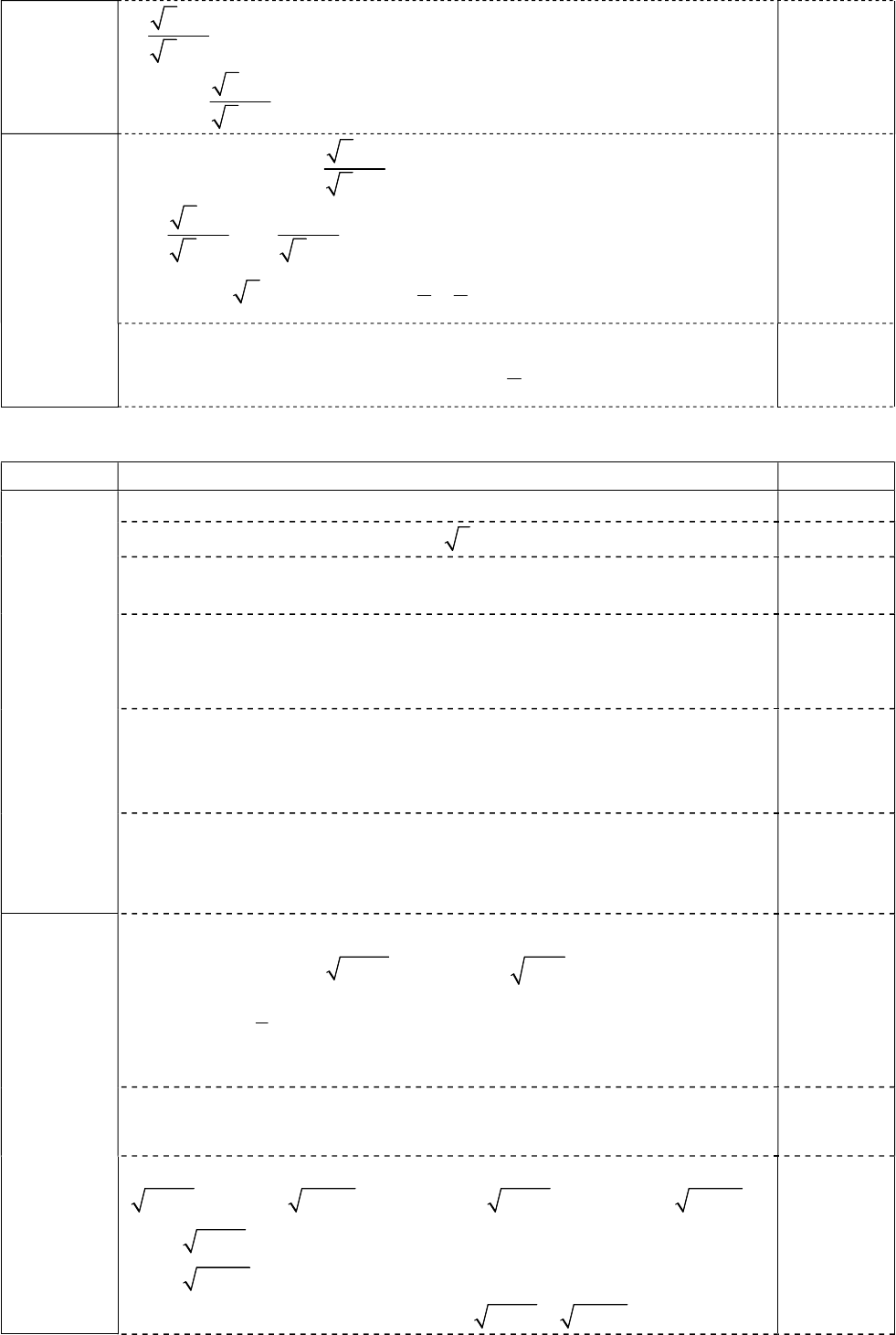
5

4

x







Vậy

5

4

x

P

x







với

0

x



0,25

1b)

0,5 điểm

Theo câu a) ta có

5

4

x

P

x







với

0

x



5 1

1

4 4

x

P

x x



  

 

Vì

1 5

0 4 4 1

4 4

x x P

       

0,25

Dấu

" "



xảy ra khi

0

x



(thoả mãn điều kiện)

Vậy giá trị lớn nhất của biểu thức

P

bằng

5

4

khi

0

x



0,25

Bài 3: (2,5 điểm)

Câu Nội dung Điểm

1)

1,5 điểm

1

a) V

ới

1

m



, phương tr

ình tr

ở th

ành

2

2 2 0

x x

  

0,25

Giải phương trình ta được

1 3

x  

.

0,25

1b)

2

2 1 0

x x m

   

Phương trình có hai nghiệm phân biệt

' 0 2 0 2

m m

        

0,25

Áp dụng định lý Viét ta có





 

1 2

2 1

1 2

x x

x x m

 





  





0,25

Từ

1 2 1 2

2 2

x x x x

    

. Thay vào biểu thức

2

1 2 2

2

x x x

  ta được

2

2 2 2

2 2

x x x

  

Từ đó tìm được

2 2

1; 2

x x

  

0,25

+) Với

2 1

1 3

x x

   

. Thay vào (2) tìm được

2

m



(t/m)

+) Với

2 1

2 0

x x

  

. Thay vào (2) tìm được

1

m

 

(t/m)

Kết luận: Tất cả các giá trị của tham số

m

cần tìm là

2; 1

m m

  

.

0,25

2)

1,0 điểm

Giải hệ phương trình

















   

2 1 4 1 4 1

3 1 4 2 1 1 3 2

x y x y y x

x x y y

       





     





ĐKXĐ:

1

3

1

x

y















0,25

Biến đổi phương trình (1) ta được









1 2 4 0

x y x y

    

Kết hợp ĐKXĐ suy ra

2 4 0

x y

  

0,25

Thay vào phương trình (2) ta có









3 1 2 8 2 3 2 3 1 3 1 2 2 3 2 3

x x x x x x x

            

Đặt

 

3 1

, 0

2 3

x a

a b

x b



 







 





ta được phương trình

2 2

a a b b

  

Giải phương trình tìm được

3 1 2 3

a b x x

    

0,25

Đề thi thử vào 10 chuyên môn Toán (chung) năm 2024 - 2025 phòng GD&ĐT TP Nam Định

VnDoc.com xin gửi tới các bạn Đề thi thử Toán (chung) vào 10 chuyên năm 2024 - 2025 phòng GD&ĐT TP Nam Định để bạn đọc cùng tham khảo. Đây là tài liệu hay cho các bạn ôn luyện, chuẩn bị cho kì thi tuyển sinh vào lớp 10 sắp tới. Đề thi có đáp án đi kèm cho các bạn so sánh đối chiếu sau khi làm xong. Mời các bạn cùng tham khảo chi tiết và tải về bài viết dưới đây.