Đề thi tuyển sinh vào lớp 10 môn Toán (Chuyên) năm học 2015-2016 trường THPT Chuyên Sư Phạm, Hà Nội
Đề thi tuyển sinh vào lớp 10 môn Toán
Đề thi tuyển sinh vào lớp 10 môn Toán (Chuyên) năm học 2015-2016 trường THPT Chuyên Sư Phạm, Hà Nội là đề thi vào lớp 10 chuyên Toán - Tin diễn ra chiều ngày 03.06.2015. VnDoc.com xin giới thiệu tới các bạn tham khảo, nhằm giúp các bạn ôn thi vào lớp 10 hiệu quả nhất.
Đề thi tuyển sinh vào lớp 10 môn Toán (Chung) năm học 2015-2016 trường THPT Chuyên Sư Phạm, Hà Nội
ĐỀ THI TUYỂN SINH
VÀO TRƯỜNG TRUNG HỌC PHỔ THÔNG CHUYÊN NĂM 2015
Môn thi: Toán
(Dùng cho học sinh thi vào chuyên Toán và chuyên Tin)
Thời gian: 120 phút
Câu 1: (2,5 điểm)
1. Cho a ≥ 0, a # 1. Rút gọn biểu thức
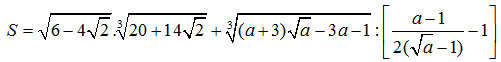
2. Cho x, y thỏa mãn 0< x <1, 0 < y <1 và x/(1 - x) + y/(1 - y) = 1
Tính giá trị của biểu thức
![]()
Câu 2: (2 điểm)
Một xe tải có chiều rộng 2,4m và chiều cao 2,5m muốn đi qua một cái cổng có hình parabol. Biết khoảng cách giữa hai chân cổng là 4m và khoảng cách từ đỉnh cổng (đỉnh parabol) tới mỗi chân cổng là m (bỏ qua độ dầy của cổng)
- Trong mặt phẳng tọa độ Oxy gọi parabol (P) với a < 0 là hình biểu diễn cổng mà xe tải muốn đi qua. Chứng minh a = -1
- Hỏi xe tải có thể qua cổng được không? Tại sao?
Câu 3: (1,5 điểm)
Cho 2 số nguyên a,b thỏa mãn a2 + b2 + 1 = 2(ab + a +b)
Chứng minh a và b là hai số chính phương liên tiếp.
Câu 4: (3 điểm)
Cho tam giác nhọn ABC (AB<AC). M là trung điểm của cạnh BC. O là tâm của đường tròn ngoại tiếp tam giác. Các đường cao AD, BE, CF của tam giác ABC đồng quy tại H. Các tiếp tuyến với (O) tại B,C cắt nhau tại S. Gọi X,Y lần lượt là giao điểm của đường thẳng EF với các đường thẳng BS, AO. Chứng minh rằng:
- MX ┴ BF
- Hai tam giác SMX và DHF đồng dạng
- EF/FY = BC/CD
Câu 5: (1 điểm)
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có các đỉnh là các điểm nguyên (một điểm được gọi là điểm nguyên nếu hoành độ và tung độ của điểm đó là các số nguyên).
Chứng minh rằng hai lần diện tích của tam giác ABC là một số nguyên.
Đáp án đề thi tuyển sinh vào lớp 10 môn Toán
Câu 1: (2,5 điểm)
1.
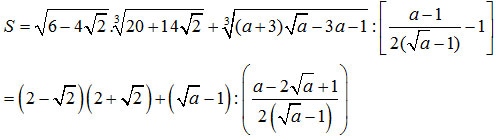
= 2 + 2 =4
2. Ta có: x/(1 - x) + y/1 -y) = 1 ↔ 2(x + y) = 1 3xy
↔ x + y = (1 + 3xy)/2
Thay x + y = (1 + 3xy)/2 ta có:
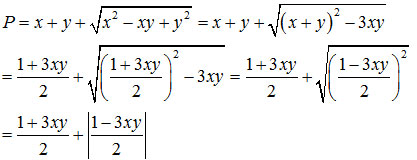
Nếu xy> 1/3 Thì P = 2
Nếu xy < 1/3n thì P = 3xy
Câu 2: (2 điểm)
1. Áp dụng định lý py ta go ta có /y/ = 4 thay x = 2
4 = /a/4 suy ra a= -1 ta được y = - x2
2. Thay x= 1.2 ta có y = 1.44
Khoảng cách còn lại 4 - 1.44 = 2.56 vậy ô tô đi qua được





