Đề khảo sát chất lượng Toán 9 năm 2025 phòng GD&ĐT Hoài Đức, Hà Nội
Đề KSCL môn Toán lớp 9
Lớp:
Lớp 9
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại:
Tài liệu Lẻ
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
UBND HUYỆN HOÀI ĐỨC
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG
MÔN TOÁN 9
Năm học 2025-2026
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
Bài I (1,5 điểm).
Một văn phòng ghi lại số lượt khách hàng trong các ngày làm việc của tháng 8 như
sau:
12
10
13
13
11
15
10
14
15
12
10
15
13
12
10
13
11
11
14
12
11
12
13
15
14
10
1) Lập bảng tần số cho dữ liệu trên.
2) Vẽ biểu đồ tần số dạng đoạn thẳng mô tả dữ liệu trên.
Bài II (1,5 điểm). Cho hai biểu thức A =
và B =
+
với x ≥ 0, x ≠ 1.
1. Tính giá trị của biểu thức A khi x = 4.
2. Rút gọn biểu thức P = B – A.
3. Tìm giá trị nhỏ nhất của biểu thức P.
Bài III (3,0 điểm).
1. Một công nhân phải may 120 chiếc khẩu trang vải trong một thời gian quy
định. Khi thực hiện, nhờ cải tiến kĩ thuật nên mỗi giờ người đó may thêm được 3
chiếc khẩu trang và hoàn thành kế hoạch sớm hơn 2 giờ. Tính số khẩu trang công
nhân đó phải may trong 1 giờ theo quy định?
2. Một canô đi từ bến A đến bến B rồi trở về A ngay. Hai bến sông cách
nhau 40km và tổng thời gian cả đi và về của ca nô là 3 giờ 20 phút. Tính vận tốc
riêng của ca nô biết vận tốc dòng nước là 5km/h.
3. Cho phương trình (ẩn x): x
2
- 2(m - 2)x + 3 - 2m = 0 (1)
a. Chứng tỏ phương trình (1) luôn có nghiệm với mọi giá trị của m.
b. Tìm m để phương trình (1) có 2 nghiệm x
1
, x
2
thoả mãn |x
1
- x
2
| = 24
Bài IV (3,5 điểm).
1. Một hình trụ có chiều cao bằng đường kính đáy. Thể tích của hình trụ là
54 cm
3
. Tính diện tích toàn phần của hình trụ đó.
2. Cho nửa đường tròn (O; R) đường kính AB và điểm M bất kì thuộc nửa
đường tròn (M ≠ A, B). Kẻ tiếp tuyến Ax và By với nửa đường tròn (O) (A, B là
tiếp điểm). Kẻ tiếp tuyến tại M của nửa (O) cắt Ax, By lần lượt tại D, E. Gọi N là
giao điểm của BM và Ax.
a. Chứng minh: Bốn điểm A, D, M, O cùng thuộc một đường tròn.
b. Chứng minh: AD. BE = R
2
c. Chứng minh: D là trung điểm của NA.
Bài V (0,5 điểm).
Cho các số thực không âm x, y thỏa mãn x
2
+ y
2
+ (x – y)
2
= 8. Tìm giá trị
lớn nhất và nhỏ nhất của biểu thức T = x + y.
======== HẾT =======
Họ và tên học sinh: ......................................... Số báo danh: ........................
ĐÁP ÁN VÀ BIỂU ĐIỂM
Bài
Nội dung
Điểm
I.
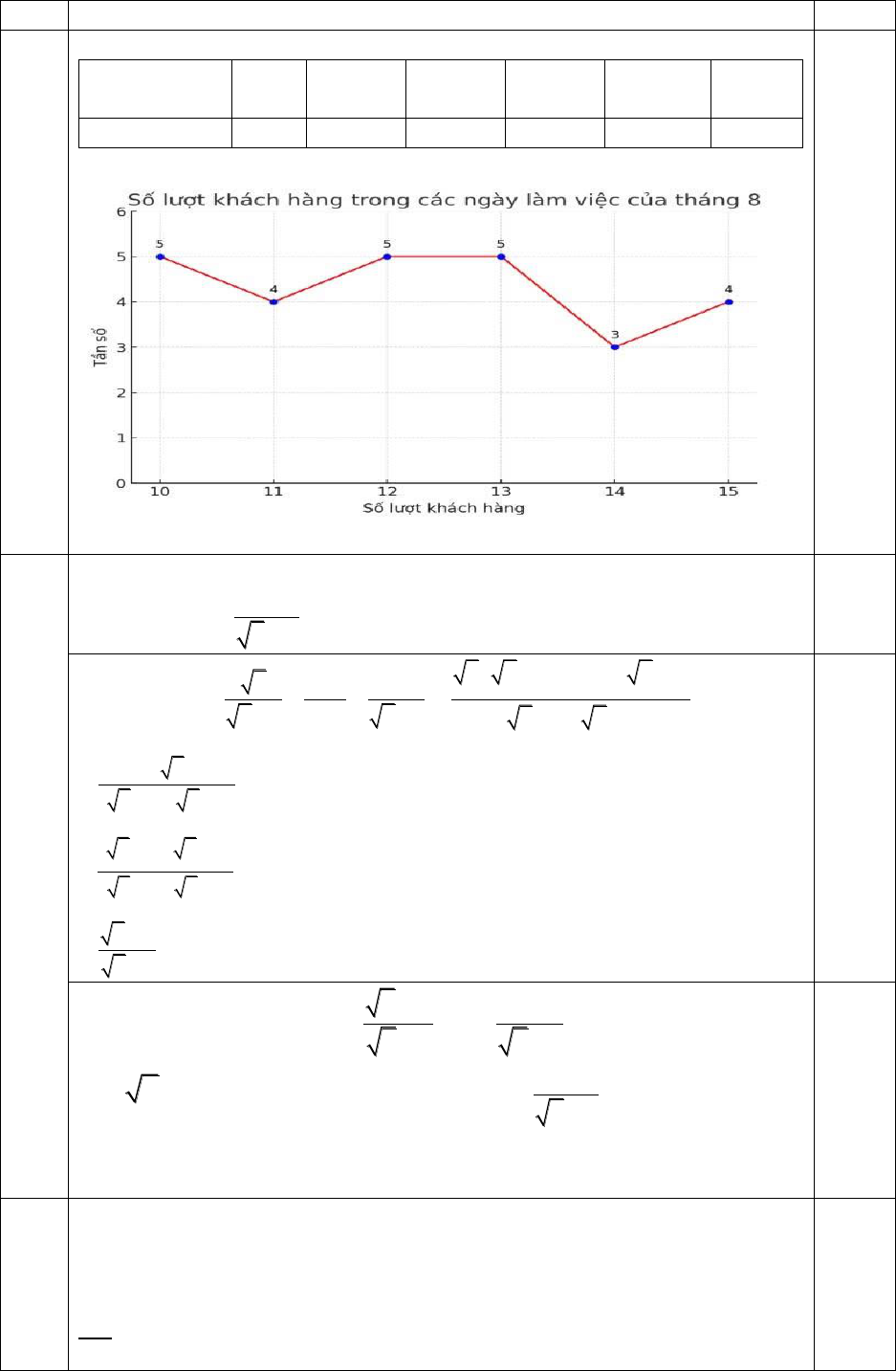
1) Bảng tần số:
Số lượt
khách hàng
10
11
12
13
14
15
Tần số
5
4
5
5
3
4
2) Biểu đồ tần số dạng đoạn thẳng:
0,75
0,75
II.
1. Thay x = 4 (TMĐK) vào biểu thức A
Tính được
3.
3
41
A
0,5
2.
1 6 3 1
63
1
11
11
x x x
x
P B A
x
xx
xx
43
11
xx
xx
13
11
xx
xx
1
3
.
x
x
0,25
0,25
3. ĐK: x ≥ 0, x ≠ 1. Có
4
1.
11
3
xx
x
P
Có:
11x
với mọi x (TMĐK). Suy ra
4
4
1x
. Do đó P ≥-3
Dấu bằng xảy ra khi và chỉ khi x = 0 (TMĐK).
Vậy giá trị nhỏ nhất của biểu thức P = -3 khi x = 0
0,25
0,25
III.
1. Gọi số khẩu trang công nhân đó phải may trong 1 giờ theo quy định là
x (chiếc, x N*)
Thực tế mỗi giờ công nhân đó may được: x + 3 (chiếc)
Thời gian mà công nhân đó may 120 chiếc khẩu trang theo quy định là:
(giờ)
0,25
0,25

Thời gian thực tế công nhân đó may 120 chiếc khẩu trang là:
(giờ)
Lập luận ra PT:
suy ra x
2
+ 3x - 180 = 0
Giải PT ta tìm được x = 12 (tmđk) và x = -15 (ktmđk)
KL: Số khẩu trang công nhân đó phải may trong 1 giờ theo quy định là
12 chiếc.
0,25
0,25
2. Gọi vận tốc riêng của ca nô là x (km/h). Đk: x > 5.
Vận tốc ca nô khi đi xuôi dòng là x + 5 (km/h)
Thời gian ca nô khi đi xuôi dòng là
(h)
Vận tốc ca nô khi đi ngược dòng là x - 5 (km/h)
Thời gian ca nô khi đi ngược dòng là
(h)
Đổi 3 giờ 20 phút =
(giờ).
Ta có phương trình
+
=
Giải phương trình ta được x = 25 (TMĐK) hoặc x = -1 (loại)
Vậy vận tốc riêng của ca nô là 25km/h.
0,25
0,25
0,25
0,25
3. Phương trình: x
2
- 2(m - 2)x + 3 - 2m = 0 (1)
a. ’ = [-(m - 2)]
2
-1.(3 - 2m) = m
2
- 4m + 4 - 3 + 2m
= m
2
- 2m + 1 = (m - 1)
2
≥ 0 với mọi m
Vậy phương trình (1) luôn có nghiệm với mọi m
b. Do phương trình đã cho luôn có nghiệm x
1
, x
2
nên theo định lí Viète
Theo đề bài: |x
1
- x
2
| = 24
(x
1
- x
2
)
2
= 24
2
(x
1
+ x
2
)
2
- 4x
1
x
2
= 24
2
(2m - 4)
2
- 4(3 - 2m) = 24
2
4m
2
- 16m + 16 - 12 + 8m = 24
2
4m
2
- 8m + 4 = 24
2
(2m - 2)
2
= 24
2
Trường hợp 1:
(2m - 2) = 24 Suy ra m = 13
Trường hợp 2:
(2m - 2) = - 24 Suy ra m = - 11
Vậy
13; 11m
thì pt (1) có hai nghiệm x
1
, x
2
thoả mãn |x
1
- x
2
| = 24
0,25
0,25
0,25
0,25
IV
1. Gọi bán kính đáy và chiều cao của hình trụ lần lượt là r và h. Thể tích
của hình trụ là V = r
2
h = 54 (1)
Vì chiều cao của hình trụ bằng đường kính đáy nên h = 2r (2)
Từ (1) và (2) suy ra 2r
3
= 54 hay r
3
= 27 do đó r = 3 (cm)
Từ đó h = 2.3 = 6 (cm)
Diện tích toàn phần của hình trụ là S
tp
= 2.3.6 + 2.3
2
= 54 (cm
2
)
0,25
0,25
Đề khảo sát môn Toán lớp 9
VnDoc giới thiệu đến quý thầy, cô giáo và các em học sinh Đề khảo sát chất lượng Toán 9 năm 2025 phòng GD&ĐT Hoài Đức, Hà Nội. Đề thi gồm cả trắc nghiệm và tự luận, thời gian làm bài 120 phút. Mời các bạn tham khảo chi tiết sau đây.
Ngoài tài liệu trên, VnDoc còn gửi tới các bạn nhiều tài liệu tuyển sinh vào lớp 10 các môn để giúp các em ôn luyện, làm quen với nhiều đề thi khác nhau, chuẩn bị cho kì thi tuyển sinh vào lớp 10 năm học 2025 - 2026.





