Đề khảo sát chất lượng Toán 9 trường THCS Nguyễn Du, Hà Nội năm 2024 - 2025
Đề KSCL môn Toán lớp 9 có đáp án
Lớp:
Lớp 9
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại:
Tài liệu Lẻ
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
Trang 1/2
ĐỀ CHÍNH THỨC
UBND QUẬN HOÀN KIẾM
KHẢO SÁT CHẤT LƯỢNG LỚP 9
TRƯỜNG THCS NGUYỄN DU
Năm học 2024 – 2025
Môn: TOÁN
Thời gian: 120 phút – Đề gồm 02 trang
Bài I. (1,5 điểm)
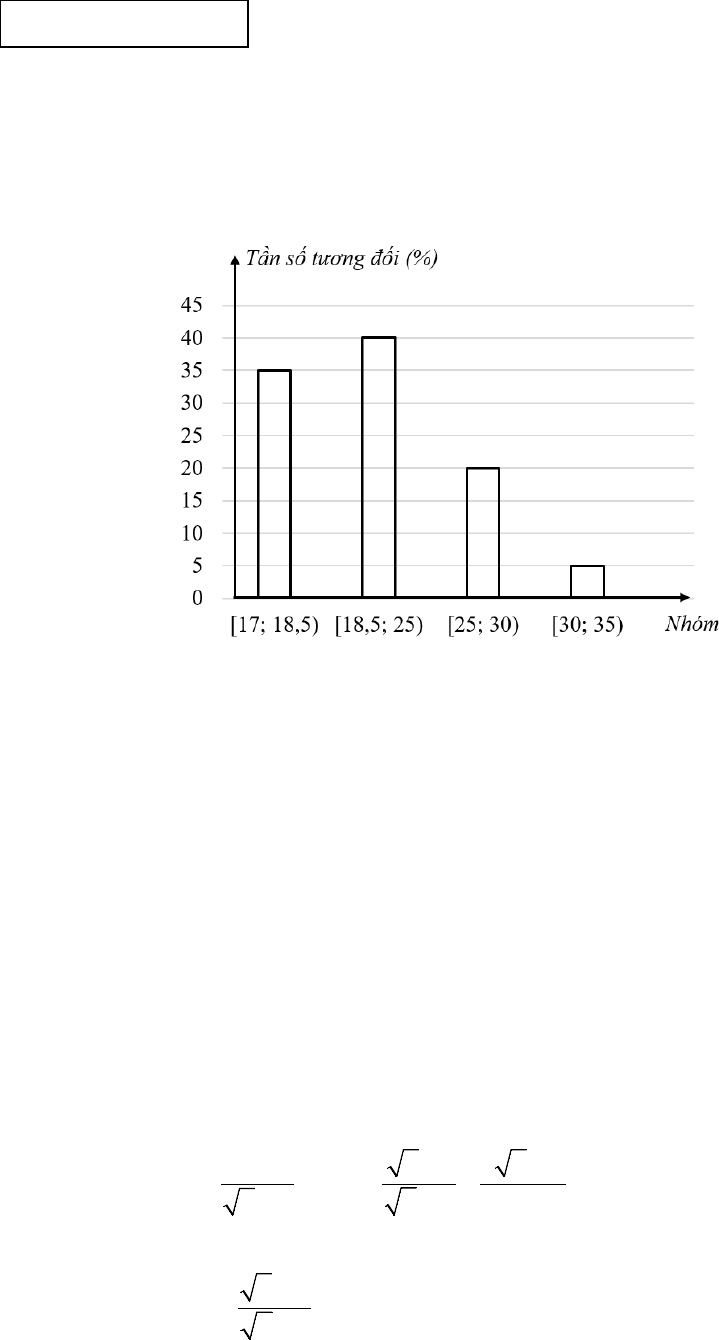
1) Chỉ số khối cơ thể (Body mass index - BMI) được tính nhằm nhận định cơ thể của
một người là gầy hay béo. Biểu đồ tần số tương đối ghép nhóm dưới đây được thống
kê từ chỉ số BMI của 80 người với 4 nhóm: [17; 18,5), [18,5; 25), [25; 30), [30, 35).
a) Tìm tần số tương đối của nhóm [18,5; 25).
b) Cơ thể của người có chỉ số BMI thuộc nhóm [18,5; 25) được nhận định là bình
thường. Tính số người có cơ thể bình thường trong 80 người trên.
2) Chỉ số thông minh (Intelligence Quotient – IQ) của 20 học sinh được cô giáo ghi lại
dưới đây:
90
102
98
116
96
115
86
103
91
100
85
104
102
114
110
102
95
93
99
104
Cô giáo cử ngẫu nhiên một bạn từ những học sinh trên để tham gia một cuộc thi về
trí tuệ. Tính xác suất của biến cố A: “Học sinh được chọn thuộc nhóm thông minh”,
biết nhóm thông minh được quy định là những người có IQ từ 115 đến 130.
Bài II. (1,5 điểm)
Cho hai biểu thức
2
2
A
x
=
−
và
15 6
4
2
xx
B
x
x
++
= +
−
+
với
0, 4.xx≥≠
1) Tính giá trị của biểu thức A khi
1.x =
2) Chứng minh
2
.
2
x
B
x
+
=
−
3) Tìm x để
.AB≥
Trang 2/2
Bài III. (2,5 điểm)
1) Câu lạc bộ bóng đá Juventus đã có một mùa giải bất bại khi không để thua bất kì
trận đấu nào trong tổng cộng 38 trận đấu của mùa giải Serie A 2011-2012 và giành
được tổng cộng 84 điểm. Hỏi câu lạc bộ thắng bao nhiêu trận đấu, hòa bao nhiêu
trận đấu ở mùa giải này? Biết mỗi trận thắng được 3 điểm, mỗi trận hòa được 1 điểm.
2) Năm 2024, bác An góp 300 triệu đồng cùng bác Bình góp vốn đầu tư. Sang năm
2025, bác Bình góp thêm 100 triệu nên tỉ số vốn góp của bác An so với bác Bình
giảm 10%. Hỏi ban đầu bác Bình đã góp bao nhiêu triệu đồng vào năm 2024?
3) Trong mặt phẳng tọa độ Oxy, cho hàm số
2
yx= −
có đồ thị là parabol (P). Tìm tọa
độ điểm
M thuộc (P) sao cho
2 5.OM =
Bài IV. (4,0 điểm)
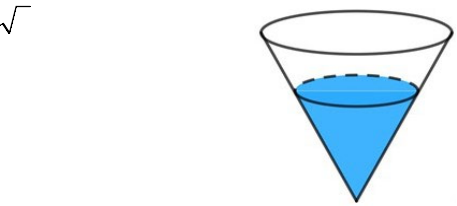
1) Một bể nước trang trí ngoài trời có dạng hình nón với bán
kính đáy 50cm và chiều cao 1,2m.
a) Tính thể tích bể, coi độ dày thành bể là không đáng kể.
b) Người ta đổ 150 lít nước vào bể và đặt vào đó 6 vật trang trí giống nhau có dạng
hình cầu với bán kính 20cm sao cho chúng chìm một nửa vào trong nước. Hỏi
cần đổ thêm bao nhiêu lít nước vào bể để mực nước ngang miệng bể? Biết các
vật trang trí được làm bằng chất liệu không thấm nước. Lấy
3,14.
π
≈
2) Cho tam giác ABC nhọn, không cân, nội tiếp đường tròn (O). Lấy điểm D thuộc
cung nhỏ BC (D khác B, C và AD khác đường kính). Gọi H, K lần lượt là hình chiếu
của D trên AB, BC.
a) Chứng minh bốn điểm B, H, D, K cùng thuộc một đường tròn.
b) I là hình chiếu của D trên AC. Chứng minh
DCI DBH=
và H, K, I thẳng hàng.
c) CE là đường cao của tam giác ACD. Chứng minh EK song song với BH.
Bài V. (0,5 điểm)
Một tập đoàn phát động cuộc thi chạy bộ và bơi lội trực tuyến để nhân viên có thể tham
gia và ghi nhận thành tích mọi lúc mọi nơi. Thể lệ dành cho vận động viên (VĐV) như sau:
• Mục tiêu chính: Hoàn thành tối thiểu 14km chạy bộ và 5km bơi.
• Nếu tham gia trong các ngày thường (từ thứ 2 đến thứ 6), VĐV cần chạy 1km
và bơi 400m.
• Nếu tham gia trong các ngày cuối tuần (thứ 7 và Chủ nhật), VĐV cần chạy 2km
và bơi 1km.
• Số calo tiêu thụ được ở mỗi ngày thường và ngày cuối tuần được BTC quy đổi
lần lượt là 220 calo và 630 calo.
• Cuộc thi diễn ra trong tối đa hai tuần, VĐV hoàn thành mục tiêu chính với
lượng calo tiêu thụ ít nhất đoạt huy chương Vàng.
Em hãy nêu một chiến thuật để VĐV có thể đoạt được huy chương Vàng.
----- HẾT -----

BIỂU ĐIỂM KHẢO SÁT CHẤT LƯỢNG TOÁN 9 NĂM HỌC 2024 – 2025
Bài I
(1,5đ)
1a) Tìm tần số tương đối của nhóm [18,5; 25). 0,5
Đáp số: 40% hoặc 0,4. 0,5
1b) Tính số người có cơ thể bình thường trong 80 người trên. 0,5
Lập đúng phép tính:
80.40%
0,25
Đáp số: 32 người. 0,25
2) Tính xác suất của biến cố A: “HS được chọn thuộc nhóm thông minh” 0,5
Không gian mẫu gồm 20 phần tử.
Có 2 kết quả thuận lợi cho biến cố A, gồm 115, 116.
0,25
Xác suất cần tìm:
2 1
( ) 10%.
20 10
P A
0,25
Bài II
(1,5đ)
1) Tính giá trị của biểu thức A khi
1.
x
0,25
Thay
1
x
(TMĐK) vào A:
2
2.
1 2
A
0,25
2) Chứng minh
2
.
2
x
B
x
0,75
1 2
5 6
2 2 2 2
x x
x
B
x x x x
0,25
2 5 6 4 4
2 2 2 2
x x x x x
B
x x x x
0,25
2
2
2
.
2
2 2
x
x
B
x
x x
0,25
3) Tìm x để
.
A B
0,5
Ta có:
2 2
2 2
x
A B
x x
0 2 0 4
2
x
x x
x
0,25
Kết hợp điều kiện, suy ra
0 4.
x
0,25
Bài III
(2,5đ)
1) Hỏi câu lạc bộ thắng bao nhiêu trận đấu, hòa bao nhiêu trận đấu ở mùa
giải này?
1,0
Gọi số trận thắng và số trận thua lần lượt là x và y (trận;
*
, ).
x y
Mùa giải gồm 38 trận chỉ thắng hoặc hòa nên ta có PT:
38
x y
0,25
Thắng được 3 điểm, hòa được 1 điểm và tổng số điểm là 84 nên ta có PT:
3 84.
x y
0,25
Giải HPT:
38
,
3 84
x y
x y
tìm được
23
x
(TMĐK),
15
y
(TMĐK).
0,25
Kết luận đội thắng 23 trận, hòa 15 trận trong mùa giải. 0,25
Đề khảo sát môn Toán lớp 9 có đáp án
VnDoc giới thiệu đến quý thầy, cô giáo và các em học sinh Đề khảo sát chất lượng Toán 9 trường THCS Nguyễn Du, Hà Nội năm 2024 - 2025. Tài liệu với cấu trúc tự luận, thời gian làm bài 120 phút. Đề thi có đáp án đi kèm, giúp các em so sánh và đối chiếu sau khi làm xong. Sau đây mời các bạn thử sức làm bài.
Ngoài tài liệu trên, VnDoc còn gửi tới các bạn nhiều tài liệu Đề khảo sát lớp 9 và tuyển sinh vào lớp 10 các môn để giúp các em ôn luyện, làm quen với nhiều đề thi khác nhau, chuẩn bị cho kì thi tuyển sinh vào lớp 10 năm học 2025 - 2026.





