Giải bài tập SBT Hình học 11 nâng cao bài 2, 3, 4 chương 3

Giải SBT Hình học 11 bài 2, 3, 4

VnDoc xin giới thiệu tới các bạn học sinh lớp 11 tài liệu Giải bài tập SBT Hình học 11 nâng cao bài 2, 3, 4 chương 3, hy vọng qua bộ tài liệu các bạn học sinh sẽ có kết quả cao hơn trong học tập.

Hai đường thẳng vuông góc. Đường thẳng vuông góc với mặt phẳng. Hai mặt phẳng vuông góc

Câu 16 trang 117 Sách bài tập Hình học 11 Nâng cao

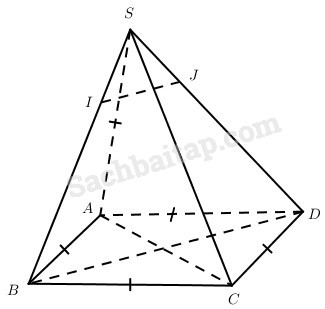
Cho hình chóp S.ABCD có đáy là hình thoi, cạnh bên SA = AB và SA vuông góc với BC.

a) Tính góc giữa hai đường thẳng SD và BC

b) Gọi I, J lần lượt là các điểm thuộc SB và SD sao cho IJ // BD. Chứng minh rằng góc giữa AC và IJ không phụ thuộc vào vị trí của I và J.

Trả lời:

a) Vì BC // AD nên góc giữa SD và BC bằng góc giữa SD và AD.

Từ giả thiết, ta có SA⊥BC nên SA⊥AD mặt khác SA bằng cạnh của hình thoi ABCD, nên ˆSDA=450 là góc phải tìm.

Vậy góc giữa BC và SD bằng 45°.

b) Do ABCD là hình thoi nên AC⊥BD. Mặt khác IJ // BD nên AC⊥IJ tức là góc giữa IJ và AC bằng 90° không đổi.

Câu 17 trang 118 Sách bài tập Hình học 11 Nâng cao

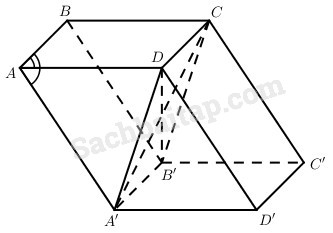
Cho hình hộp ABCD.A’B’C’D’ có các cạnh bằng a, ˆBAD=60⁰,ˆBAA′=ˆDAA′=120⁰.

a) Tính góc giữa các cặp đường thẳng AB với A’D và AC’ với B’D.

b) Tính diện tích các hình A’B’CD và ACC’A’.

c) Tính góc giữa đường thẳng AC’ và các đường thẳng AB, AD, AA’.

Trả lời

Đặt AB^→=x^→,AD^→=y^→,AA′^→=z^→ thì

x^2→=y^2→=z^2→=a²

x^→.y^→=a²/2;

x^→.z^→=−a²/2;

x^→.z^→=−a²/2;

a) Vì AB // A’B’ nên góc giữa AB và A’D bằng góc giữa A’B’ và A’D, đó là góc ˆDA′B′ hoặc 1800−ˆDA′B′ .

Đặt ˆDA′B′=α

Ta có:

A′D=a√3,A′B′=a

DB′^→=x^→−y^→+z^→

⇒DB′^2→=3a²−a²−a²+a²=2a²

Vậy 2a²=a²+3a²−2a.a√3cosα⇒cosα=1/√3

Như thế góc giữa A’D và AB bằng α mà cosα=1/√3

AC′^→=x^→+y^→+z^→

⇒AC′^2→=3a²+a²−a²−a²=2a²

Dễ thấy AB’ = a.

Ta có ADC’B’ là hình bình hành mà AD = AB’, AC’ = B’D nên tứ giác ADC’B’ là hình vuông. Vậy AC’ ⊥ B’D, tức là góc giữa AC’ và B’D bằng 90°.

b)

S_A′B′CD=A′D.A′B′sinˆDA′B′=a√3.a.√6/3

Vậy S_A′B′CD=a²√2

Đặt ˆACC′=β thì AC′²=AC²+CC′²−2AC.CC′.cosβ

hay

2a²=3a²+a²−2a√3.a.cosβ

⇒cosβ=1/√3⇒sinβ=√6/3

Vậy S_ACC′A′=AC.CC′.sinβ=a√3.a.√6/3=a²√2

c) Do zAC′^→=x^→+y^→+z^→

Suy ra:

AC′^→.AB^→=(x^→+y^→+z^→)x^→

=a²+a²/2−a²/2=a²

hay

|AC′^→||AB^→|cos⁡γ=a²

⇒cos⁡γ=1/\(\sqrt{2}\)⇒γ=45⁰

Vậy góc giữa AC’ và AB bằng 45°.

AC′^→.AD^→=(x^→+y^→+z^→)y^→

=a²/2+a²−a²/2=a²

hay

AC′^→|.|AD^→|cos⁡φ=a²⇒cos⁡φ=1/\(\sqrt{2}\)⇒φ=45⁰

Vậy góc giữa AC’ và AD bằng 45°.

AC′^→.AA′^→=(x^→+y^→+z^→)z^→=−a²/2−a²/2+a²=0

Vậy góc giữa AC’ và AA’ bằng 90°.

Câu 18 trang 118 Sách bài tập Hình học 11 Nâng cao

Cho tứ diện ABCD trong đó góc giữa hai đường thẳng AB và CD bằng α. Gọi M là điểm bất kì thuộc cạnh AC, đặt AM = x (0< x < AC). Xét mặt phẳng (P) đi qua điểm M và song song với AB, CD.

a) Xác định vị trí điểm M để diện tích thiết diện của hình tứ diện ABCD khi cắt bởi mp(P) đạt giá trị lớn nhất.

b) Chứng minh rằng chu vi thiết diện nêu trên không phụ thuộc vào x khi và chỉ khi AB = CD.

Trả lời

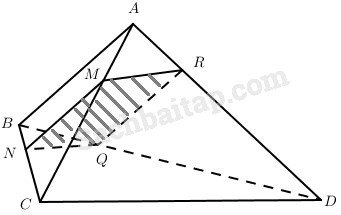
a) Dễ thấy thiết diện là hình bình hành MNPQ và S_MNPQ=NM.NQ.sinˆMNQ .

Do MN // AB, NQ // CD nên góc giữa MN và NQ bằng góc giữa AB và CD do đó sinˆMNQ=sinα.

Ta có:

MN/AB=AC−x/AC⇒MN=AB/AC(AC−x)

NQ=MR,MR/CD=AM/AC=x/AC

⇒MR=CD/AC.x

Vậy S_MNQR=AB.CD/AC²(AC−x)xsinα

Từ đó diện tích thiết diện MNQR đạt giá trị lớn nhất khi và chỉ khi x=AC/2

Như vậy, khi M là trung điểm của AC thì diện tích thiết diện của tứ diện ABCD cắt bởi (P) đạt giá trị lớn nhất.

b) Gọi P là nửa chu vi của thiết diện, khi đó:

p=MN+MR=AB/AC(AC−x)+CD/AC.x

=CD−AB/AC.x+AB

Từ đó, chu vi thiết diện không phụ thuộc vào x khi và chỉ khi:

CD–AB=0 hay AB=CD.

Câu 19 trang 118 Sách bài tập Hình học 11 Nâng cao

Cho hình chóp S.ABCD có đáy là hình bình hành, mặt bên SAB là tam giác vuông tại A. Với điểm M bất kì thuộc cạnh AD (M khác A và D), xét mặt phẳng (α) đi qua điểm M và song song với SA, CD.

a) Thiết diệm của hình chóp S.ABCD khi cắt bởi mp(α) là hình gì?

b) Tính diện tích thiết diện theo a và b; biết AB = a, SA = b, M là trung điểm của AD.

Trả lời

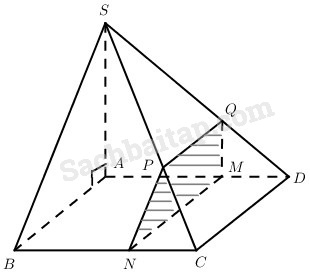
a) Dễ thấy thiết diện là tứ giác MNPQ trong đó MN // QP // CD, MQ // SA.

Do SA ⊥ AB, AB //MN, MQ // SA nên thiết diện MNPQ là hình thang vuông tại M.

b) S_MNPQ=1/2(MN+PQ).MQ

Do M là trung điểm của AD nên:

MQ=1/2SA=1/2b

PQ=1/2CD=1/2a

Vậy S_MNPQ=1/2(a+a/2).b/2=3ab/8

Câu 20 trang 118 Sách bài tập Hình học 11 Nâng cao

Cho tứ diện ABCD. Lấy các điểm M và N lần lượt thuộc các đường thẳng BC và AD sao cho MB^→=kMC^→ và NA^→=kND^→ với k là số thực khác 0 cho trước. Đặt α là góc giữa hai vectơ NMN^→ và BA^→; β là góc giữa hai vectơ MN^→ và CD^→. Tìm mối liên hệ giữa AB và CD để α=β=45⁰

Trả lời

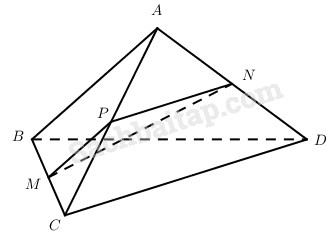
Kẻ MP // AB thì dễ thấy NP // CD. Từ đó, góc giữa MN^→ và BA^→ bằng góc giữa ­MN^→ và MP^→, đó là góc PMN^. Góc giữa MN^→ và CD^→ bằng góc giữa MN^→ và PN^→, đó là góc PNM^.

Vậy hai góc trên bằng nhau và bằng 45° khi và chỉ khi:

MP = NP và ˆMPN=90⁰

Từ đó, suy ra CP/CA.AB=AP/AC.CD và AB⊥CD

hay AB/CD=AP/CP và AB⊥CD

Mặt khác, ta có PA^→=kPC^→⇒AP/PC=|k| .

Vậy giữa AB và CD có mối liên hệ

AB/CD=|k| và AB⊥CD

thì góc giữa hai vectơ MN^→ và BA^→ bằng góc giữa hai vectơ MN^→ và CD^→, cùng bằng 45°).

Câu 21 trang 118 Sách bài tập Hình học 11 Nâng cao

Cho tứ diện ABCD. Gọi I, J, H, K lần lượt là trung điểm của BC, AC, AD, BD. Hãy tính góc giữa hai đường thẳng AB và CD trong các trường hợp sau:

a) Tứ giác IJHK là hình thoi có đường chéo IH=√3IJ

b) Tứ giác IJHK là hình chữ nhật

Trả lời

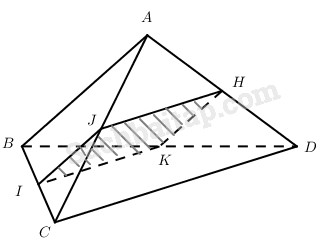
Góc giữa hai đường thẳng AB và CD bằng góc giữa hai đường thẳng IJ và IK, đó là góc ˆJIK hoặc 1800−ˆJIK

a) Vì hình tứ giác IJHK là hình thoi mà IH=√3IJ, nên từ IK²+IH²=4IJ²

ta có: IK²=IJ²

hay IK = IJ

Như vậy JIK là tam giác đều, do đó ˆJIK=60⁰

Vậy góc giữa AB và CD trong trường hợp này bằng 60°.

b) Khi tứ giác IJHK là hình chữ nhật thì ˆJIK=90⁰. Do đó, góc giữa AB và CD bằng 90°.

Câu 22 trang 118 Sách bài tập Hình học 11 Nâng cao

Cho hai tam giác cân ABC và DBC có chung cạnh đáy BC và nằm trong hai mặt phẳng khác nhau.

a) Chứng minh rằng AD vuông góc với CB.

b) Gọi M, N là các điểm lần lượt thuộc các đường thẳng AB và DB sao cho MA^→=kMB^→,ND^→=kNB^→. Tính góc giữa hai đường thẳng MN và BC.

Trả lời:

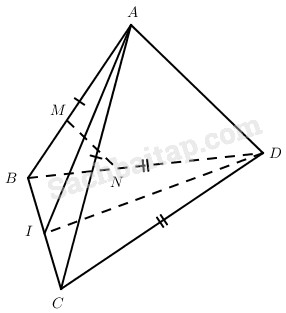
a) Gọi I là trung điểm của BC thì AI⊥BC,DI⊥BC

Ta có AD^→=AI^→+ID^→.

Xét

BC^→.AD^→=BC^→(AI^→+ID^→)

=BC^→.AI^→+BC^→.ID^→=0

Vậy BC⊥AD

b) Từ giả thiết

MA^→=kMB

ND^→=kNB^→

ta có MN // AD

Vậy góc giữa hai đường thẳng MN và BC bằng góc giữa hai đường thẳng AD và BC. Theo câu a) thì AD vuông góc BC, nên góc giữa MN và BC bằng 90°.

Câu 23 trang 118 Sách bài tập Hình học 11 Nâng cao

Cho tứ diện ABCD có CD=4/3AB. Gọi I, J, K lần lượt là trung điểm của BC, AC, BD. Cho biết JK=5/6AB, tính góc giữa đường thẳng CD với các đường thẳng IJ và AB.

Trả lời:

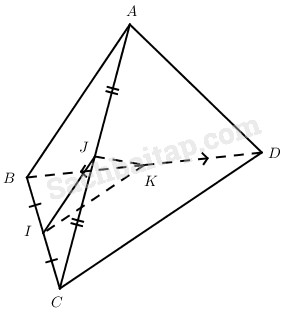
Ta có:

IJ=1/2AB

IK=1/2CD=2/3AB

IJ²+IK²=1/4AB²+4/9AB²=25/36AB²

IJ=12ABIK=12CD=23ABIJ2+IK2=14AB2+49AB2=2536AB2

mà IK²=25/36AB²

nên IJ²+IK²=JK²

Vậy JI⊥IK

Do IJ // AB, IK // CD nên góc giữa AB và CD bằng 90°

Mặt khác IJ // AB mà AB ⊥ CD nên IJ ⊥ CD

Vậy góc giữa IJ và CD bằng 90°.

Câu 24 trang 118 Sách bài tập Hình học 11 Nâng cao

Cho tứ diện ABCD có BC = AD = a, AC = BD = b, AB = CD = c. Đặt α là góc giữa BC và AD; β là góc giữa AC và BD; γ là góc giữa AB và CD. Chứng minh rằng trong ba số hạng a²cosα,b²cosβ,c²cosγ có một số hạng bằng tổng hai số hạng còn lại.

Trả lời:

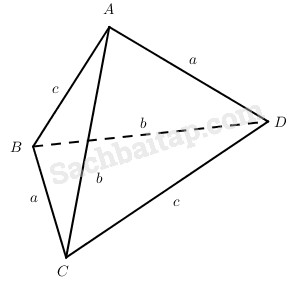
Ta có:

cos⁡(BC^→,DA^→)=2c²−2b²/2a²=c²−b²/a².

Vậy nếu góc giữa BC và AD bằng α thì:

cosα=∣c²−b²∣/a² hay a²cosα=∣c²−b²∣

Tương tự như trên, nếu gọi β là góc giữa AC và BD thì:

b²cos⁡β=|a²−c²|

và γ là góc giữa AB và CD thì

c²cos⁡γ=|b²−a²|.

Với a, b, c lần lượt là dộ dài của BC, CA, AB, không giảm tính tổng quát có thể coi a ≥ b ≥ c. Khi đó:

a²cosα=b²−c²

b²cosβ=a²−c²

c²cosγ=a²−b²

Từ đó, trong trường hợp này ta có b²cosβ=a²cosα+c²cosγ

Câu 25 trang 119Sách bài tập Hình học 11 Nâng cao

Cho tứ diện ABCD có tất cả các cạnh bằng nhau. Gọi M và N lần lượt là trung điểm của AB và CD. Lấy các điểm I, J, K lần lượt thuộc các đường thẳng BC, AC, AD sao cho IB^→=kIC^→,JA^→=kJC^→,KA^→=kKD^→ trong đó k là số khác 0 cho trước. Chứng minh rằng:

a) MN ⊥ IJ và MN ⊥IK

b) AB ⊥ CD

Trả lời

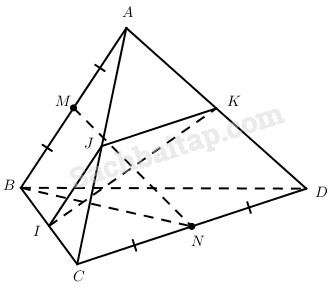
a) Từ

IB^→=kIC^→JA^→=kJC^→

ta có IJ // AB.

Tương tự, ta có IK // CD.

Do các cạnh của tứ diện ABCD bằng nhau và N là trung điểm của CD nên NA = NB.

Mặt khác MA = MB do đó MN ⊥ AB, suy ra MN ⊥ IJ.

Tương tự như trên, ta có MN ⊥ CD và IK // CD nên MN ⊥ JK.

b) Ta có AB^→=AN^→+NB^→.

Từ giả thiết, ta có:

AN⊥CD tức là AN^→.CD^→=0;

BN⊥CDBN⊥CD tức là BN^→.CD^→=0.

Vậy AB^→.CD^→=(AN^→+NB^→).CD^→=0 tức là AB⊥CD

-----------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải bài tập SBT Hình học 11 nâng cao bài 2, 3, 4 chương 3. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Sinh học lớp 11, Vật lý lớp 11, Hóa học lớp 11, Giải bài tập Toán 11 mà VnDoc tổng hợp và đăng tải.