Giải bài tập SBT Hình học 11 nâng cao bài 1 chương 3

Vectơ trong không gian. Sự đồng phẳng của các vectơ

1 979

Toán 11 - Vectơ trong không gian. Sự đồng phẳng của các vectơ

VnDoc xin giới thiệu tới thầy cô và các bạn học sinh tài liệu Giải bài tập SBT Hình học 11 nâng cao bài 1 chương 3, với bộ câu hỏi bài tập kèm theo đáp án sẽ là nguồn thông tin hay để giúp các bạn học sinh có kết quả cao hơn trong học tập.

Giải SBT Toán 11 bài 3: Đường thẳng và mặt phẳng song song

Giải SBT Toán 11 bài 4: Hai mặt phẳng song song

Giải SBT Toán 11 bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian

Giải SBT Toán 11 ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song

Giải bài tập SBT Hình học 11 nâng cao bài 1

Câu 1 trang 113 Sách bài tập Hình học 11 Nâng cao

Cho tứ diện ABCD, M và N là các điểm lần lượt thuộc AB và CD sao cho MA^→=−2MB^→,ND^→=−2NC^→. Các điểm I, J, K lần lượt thuộc AD, MN, BC sao cho IA^→=kID^→,JM^→=kJN^→,KB^→=kKC^→. Chứng minh rằng các điểm I, J, K thẳng hàng.

Trả lời:

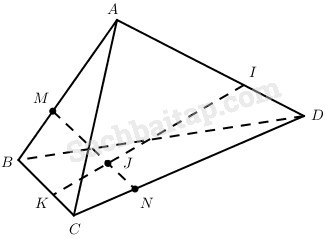
Vectơ trong không gian. Sự đồng phẳng của các vectơ

Cách 1.

Ta có:

IJ^→= IA^→+ AM^→+MJ^→(1)

IJ^→=ID^→+DN^→+NJ^→(2)

Từ (1), (3) ta có:

(1−k)IJ^→=−AM^→−kDN^→

hayIJ^→=1/1−k.AM^→−k/1−kDN^→

Chứng minh tương tự như trên, ta có:

JK^→=1/1−kMB^→−k/1−kNC^→

Mặt khác MA^→=−2MB^→,ND^→=−2NC^→

nên IJ^→=2/1−kMB^→−2k/1−k.NC^→

Từ đó, ta có IJ^→=2IK^→

Vậy ba điểm I, J, K thẳng hàng.

Cách 2.

Vì MA^→=−2MB^→

nên với điểm O bất kì thì OM^→=OA^→+2OB^→/3

Tương tự

ON^→=OD^→+2OC^→/3OI^→=OA^→−kOD^→/1−k;

OK^→=OB^→−kOC^→/1−k;OJ^→=OM^→−kON^→/1−k.

Từ đó, ta có:

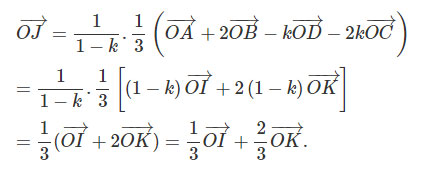
Vectơ trong không gian. Sự đồng phẳng của các vectơ

Mặt khác 1/3+2/3=1

Vậy 3 điểm I, J, K thẳng hàng.

Câu 2 trang 114 Sách bài tập Hình học 11 Nâng cao

Cho hình hộp ABCD.A’B’C’D’; các điểm M, N lần lượt thuộc các đường thẳng CA và DC’ sao cho MC^→−mMA^→,ND^→=mNC′^→. Xác định m để các đường thẳng MN và BD’ song song với nhau. Khi ấy, tính MN biết ˆABC=ˆABB′=ˆCBB′=60⁰ và BA = a, BB’ = b, BC = c.

Trả lời:

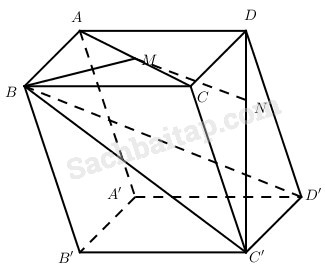
Vectơ trong không gian. Sự đồng phẳng của các vectơ

Xác định m:

Đặt BA^→=a^→,BB^→=b^→,BC^→=c^→ thì BD′^→=a^→+b^→+c^→.

Do MC^→=mMAM^→ nên BM^→=BC^→−mBA1^→/−m=c^→−ma^→/1−m

Tương tự, ta có:

BN^→=BD^→−mBC′^→/1−m=a^→+c^→−m(b^→+c^→)/1−m

=1/1−m.a^→−m/1−m.b^→+c^→.

Từ đó

MN^→=BN^→−BM

=1+m/1−ma^→−m/1−mb^→−m/1−mc^→.

Do AC, BD’ chéo nhau và DC’, BD’ chéo nhau nên

MN//BD′⇔MN^→=kBD′^→⇔

MN^→=ka^→+kb^→+kc^→

Mặt khác a^→,b^→,c^→ không đồng phẳng nên điều ấy xảy ra khi và chỉ khi:

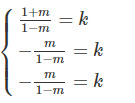
Vectơ trong không gian. Sự đồng phẳng của các vectơ

⇒1+m=−m⇔m=−1/2

Từ đó, ta có k=1/3

Vậy m=−1/2 thì MN // BD’.

Tính MN:

Khi ấy MN^→=1/3(a^→+b^→+c^→)

do đó

MN^2→

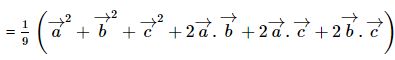
hay MN²=1/9(a²+b²+c²+ab+ac+bc)

tức là MN=1/3 $\sqrt{a^2+b^2+c^2+ab+bc+ca}$

Câu 3 trang 114 Sách bài tập Hình học 11 Nâng cao

Cho hình lăng trụ ABC. A’B’C’. Gọi I và J lần lượt là trung điểm của BB’ và A’C’. Điểm K thuộc B’C’ sao cho KC′^→=−2KB′^→. Chứng minh rằng bốn điểm A, I, J, K cùng thuộc một mặt phẳng.

Trả lời

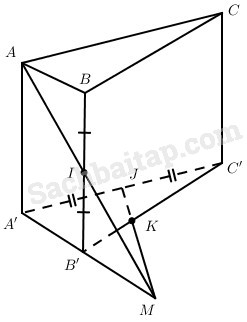
Vectơ trong không gian. Sự đồng phẳng của các vectơ

Đặt AA′^→=a^→,AB^→=b^→,AC^→=c^→

Ta có:

AI^→=1/2(AB^→+AB′^→)

=1/2(b^→+a^→+b^→)

=1/2(a^→+2b^→);(1)

AJ^→=1/2(AA′+−−→AC′)

=1/2(a^→+a^→+c^→)

=1/2(2a^→+c^→).(2)

AK^→=AC′^→+2AB′/3

=a^→+c^→+2(a^→+b^→)/3

=3a^→+2b^→+c^→/3.(3)

Từ (1), (2), (3) ta có AK^→=2/3(AI^→+AJ^→)

Vậy KAI^→,AJ^→,AK^→ đồng phẳng, tức là các điểm A, I, J, K cùng thuộc một mặt phẳng.

Chú ý: Có thể chứng minh các điểm A, I, J, K thuộc một mặt phẳng bằng cách chứng minh AI và JK cắt nhau tại điểm M.

Câu 4 trang 114 Sách bài tập Hình học 11 Nâng cao

Cho hình chóp S.ABCD có đáy là hình bình hành. Một mặt phẳng (P) bất kì không đi qua S, cắt các cạnh bên SA, SB, SC, SD lần lượt tại các điểm A1,B1,C1,D1. Dùng phương pháp vectơ, chứng minh rằng

SA/SA₁+SC/SC₁=SB/SB₁+SD/SD₁

Trả lời:

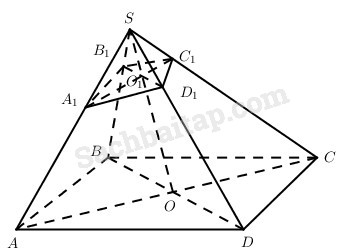
Vectơ trong không gian. Sự đồng phẳng của các vectơ

Vì ABCD là hình bình hành nên

SA^→+SC^→=SB^→+SD^→

hay SD^→=SA^→+SC^→−SB^→

Đặt

SA^→=aSA₁^→,SB^→=bSB₁^→

SC^→=cSC₁^→,SD^→=dSD₁^→

(với a, b, c, d là các số lớn hơn 1)

Khi đó:

SA/SA₁+SC/SC₁=a+c

SB/SB₁+SD/SD₁=b+d

và

SD₁^→=1/d.SD^→=1/d(SA^→+SC^→−SB^→)

=1/d(aSA₁^→+cSC₁^→−bSB₁^→)

=a/d.SA₁^→+c/d.SC₁−b/d.→SB₁^→

Mặt khác các điểm A₁,B₁,C₁,D₁ thuộc mặt phẳng, nên từ đẳng thức đó suy ra

a/d+c/d−b/d=1

tức là a + c = b + d

Như vậy SA/SA₁+SC/SC₁=SB/SB₁+SD/SD₁

Câu 5 trang 114 Sách bài tập Hình học 11 Nâng cao

Cho hình hộp ABCD.A’B’C’D’ có các cạnh bằng m, các góc tại A bằng 60⁰ (ˆBAD=ˆA′AB=ˆA′AD=60⁰)(BAD^=A′AB^=A′AD^=600) . Gọi P và Q là các điểm xác định bởi AP^→=D′A^→,C′Q^→=DC'^→. Chứng minh rằng đường thẳng PQ đi qua trung điểm của cạnh BB’. Tính độ dài đoạn thẳng PQ.

Trả lời:

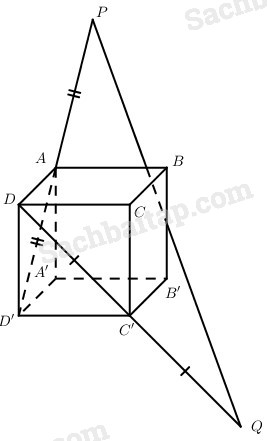
Vectơ trong không gian. Sự đồng phẳng của các vectơ

Đặt AA′^→=a^→,AB^→=b^→,AD^→=c^→

a^→.b^→=b^→.c^→=c^→.a^→=1/2m²

và a^2→=b^2→=c^2→=m² .

Gọi M là trung điểm của BB’ thì

MP^→=MB^→+BA^→+AP^→

Do AP^→=D′A^→=−a^→−c^→.

nên

MP^→=−a^→/2−b^→−a^→−c^→

=−3/2a^→−b^→−c^→

Mặt khác

MQ^→=MB′^→+B′C′^→+C′Q^→

=MB′^→+B′C′^→+DC′^→

=3/2a^→+b^→+c^→

Như vậy MP^→=MQ^→, tức là ba điểm P, M, Q thẳng hàng hay đường thẳng PQ đi qua trung điểm của cạnh BB’.

Ta có:

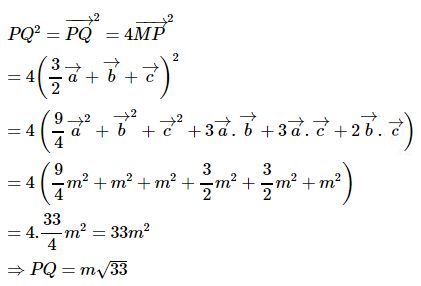
Vectơ trong không gian. Sự đồng phẳng của các vectơ

Câu 6 trang 114 Sách bài tập Hình học 11 Nâng cao

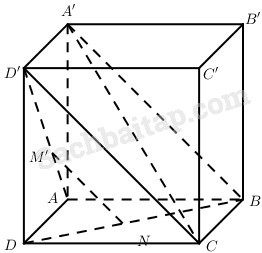
Cho hình hộp ABCD.A’B’C’D’. Gọi D₁,D₂,D₃ lần lượt là điểm đối xứng của điểm D’ qua A, B’, C. Chứng tỏ rằng B là trọng tâm của tứ diện D₁D₂D₃D′.

Trả lời:

Vectơ trong không gian. Sự đồng phẳng của các vectơ

Cách 1.

Đặt AA′^→=a^→,AB^→=b^→,AD^→=c^→

Từ giả thiết, ta có

BD′^→+BD₁^→=2BA^→=−2b^→

mà BD′^→=a^→−b^→+c^→

Vậy BD₁^→=−a^→−b^→−c.^→

Lập luận tương tự như trên, ta có BD₂^→=a^→+b^→−c^→

và BD₃^→=−a^→+b^→+c^→

Vậy BD₁^→+BD₂^→+BD₃^→+BD′^→=0^→

Điều này chứng tỏ B là trọng tâm của tứ diện D₁D₂D₃D′

Cách 2.

Gọi I là giao điểm của BD’ và mp(AB’C) thì D’I = 2IB.

Gọi J là giao điểm của BD’ với mp (D₁D₂D₃), do D₁, D₂, D₃ là các điểm đối xứng của D’ lần lượt qua A, B’, C nên IJ = ID’ hay D′B=3/4D′J.

Mặt khác I là trọng tâm tam giác AB’C nên J là trọng tâm tam giác D₁D₂D₃. Từ đó B là trọng tâm của tứ diện D₁D₂D₃D′.

Câu 7 trang 114 Sách bài tập Hình học 11 Nâng cao

Cho hình lập phương ABCD.A’B’C’D’. Gọi M và N lần lượt là các điểm thuộc AD’ và DB sao cho MA^→=kMD′^→,ND^→=kNB^→(k≠0,k≠1)

a) Chứng minh rằng MN luôn song song với mp (A’BC).

b) Khi đường thẳng MN song song với đường thẳng A’C, chứng tỏ rằng MN vuông góc với AD’ và DB

Trả lời:

Vectơ trong không gian. Sự đồng phẳng của các vectơ

a) Đặt AA′^→=a^→,AB^→=b^→,AD^→=c^→.

Khi đó, ta có:

a^→.b^→=b^→.c^→=c^→.a^→=0.

và a^2→=b^2→=c^2→.

Vì MA^→=kMD′^→ nên MA^→=k(MA^→+AD′^→).

Vậy AM^→=k/k−1(a^→+c^→).

Tương tự như trên, ta có:

AN^→=AD^→−kAB^→/1−k=−k/1−k.b^→+1.1−k.c^→.

Từ đó: MN^→=AN^→−AM^→

=1+k/1−k.c^→+k/1−k(a^→−b^→)

hay ′MN^→=1+k/1−k.BC^→+k/1−k.BA′^→.

Như vậy ba vectơ MN^→,BC^→,BA′^→ đồng phẳng.

Mặt khác AD’, DB cắt mp(A’BCD’); các điểm M, N lần lượt thuộc AD’, DB với k ≠ 0, k ≠ 1 nên MN không thuộc mp(A’BC). Vậy MN song song với mp(A’BC).

b) Ta có A′C^→=−a^→+b^→+c^→; A’C, AD’ chéo nhau; A’C, BD chéo nhau mà M∈AD′,N∈DB. Do đó, đường thẳng MN song song với đường thẳng A’C khi và chỉ khi MN^→=mA′C^→ , tức là

k/1−ka^→−k/1−kb^→+1+k/1−kc^→=−ma^→+mb^→+mc^→

Do a^→,b^→,c^→ là ba vectơ không đồng phẳng nên đẳng thức trên xảy ra khi bà chỉ khi

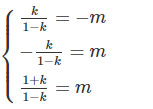
Vectơ trong không gian. Sự đồng phẳng của các vectơ

Suy ra −k=1+k⇔k=−1/2

Vậy khi k=−1/2 thì MN song song với A’C.

Khi đó MN^→=−1/3(a^→−b^→−c^→)

Mặt khác AD′^→=a^→+c^→,DB^→=b^→−c^→

Vậy

MN^→.AD′^→=−1/3(a^2→−c^2→)=0

MN^→.DB^→=−1/3(−b^2→+c^2→)=0

Điều này khẳng định MN vuông góc với AD’ và DB.

Câu 8 trang 114 Sách bài tập Hình học 11 Nâng cao

Cho hình tứ diện ABCD có tất cả các cạnh bằng m. Các điểm M và N lần lượt là trung điểm của AB và CD.

a) Tính độ dài MN.

b) Tính góc giữa đường thẳng MN với các đường thẳng BC, AB và CD.

Trả lời:

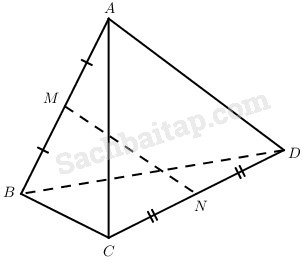
Vectơ trong không gian. Sự đồng phẳng của các vectơ

Đặt AD^→=a^→,AB^→=b^→,AC^→=c^→ .

Khi đó, ta có:

a^→.b^→=b^→.c^→=c^→.a^→=1/2m² và a^2→=b^2→=c^2→=m²

a) Vì M, N là trung điểm của AB và CD nên

MN^→=1/2(AD^→+BC^→)

hay MN^→=1/2(a^→+c^→−b)

Vậy

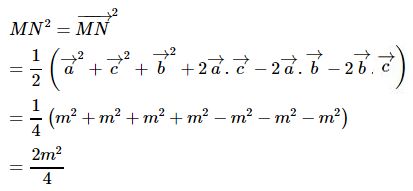
Vectơ trong không gian. Sự đồng phẳng của các vectơ

Tức là MN=m√2/2

b) Ta có

MN^→.AB^→=1/2(a^→+c^→−b^→).b^→

=1/2(a^→.b^→+b^→.c^→−b^→2)=1/2(m²/2+m²/2−m²)=0

Vậy góc giữa hai đường thẳng MN và AB bằng 90°

Ta có:

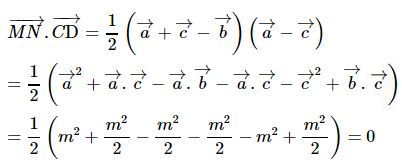
Vectơ trong không gian. Sự đồng phẳng của các vectơ

Vậy góc giữa hai đường thẳng MN và CD bằng 90°.

Ta có:

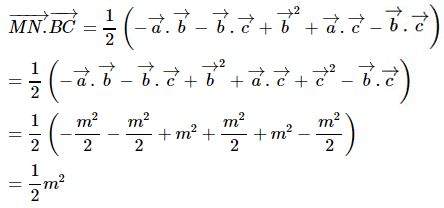
Vectơ trong không gian. Sự đồng phẳng của các vectơ

Tức là:

|MN^→|.|BC^→|cos⁡(MN^→,BC^→)=1/2m²

Từ đó cos(MN^→,BC^→)=m²/2/m.m√2/2=√2/2

Vậy góc giữa hai đường thẳng MN và BC bằng 45°.

Câu 9 trang 114 Sách bài tập Hình học 11 Nâng cao

Cho hình tứ diện ABCD; I và J lần lượt là trung điểm của AB và CD; M là điểm thuộc AC sao cho MA^→=k₁MC^→ ; N là điểm thuộc BD sao cho NB^→=k₂ND^→. Chứng minh rằng các điểm I, J, M, N cùng thuộc một mặt phẳng khi và chỉ khi k₁ = k₂.

Trả lời:

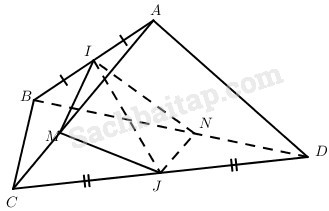
Vectơ trong không gian. Sự đồng phẳng của các vectơ

Vì MA^→=k₁MC^→

nên IM^→=IA^→−k₁IC^→/1−k₁

Tương tự, ta có:

IN^→=IB^→−k₂ID^→/1−k₂=−IA^→−k₂ID^→/1−k₂

Mặt khác: IJ^→=1/2(IC^→+ID^→)

Để các điểm I, I, M, N thuộc một mặt phẳng, điều kiện cần và đủ là ba vectơ IM^→,IN^→,IJ^→ đồng phẳng. Rõ ràng là IN^→ và IJ^→ không cùng phương nên điều khẳng định IM^→,IN^→,IJ^→ đồng phẳng tương đương với IM^→=pIN^→+qIJ^→

hay

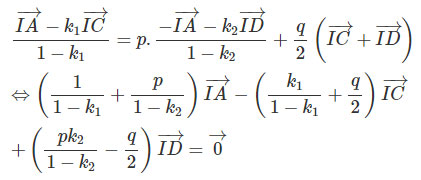
Vectơ trong không gian. Sự đồng phẳng của các vectơ

Do IA^→,IC^→,ID^→ không đồng phẳng nên đẳng thức trên tương đương với

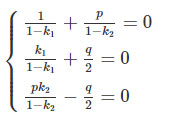
Vectơ trong không gian. Sự đồng phẳng của các vectơ

⇒k₁/1−k₁=−pk₂/1−k₂=k₂/1−k₁

hay k₁ = k₂

Câu 10 trang 115 Sách bài tập Hình học 11 Nâng cao

Cho ba tia Ox, Oy, Oz không đồng phẳng.

a) Đặt ˆxOy=α,ˆyOz=β,ˆzOx=γ. Chứng minh rằng:

cosα+cosβ+cosγ>−3/2

b) Gọi Ox₁,Oy₁,Oz₁ lần lượt là các tia phân giác của các góc xOy, yOz, zOx. Chứng minh rằng nếu Ox₁ và Oy₁ vuông góc với nhau thì Oz₁ vuông góc với cả Ox₁ và Oy₁.

Trả lời:

Lấy E₁,E₂,E₃ lần lượt thuộc các tia Ox, Oy, Oz sao cho OE₁=OE₂=OE₃.

Đặt OE₁^→=e₁^→,OE₂^→=e₂^→,OE₃^→=e₃^→.

a) Do ba tia Ox, Oy, Oz không đồng phẳng nên (e^→₁+e^→₂+e^→₃)²>0, tức là

e²₁^→+e²₂^→+e²₃^→+2(e₁^→.e₂^→+e₂^→.e₃^→+e₃^→.e₁^→)>0

⇔3OE²₁+2OE²₁(cosα+cosβ+cosγ)>0

Vậy cosα+cosβ+cosγ>−3/2

Dễ thấy

OE₁^→+OE₂^→//Ox₁

OE₂^→+OE₃^→//Oy₁^→

OE₃^→+OE₁^→//Oz₁^→

Ox₁⊥Oy₁⇔(OE₁^→+OE₂^→)(OE₂^→+OE₃^→)=0

hay OE²₂^→+OE₁^→.OE₂^→+OE₁^→.OE₃^→+OE₂^→.OE₃^→=0

Ta có:

(OE₁^→+OE₂^→)(OE₃^→+OE₁^→)

=OE₁^2→+OE₁^→.OE₂^→+OE₂^→.OE₃^→+OE₁^→.OE₃^→=0

Vậy Ox₁⊥Oz₁

Tương tự, ta cũng có Oy₁⊥Oz₁

-----------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải bài tập SBT Hình học 11 nâng cao bài 1 chương 3. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Sinh học lớp 11, Vật lý lớp 11, Hóa học lớp 11, Giải bài tập Toán 11 mà VnDoc tổng hợp và đăng tải.

Đánh giá bài viết

1 979