Toán lớp 5 bài 23: Ôn tập chủ đề 1
Với nội dung bài Giải bài tập Toán lớp 5 bài 23: Ôn tập chủ đề 1 chi tiết sách Toán 5 Bình Minh giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 5.
Bài: Ôn tập chủ đề 1
Câu 1. Tính
a) 
\(\frac{9}{8} + \frac{4}{5}\)
b) \(\frac{6}{5} - \frac{5}{{14}}\)
c) \(\frac{2}{9} + \frac{1}{6}\)
d) \(\frac{5}{6} - \frac{3}{4}\)
Phương pháp giải:
Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số đó, rồi cộng (hoặc trừ) hai phân số đã quy đồng.
Lời giải chi tiết:
a) \(\frac{9}{8} + \frac{4}{5} = \frac{{45}}{{40}} + \frac{{32}}{{40}} = \frac{{77}}{{40}}\)
b) \(\frac{6}{5} - \frac{5}{{14}} = \frac{{84}}{{70}} - \frac{{25}}{{70}} = \frac{{59}}{{70}}\)
c) \(\frac{2}{9} + \frac{1}{6} = \frac{4}{{18}} + \frac{3}{{18}} = \frac{7}{{18}}\)
d) \(\frac{5}{6} - \frac{3}{4} = \frac{{10}}{{12}} - \frac{9}{{12}} = \frac{1}{{12}}\)
Câu 2. Chọn giá trị đúng cho mỗi biểu thức
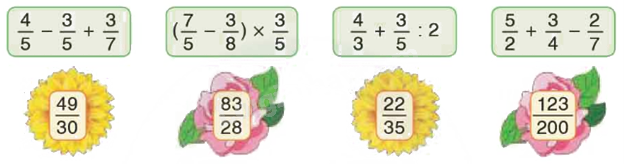
Phương pháp giải:
Thứ tự thực hiện phép tính:
- Khi thực hiện các phép tính trong biểu thức, ta thực hiện từ trái qua phải.
- Nếu biểu thức có dấu ngoặc, ta thực hiện các phép toán trong ngoặc trước.
- Nếu biểu thức gồm các phép tính cộng, trừ, nhân, chia thì ta thực hiện phép toán nhân, chia trước sau đó mới đến phép toán cộng, trừ.
Lời giải chi tiết:
Ta có:
\(\frac{4}{5} - \frac{3}{5} + \frac{3}{7} = \frac{1}{5} + \frac{3}{7} = \frac{7}{{35}} + \frac{{15}}{{35}} = \frac{{22}}{{35}}\)
\(\left( {\frac{7}{5} - \frac{3}{8}} \right) \times \frac{3}{5} = \left( {\frac{{56}}{{40}} - \frac{{15}}{{40}}} \right) \times \frac{3}{5} = \frac{{41}}{{40}} \times \frac{3}{5} = \frac{{123}}{{200}}\)
\(\frac{4}{3} + \frac{3}{5}:2 = \frac{4}{3} + \frac{3}{5} \times \frac{1}{2} = \frac{4}{3} + \frac{3}{{10}} = \frac{{40}}{{30}} + \frac{9}{{30}} = \frac{{49}}{{30}}\)
\(\frac{5}{2} + \frac{3}{4} - \frac{2}{7} = \frac{{70}}{{28}} + \frac{{21}}{{28}} - \frac{8}{{28}} = \frac{{83}}{{28}}\)
Vậy:
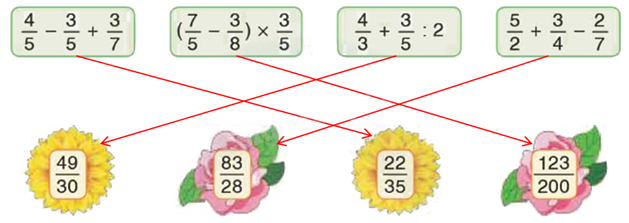
Câu 3
a) Viết mỗi hỗn số sau thành phân số thập phân:
\(63\frac{8}{{10}}\)
\(5\frac{{26}}{{1000}}\)
b) Viết các phân số thập phân sau thành hỗn số:
\(\frac{{276}}{{100}}\)
\(\frac{{7092}}{{1000}}\)
Phương pháp giải:
a) Cách chuyển hỗn số thành phân số:
- Tử số của phân số mới bằng phần nguyên nhân với mẫu số rồi cộng với tử số ở phần phân số.
- Mẫu số bằng mẫu số ở phần phân số.
b) Cách chuyển phân số thập phân thành hỗn số:
- Lấy tử số chia cho mẫu số.
- Thương tìm được là phần nguyên; viết phần nguyên kèm theo một phân số có tử số là số dư, mẫu số là số chia.
Lời giải chi tiết:
a)
\(63\frac{8}{{10}} = \frac{{63 \times 10 + 8}}{{10}} = \frac{{638}}{{10}}\)
\(5\frac{{26}}{{1000}} = \frac{{5 \times 1000 + 26}}{{1000}} = \frac{{5026}}{{1000}}\)
b) Ta có: 276 : 100 = 2 (dư 76)
Vậy:
\(\frac{{276}}{{100}} = 2\frac{{76}}{{100}}\)
Ta có: 7 092 : 1 000 = 7 (dư 92)
\(\frac{{7092}}{{1000}} = 7\frac{{92}}{{1000}}\)
Câu 4. Trong ngày Quốc tế Thiếu nhi, một cửa hàng bán đồ chơi đã bán số búp bê bằng \(\frac{3}{5}\) số siêu nhân và ít hơn số siêu nhân 8 con. Tìm số búp bê và số siêu nhân đã bán.
Phương pháp giải:
- Vẽ sơ đồ.
- Tìm số búp bê và số siêu nhân đã bán theo bài toán tìm hai số khi biết hiệu và tỉ số của hai số đó.
Lời giải chi tiết:
Ta có sơ đồ:
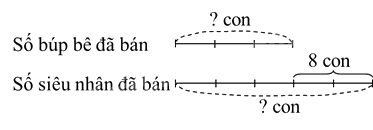
Theo sơ đồ, hiệu số phần bằng nhau là:
5 – 3 = 2 (phần)
Số búp bê đã bán là
8 : 2 x 3 = 12 (con)
Số siêu nhân đã bán là:
12 + 8 = 20 (con)
Đáp số: Búp bê: 12 con ; Siêu nhân: 20 con.
Câu 5. Bác Hai dựng nước trong hai thùng. Lượng nước chứa trong thùng thứ nhất bằng \(\frac{5}{3}\) lượng nước trong thùng thứ hai. Sau khi chia đều lượng nước đó ở cả hai thùng thì mỗi thùng đều chứa 160 l nước. Vậy lúc đầu:
A. Thùng thứ nhất chứa 60 l nước và thùng thứ hai chứa 100 l nước.
B. Thùng thứ nhất chứa 200 l nước và thùng thứ hai chứa 120 l nước.
C. Thùng thứ nhất chứa 120 l nước và thùng thứ hai chứa 200 l nước.
D. Thùng thứ nhất chứa 100 l nước và thùng thứ hai chứa 60 l nước.
Phương pháp giải:
- Tổng số lít nước ở hai thùng lúc đầu = Tổng số lít nước ở hai thùng lúc sau.
- Đưa về bài toán tìm hai số khi biết tổng và tỉ số của hai số đó.
Lời giải chi tiết:
Tóm tắt
Lượng nước trong thùng thứ nhất: \(\frac{5}{3}\) lượng nước trong thùng thứ hai
Sau khi chia đều, mỗi thùng chứa: 160 l nước
Ban đầu thùng thứ nhất: ? l nước
Thùng thứ hai: ? l nước
Bài giải
Vì khi chia đều lượng nước ở cả hai thùng nên tổng số lít nước ở hai thùng lúc đầu bằng tổng số lít nước ở hai thùng lúc sau.
Tổng số lít nước ở hai thùng lúc đầu là:
160 + 160 = 320 (lít)
Ta có sơ đồ:
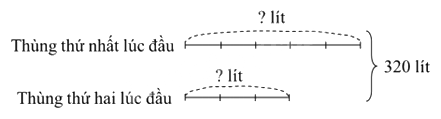
Theo sơ đồ, tổng số phần bằng nhau là:
5 + 3 = 8 (phần)
Lúc đầu thùng thứ nhất chứa số lít nước là:
320 : 8 x 5 = 200 (lít)
Lúc đầu thùng thứ hai chứa số lít nước là:
320 – 200 = 120 (lít)
Đáp số: Thùng thứ nhất: 200 l nước;
Thùng thứ hai: 120 l nước.
Chọn B.
>>>> Bài tiếp theo: Toán lớp 5 bài 24: Số thập phân
