Bất đẳng thức nào sau đây đúng?
Trắc nghiệm Toán 12 Kết nối tri thức bài 3 (Mức độ Dễ)
Trắc nghiệm Toán 12 Kết nối tri thức bài 3: Đường tiệm cận của đồ thị hàm số là bộ đề luyện tập gồm có gồm có 10 câu hỏi trắc nghiệm Toán 12 Kết nối tri thức. Bộ câu hỏi được phân theo các dạng câu hỏi Nhận biết, Thông hiểu, Vận dụng và Vận dụng cao.
Các câu hỏi được để dưới dạng trắc nghiệm trực tuyến cho các bạn trực tiếp làm bài, so sánh đối chiếu và kiểm tra kết quả ngay khi làm xong. Mời các bạn luyện tập.
- Bài kiểm tra này bao gồm 10 câu
- Điểm số bài kiểm tra: 10 điểm
- Xem lại kỹ lý thuyết trước khi làm bài
- Chuẩn bị giấy và bút để nháp trước khi bắt đầu
-
Câu 1:
Thông hiểu
Gọi m, n, p lần lượt là số đường tiệm cận của đồ thị các hàm số sau:
-
Câu 2:
Nhận biết
Tiệm cận đứng của đồ thị hàm số sau là đường thẳng nào?
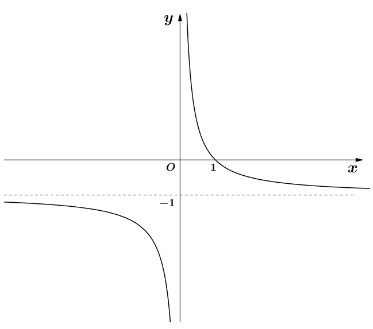
-
Câu 3:
Nhận biết
Cho bảng biến thiên sau:
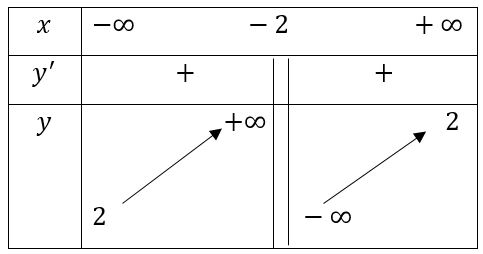
Tiệm cận đứng của hàm số là:
-
Câu 4:
Vận dụng cao
Chọn đáp án đúng:
Đồ thị hàm số
có tâm đối xứng I. Tiếp tuyến d tại điểm M thuộc đồ thị tạo với hai đường tiệm cận của tam giác IAB. Chu vi nhỏ nhất của tam giác IAB là:
-
Câu 5:
Nhận biết
Chọn đáp án đúng:
Cho hàm số
Khẳng định nào sau đây đúng?
-
Câu 6:
Vận dụng
Chọn đáp án đúng:
Tồn tại đúng một điểm M(a,b) trên đường cong
sao cho tiếp tuyến của đường cong tại M tạo với hai trục toạ độ một tam giác có diện tích bằng 2. Tính 4a + b + 10.
-
Câu 7:
Thông hiểu
Chọn đáp án đúng:
Tìm m để đồ thị hàm số
không có tiệm cận đứng.
-
Câu 8:
Thông hiểu
Chọn đáp án đúng:
Cho hàm số
. Nếu đồ thị hàm số có tiệm cận ngang y = 1 và tiệm cận đứng
thì giá trị của a và c là:
-
Câu 9:
Vận dụng
Chọn đáp án đúng:
Đường thẳng y = kx + m vừa là tiếp tuyến của đường cong
, vừa cắt hai trục toạ độ A, B sao cho tam giác OAB cân tại gốc tạo độ O. Tính giá trị của biểu thức S = m + k
-
Câu 10:
Nhận biết
Đồ thị hàm số sau có tiệm cận ngang là đường thẳng nào sau đây?
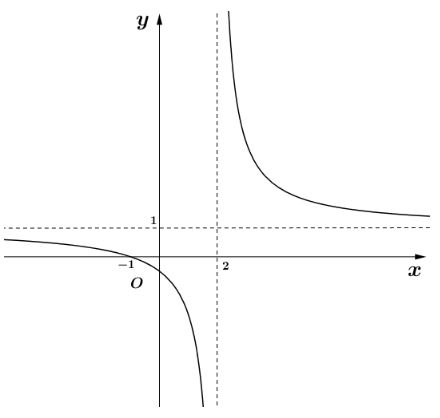
Chúc mừng Bạn đã hoàn thành bài!
-
Nhận biết (40%):
2/3
-
Thông hiểu (30%):
2/3
-
Vận dụng (20%):
2/3
-
Vận dụng cao (10%):
2/3
- Thời gian làm bài: 00:00:00
- Số câu làm đúng: 0
- Số câu làm sai: 0
- Điểm số: 0
- Điểm thưởng: 0

