VnDoc.com

Bài tập ôn tập chương 3 Hình học lớp 8

Câu hỏi ôn tập Hình học 8 chương 3

Bài tập ôn tập chương 3 Hình học Toán lớp 8

I. Nội dung ôn tập chương 3 Hình học 8
II. Bài tập trắc nghiệm ôn tập chương 3 hình học 8
III. Bài tập tự luận ôn tập chương 3 hình học 8

Bài tập ôn tập chương 3 môn Toán lớp 8: Tam giác đồng dạng do VnDoc sưu tầm và tổng hợp giúp các bạn ôn tập và củng cố kiến thức về tam giác đồng dạng, các hệ thức đã được học trong chương 3 Hình học lớp 8. Mời quý thầy cô và các bạn cùng tham khảo.

Đây là Đề cương ôn tập chương 3: Tam giác đồng dạng, bao gồm các phần bài tập theo chuẩn khung chương trình đào tạo của Bộ Giáo Dục ban hành. Qua đó sẽ giúp các bạn học sinh kiểm tra kiến thức cũng như củng cố lại các kiến thức đã được học về chương 3: Tam giác đồng dạng. Đồng thời đây cũng là tài liệu để các bạn học sinh có thể tham khảo và ôn luyện chuẩn bị cho kì thi học kỳ 2 sắp tới.

Bài tập chương 3 Toán lớp 8: Tam giác đồng dạng

I. Nội dung ôn tập chương 3 Hình học 8

+ Công thức tính diện tích hình chữ nhật, hình vuông, tam giác, hình thang, hình bình hành và hình thoi

+ Định lí Ta-lét, định lí Ta-lét đảo và hệ quả của định lí Ta-lét

+ Tính chất đường phân giác trong tam giác

+ Các trường hợp đồng dạng của tam giác thường và tam giác vuông

+ Công thức tính tỉ số đường cao, diện tích của hai tam giác đồng dạng

II. Bài tập trắc nghiệm ôn tập chương 3 hình học 8

Câu 1: Hãy chọn phát biểu đúng

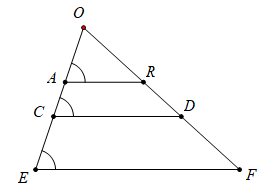
bài tập ôn tập chương 3 hình học 8 ảnh số 1

A. $\frac{{OA}}{{OB}} = \frac{{AB}}{{CD}}$ $\frac{{OA}}{{OB}} = \frac{{AB}}{{CD}}$ C. $\frac{{AB}}{{EF}} = \frac{{OC}}{{OE}}$ $\frac{{AB}}{{EF}} = \frac{{OC}}{{OE}}$

B. $\frac{{OC}}{{OD}} = \frac{{OE}}{{OF}}$ $\frac{{OC}}{{OD}} = \frac{{OE}}{{OF}}$ D. $\frac{{CD}}{{EF}} = \frac{{OD}}{{OF}}$ $\frac{{CD}}{{EF}} = \frac{{OD}}{{OF}}$

Câu 2: Trong các phát biểu sau, phát biểu nào sai

A. Hai tam giác đều thì đồng dạng với nhau

B. Hai tam giác cân thì đồng dạng với nhau

C. Hai tam giác vuông có hai góc nhọn tương ứng bằng nhau thì đồng dạng với nhau

D. Hai tam giác vuông có hai cặp cạnh góc vuông tỉ lệ với nhau thì đồng dạng với nhau.

Câu 3: Cho tam giác ABC đồng dạng với tam giác A'B'C' với tỉ số đồng dạng $k = \frac{1}{3}$ $k = \frac{1}{3}$.Phát biểu nào sau đây là đúng

A. Nếu đường cao $A'H' = 5$ thì đường cao AH là

B. Nếu đường trung tuyến thì đường trung tuyến AM = 2

C. Nếu chu vi $\Delta ABC$ $\Delta ABC$ là 12 thì chu vi $\Delta A$ $\Delta A'B'C'$ là 4

D. Nếu diện tích $\Delta A$ $\Delta A'B'C'$ là 243 thì diện tích $\Delta ABC$ $\Delta ABC$ là 27

E. Nếu đường phân giác $A'D' = 12$ thì đường phân giác AD = 4

Câu 4: Chọn phương án đúng

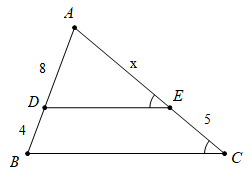
bài tập ôn tập chương 3 hình học lớp 8 ảnh số 2

A. DE // BC C. $\Delta ADE$ $\Delta ADE$ đồng dạng $\Delta ABC$ $\Delta ABC$

B. $\frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}$ $\frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}$ D. $\frac{{AD}}{{AB}} = \frac{{BC}}{{DE}}$ $\frac{{AD}}{{AB}} = \frac{{BC}}{{DE}}$

Câu 5: Giá trị của x là:

A. 9 B. 9,5 C. 10 D. 10,5

Câu 6: Chọn phương án đúng

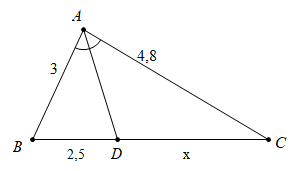
bài tập ôn tập chương 3 hình học 8 ảnh số 2

A. $\frac{{AB}}{{AC}} = \frac{{BD}}{{BC}}$ $\frac{{AB}}{{AC}} = \frac{{BD}}{{BC}}$ C. $\frac{{BD}}{{AB}} = \frac{{AC}}{{DC}}$ $\frac{{BD}}{{AB}} = \frac{{AC}}{{DC}}$

B. $\frac{{BD}}{{AB}} = \frac{{AC}}{{DC}}$ $\frac{{BD}}{{AB}} = \frac{{AC}}{{DC}}$ D. $\frac{{AD}}{{BD}} = \frac{{AC}}{{DC}}$ $\frac{{AD}}{{BD}} = \frac{{AC}}{{DC}}$

Câu 7: Giá trị của x là:

A. 3,5 B. 4 C. 4,8 D. 5,6

Câu 8: Chọn phát biểu đúng trong các phát biểu dưới đây:

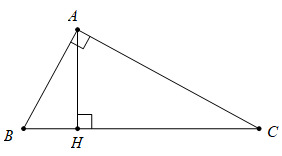
bài tập ôn tập chương 3 hình học 8 ảnh số

A. $\Delta ABC$ $\Delta ABC$đồng dạng $\Delta ACH$ $\Delta ACH$

B. $\Delta ABC$ $\Delta ABC$đồng dạng $\Delta HAC$ $\Delta HAC$

C. $\Delta ABC$ $\Delta ABC$đồng dạng $\Delta AHC$ $\Delta AHC$

D. $\Delta ABC$ $\Delta ABC$đồng dạng $\Delta HCA$ $\Delta HCA$

Câu 9: Chọn phát biểu đúng:

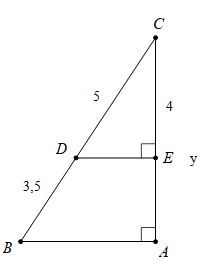
bài tập ôn tập chương 3 hình học 8 ảnh số 5

A. DE // AB C. $\frac{{CD}}{{CB}} = \frac{{CE}}{{CA}}$ $\frac{{CD}}{{CB}} = \frac{{CE}}{{CA}}$

B. $\frac{{CD}}{{CB}} = \frac{{DE}}{{AB}}$ $\frac{{CD}}{{CB}} = \frac{{DE}}{{AB}}$ D. $\Delta CDE = \Delta CBA$ $\Delta CDE = \Delta CBA$

Câu 10: Giá trj của y là:

A. 6 B. 6,8 C. 7 D. 7,2

III. Bài tập tự luận ôn tập chương 3 hình học 8

Bài 1: Cho $\Delta ABC$ $\Delta ABC$cân tại A. Tia phân giác góc B và C cắt AC và AB theo thứ tự ở D và E. Tính độ dài cạnh AB biết DE = 10cm, BC= 16cm.

Bài 2: Cho $\Delta ABC$ $\Delta ABC$. Đường phân giác $\widehat {BAC}$ $\widehat {BAC}$ của cắt cạnh CB tại D. Qua D kẻ đưởng thẳng song song với AB và cắt AC tại E. Tính AE, EC, DE biết BD = 7,5cm; CD = 5cm; AC = 10cm.

Bài 3: Cho $\Delta ABC$ $\Delta ABC$, trực tâm H. Chu vi tam giác ABC bằng 60cm. Gọi M, N, Q lần lượt là ba điểm trên HA, HB, HC sao cho AM = 3MH; BN = 3NH; CQ = 3QH. Tính chu vi

Bài 4: Cho hình chữ nhật ABCD có AB = 8cm, BC = 6cm. Kẻ $AH \bot BD$ $AH \bot BD$ tại H.

a) Chứng minh $\Delta ADH$ $\Delta ADH$ ∽ $\Delta BDA$ $\Delta BDA$từ đó suy ra $A{D^2} = DH.DB$ $A{D^2} = DH.DB$

b) Tính độ dài đoạn thẳng DH, AH

c) Vẽ tia phân giác AM của $\widehat {BAD}$ $\widehat {BAD}$ (M thuộc BD) Tính độ dài đoạn thẳng MB, MD

d) Đường thẳng AH cắt DC tại I và cắt đường thẳng BC tại K. Tính tỉ số diện tích của hai tam giác ABH và tam giác BKH.

e) Chứng minh: $A{H^2} = HI.HK$ $A{H^2} = HI.HK$

Bài 5: Cho hình thang cân ABCD có AB // DC; và đường chéo BD vuông góc với cạnh bên BC. Vẽ đường cao BH, AK.

a) Chứng minh $B{C^2} = HC.DC$ $B{C^2} = HC.DC$

b) Chứng minh $\Delta AKD$ $\Delta AKD$ ∽ $\Delta BHC$ $\Delta BHC$

c) Cho BC = 15cm, DC = 25cm. Tính diện tích hình thang ABCD.

Bài 6: Cho tam giác cân ABC (AB = AC). Vẽ các đường cao BH, CK, AI của tam giác ABC

a) Chứng minh KH // BC

b) Chứng minh HC.AC = IC.BC

c) Cho biết BC = a, AB = AC = b. Tính độ dài đoạn thẳng HK theo a và b.

Bài 7: Cho $\Delta ABC$ $\Delta ABC$ vuông tại A, đường cao AH, biết AC = 6cm, AB = 8cm.

a) Chứng minh $A{B^2} = BH.BC$ $A{B^2} = BH.BC$

b) Trên tia đối của tia AC lấy điểm D tùy ý, dựng AK vuông góc với DB tại K. Chứng minh $\Delta BHK$ $\Delta BHK$ ∽ $\Delta BDC$ $\Delta BDC$

c) Cho biết AD = 15cm. Tính diện tích $\Delta BHK$ $\Delta BHK$

d) Kẻ đường phân giác AM của , từ M kể đường thẳng song song với AC cắt AH tại I. Chứng minh BI là tia phân giác của $\widehat {ABC}$ $\widehat {ABC}$

Bài 8: Cho vuông tại B, đường cao BH, biết AB = 15cm, BC = 20cm.

a) Chứng minh $BH.AC = BA.BC$

b) Từ H kẻ $HM \bot AB, HN \bot BC.$ $HM \bot AB, HN \bot BC.$Chứng minh tam giác BMN và tam giác BCA đồng dạng.

c) Tính diện tích tứ giác AMNC.

d) Gọi O là trung điểm MN. Chứng minh diện tích tam giác COB bằng diện tích tam giác COH

e) Gọi BK là đường cao tam giác BMN. Chứng minh BK đi qua trung điểm đoạn thẳng AC. Chứng minh $\frac{{BM}}{{BA}} + \frac{{BN}}{{BC}} = 1$ $\frac{{BM}}{{BA}} + \frac{{BN}}{{BC}} = 1$

Bài 9: Cho $\Delta MNP$ $\Delta MNP$vuông tại M (MP > MN) Kẻ tia phân giác của góc N cắt PM tại I. Từ P hạ đoạn thẳng PK vuông góc với tia phân giác NI, K thuộc NI

a) Chứng minh tam giác MNI và tam giác KPI đồng dạng

b) Chứng minh $\widehat {INP} = \widehat {KPI}$ $\widehat {INP} = \widehat {KPI}$

c) Cho MN = 3cm, MP = 4cm. Tính IM.

Bài 10: Cho tam giác ABC vuông tại A, đường cao AH, phân giác BD cắt AH tại E

a) Chứng minh tam giác ADE cân

b) Chứng minh AE.BD = BE.DC

c) Từ D kẻ DK vuông góc với BC tại K. Tứ giác ADKE là hình gì?

Bài 11: Cho hình thang vuông ABCD có $\widehat A = \widehat D = {90^o}, BC \bot BD, BC = 2cm, CD = 8cm$ $\widehat A = \widehat D = {90^o}, BC \bot BD, BC = 2cm, CD = 8cm$

a) Chứng minh tam giác ABD đồng dạng với tam giác BDC

b) Tính các góc B và Ccủa hình thang ABCD

c) Tính diện tích của hình thang ABCD

Bài 12: Cho tam giác ABC vuông ở A; AB = 15cm; CA = 20cm, đường cao AH

a) Tính độ dài BC, AH

b) Gọi D là điểm đối xứng với B qua H. Vẽ hình bình hành ADCE. Tứ giác ABCE là hình gì? Chứng minh.

c) Tính độ dài AE

d) Tính diện tích tứ giác ABCE

Bài 13: Cho hình thang cân MNPQ (MN // PQ, MN < PQ), NP = 15cm, đường cao NI = 12cm, QI = 16cm

a) Tính độ dài IP, MN

b) Chứng mỉnh rằng $QN\bot NP$ $QN\bot NP$

c) Tính diện tích hình thang MNPQ

d) Gọi E là trung điểm của PQ. Đường thẳng vuông góc với EN tại N cắt đường thẳng PQ tại K. Chứng minh rằng $K{N^2} = KP.KQ$ $K{N^2} = KP.KQ$

Bài 14: Cho hình bình hành ABCD, trên tia đối của tia DA lấy DM = AB, trên tia đối của tia BA lấy BN = AD. Chứng minh:

a) Tam giác CBN và tam giác CDM cân

b) Tam giác CBN đồng dạng với tam giác MDC

c) Chứng minh M, C, N thẳng hàng

Bài 15: Cho tam giác ABC (AB < AC) hai đường cao BE và CF gặp nhau tại H, các đường thẳng kẻ từ B song song với CF và từ C song song với BE gặp nhau tại D. Chứngminh

a) Tam giác ABE đồng dạng với tam giác ACF

b) AE.CB = AB.EF

c) Gọi I là trung điểm của BC. Chứng minh H, I, D thẳng hàng

Bài 16: Gọi AC là đường chéo lớn của hình bình hành ABCD. E và F lần lượt là hình chiếu của C trên AB và AD, H là hình chiếu của D trên AC. Chứng minh rằng

a) AD.AF = AC.AH

b) $AD.AF + AB.AE = A{C^2}$ $AD.AF + AB.AE = A{C^2}$

Bài 17: Cho có các góc đều nhọn. Các đường cao AD, BE, CF cắt nhau ở H

a) Chứng minh rằng AE.AC = AF.AB

b) Chứng minh rằng tam giác AFE đồng dạng với tam giác ACB

c) Chứng minh rằng tam giác FHE đồng dạng với tam giác BHC

Chứng minh rằng $BF.BA + CE.CA = B{C^2}$ $BF.BA + CE.CA = B{C^2}$

---------

Ngoài Đề cương ôn tập chương 3 Hình học, mời các bạn học sinh tham khảo thêm các đề thi học kì 2 Toán 8, đề kiểm tra học kì 2 các môn lớp 8 như Anh, Văn, Địa lý,... mà chúng tôi đã sưu tầm và chọn lọc. Với Đề cương ôn tập chương 3 hình học này sẽ giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tập tốt!