Đề thi học sinh giỏi môn Toán lớp 6 năm học 2014 - 2015 huyện Hoằng Hóa, Thanh Hóa

Đề thi học sinh giỏi môn Toán lớp 6

Đề thi học sinh giỏi môn Toán lớp 6 năm học 2014 - 2015 huyện Hoằng Hóa, Thanh Hóa là tài liệu học tập môn Toán hữu ích dành cho các bạn học sinh lớp 6. Đề thi HSG lớp 6 này có đáp án đi kèm, giúp các bạn ôn tập và tra cứu hiệu quả, sẵn sàng cho kỳ thi học sinh giỏi THCS. Mời các bạn tham khảo.

Bài 1 (4,5 điểm) Tính giá trị các biểu thức sau:

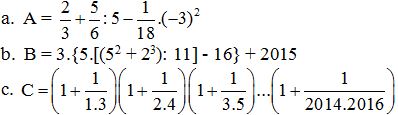
Bài 2 (4,0 điểm)

a. Tìm số tự nhiên x biết 8.6 + 288 : (x - 3)² = 50

b. Tìm các chữ số x; y để chia cho 2; 5 và 9 đều dư 1.

c. Chứng tỏ rằng nếu p là số nguyên tố lớn hơn 3 thì p² - 1 chia hết cho 3.

Bài 3 (4,5 điểm)

a. Cho biểu thức:

Tìm tất cả các giá trị nguyên của n để B là số nguyên.

b.Tìm các số nguyên tố x, y sao cho: x² + 117 = y²

c. Số 2¹⁰⁰ viết trong hệ thập phân có bao nhiêu chữ số .

Bài 4 (5,0 điểm)

Cho góc xBy = 55⁰. Trên các tia Bx; By lần lượt lấy các điểm A; C (A ≠ B; C ≠ B). Trên đoạn thẳng AC lấy điểm D sao cho góc ABD = 30⁰

a. Tính độ dài AC, biết AD = 4cm, CD = 3cm.

b. Tính số đo của góc DBC.

c. Từ B vẽ tia Bz sao cho góc DBz = 90⁰. Tính số đo góc ABz.

Bài 5 (2,0 điểm)

a. Tìm các chữ số a, b, c khác 0 thỏa mãn:

b. Cho . Chứng minh A là số tự nhiên chia hết cho 5.

Đáp án đề thi học sinh giỏi môn Toán lớp 6

Bài 1 (4,5 điểm)

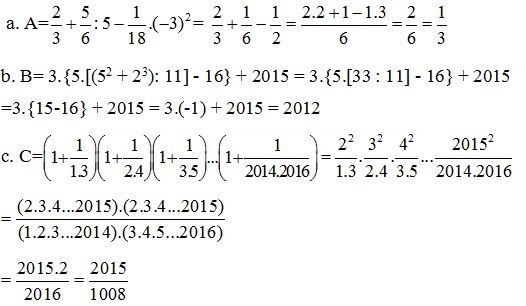
Bài 2 (4,0 điểm)

a. Biến đổi được: (x - 3)² = 144 = 12² = (-12)² ↔ x - 3 = 12 hoặc x - 3 = -12 ↔ x = 15 hoặc x = -9

Vì x là số tự nhiên nên x = -9 (loại). Vậy x = 15

b. Do chia cho 2 và 5 đều dư 1 nên y = 1. Ta có A =

Vì A = chia cho 9 dư 1 → - 1 chia hết cho 9 →

↔ x + 1 + 8 + 3 + 0 chia hết cho 9 ↔ x + 3 chia hết cho 9, mà x là chữ số nên x = 6

Vậy x = 6; y = 1

c. Xét số nguyên tố p khi chia cho 3.Ta có: p = 3k + 1 hoặc p = 3k + 2 (k ∈ N*)

Nếu p = 3k + 1 thì p² - 1 = (3k + 1)² -1 = 9k² + 6k chia hết cho 3

Nếu p = 3k + 2 thì p² - 1 = (3k + 2)² - 1 = 9k² + 12k chia hết cho 3

Vậy p² - 1 chia hết cho 3.

Bài 3 (4,5 điểm)

a. Để B nhận giá trị nguyên thì n - 3 phải là ước của 5

=> n - 3 ∈ {-1; 1; -5; 5} => n ∈ { -2 ; 2; 4; 8}

Đối chiếu đ/k ta được n ∈ {- 2; 2; 4; 8}

b. Với x = 2, ta có: 2² + 117 = y² → y² = 121 → y = 11 (là số nguyên tố)

* Với x > 2, mà x là số nguyên tố nên x lẻ y² = x² + 117 là số chẵn

=> y là số chẵn

kết hợp với y là số nguyên tố nên y = 2 (loại)

Vậy x = 2; y = 11.

c. Ta có: 10³⁰= 1000¹⁰ và 2¹⁰⁰ =1024¹⁰. Suy ra: 10³⁰ < 2¹⁰⁰ (1)

Lại có: 2¹⁰⁰= 2³¹.2⁶³.2⁶ = 2³¹.512⁷.64 và 10³¹=2³¹.5²⁸.5³=2³¹.625⁷.125

Nên: 2¹⁰⁰< 10³¹ (2). Từ (1) và(2) suy ra số 2¹⁰⁰ viết trong hệ thập phân có 31 chữ số.