Đề thi thử vào lớp 10 môn Toán (chuyên Toán - Tin) lần 1 năm học 2015-2016 trường THPT Chuyên Nguyễn Huệ
Đề thi thử vào lớp 10 môn Toán trường THPT chuyên Nguyễn Huệ
Đề thi thử vào lớp 10 môn Toán (chuyên Toán - Tin) lần 1 năm học 2015-2016 trường THPT Chuyên Nguyễn Huệ là đề thi thử vào lớp 10 môn Toán có đáp án mà VnDoc xin được gửi đến các bạn tham khảo, chuẩn bị cho kì thi vào lớp 10 môn Toán được chắc chắn và hiệu quả nhất, nhất là với các bạn ôn thi vào các trường THPT Chuyên.
Tổng hợp đề thi vào lớp 10 được tải nhiều nhất
Tuyển tập đề thi vào lớp 10 môn Ngữ văn các tỉnh năm học 2014 - 2015
|
TRƯỜNG THPT CHUYÊN NGUYỄN HUỆ
|
KỲ THI THỬ VÀO LỚP 10 CHUYÊN THPT LẦN THỨ NHẤT NĂM HỌC 2015 - 2016 Môn thi: TOÁN Thời gian làm bài: 150 phút (dùng cho thí sinh thi vào lớp chuyên Toán và chuyên Tin) |
Bài I (2 điểm)
- Tính tổng sau: 4/3 + 16/15 + 36/35 + ...+ 2500/2499
- Chứng minh rằng nếu p là số nguyên tố lớn hơn 3 thì p² - 1 chia hết cho 24.
Bài II (3 điểm)
- Cho các số thực x, y thỏa mãn: (√((x² + 1) + x) + (√((y² + 4) + y) = 2. Chứng minh rằng 2x + y = 0.
- Giải phương trình: 4√(x² + 3x) + 2√(2x - 1) = 7x + 3.
Bài III (3 điểm)
Cho điểm P tùy ý nằm trong đường tròn tâm O bán kính R. Qua P kẻ hai dây cung tùy ý AC và BD vuông góc với nhau. Gọi M là trung điểm của AB.
- Chứng minh PM vuông góc với CD.
- Chứng minh AC² + BD² = 8R² - 4OP².
- Chứng minh rằng AB² + BC² + CD² + DA² không phụ thuộc vào vị trí điểm P.
Bài IV (1 điểm)
Tìm các số tự nhiên x, y thỏa mãn: x² - 4x = 3y - 3.
Bài V (1điểm)
Những điểm trong mặt phẳng được tô bằng một trong ba màu.Chứng minh rằng luôn tìm được hai điểm cùng màu cách nhau đúng bằng 1.
------------------------- Hết----------------------
(Giám thị không giải thích gì thêm)
Họ và tên thí sinh: .....................................................Số báo danh:...............................
Chữ ký của giám thị số 1:..........................................Chữ ký của giám thị số 2:..................................
Đáp án đề thi thử vào lớp 10 môn Toán
Bài I:
1. Tính tổng
Ta có: 4/3 + 16/15 + 36/35+...+ 2500/2499 = (1 + 1/3) + (1 + 1/15) + (1 + 1/35) +...+ (1 + 1/2499)
= 25 + (1/3 + 1/(3.5) + 1/(3.5) + ... + 1/(49.51))
= 25 + 0,5 × (1 - 1/3 + 1/3 - 1/5 + 1/5 - 1/7 + ....+ 1/49 -1/51).
= 25 + 0,5 × (1 - 1/51) = 1300/51.
2. Chứng minh:
Ta có (p - 1)p(p + 1) chia hết cho 3 mà (p,3 ) = 1 nên (p-1)(p+1) chia hết cho 3 (1).
Vì p là số nguyên tố lớn hơn 3 nên p là số lẻ, p-1 và p+1 là hai số chẵn liên tiếp. Trong hai số chẵn liên tiếp, có một số là bội của 4 nên tích của chúng chia hết cho 8 (2).
Từ (1) và (2) suy ra (p-1)(p+1) chia hết cho hai số nguyên tố cùng nhau 3 và 8.
Vậy (p-1)(p+1) chia hết 24.
Bài II: Giải phương trình:
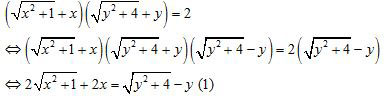
![]()
Lấy (1) trừ (2) theo vế với vế, ta được : 4x = -2y hay 2x + y = 0 (đpcm)


