Số thực là gì? Các dạng Toán về số thực
Số thực và các dạng toán về số thực
Số thực là gì, tính chất của số thực và các dạng toán về số thực.... Đây là những nội dung quan trọng được học trong chương trình Toán 7 học kì 1. Để giúp các em nắm vững phần này, VnDoc gửi tới các em lý thuyết về số thực và các bài tập vận dụng giúp các em ghi nhớ kiến thức được học hiệu quả.
I. Số thực là gì?
− Tập hợp R là ký hiệu của tập hợp số thực, gồm các số thực.
− Số thực gồm số hữu tỉ và số vô tỉ: R = Q ∪ I
− Tập số thực R phủ kín trục số.
− Tập hợp số thực được biểu diễn như sau:
N ⊂ Z ⊂ Q ⊂ R
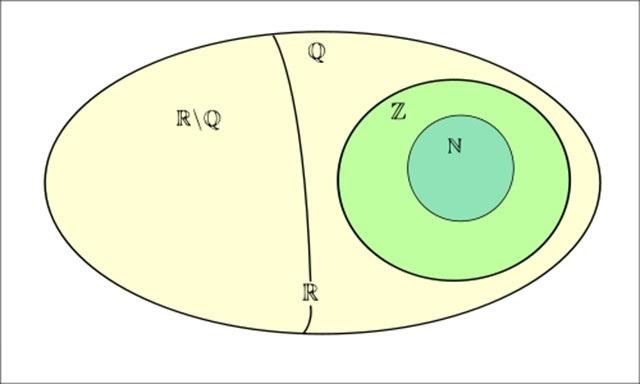
N: Tập hợp số tự nhiên
Z: Tập hợp số nguyên
Q: Tập hợp số hữu tỉ
I = R\Q: Tập hợp số vô tỉ
II. Tính chất số thực
− Trong tập hợp R, ta cũng định nghĩa các phép toán cộng trừ, nhân, chia, lũy thừa, căn bậc…Và trong các phép toán các số thực cũng có các tính chất như các phép toán trong tập hợp các số hữu tỉ.
− Với mọi số thuộc R, ta có:
+ Cộng với số 0: a + 0 = a
+ Tính chất giao hoán: a + b = b + a
+ Tính chất kết hợp: (a + b) + c = a + (b + c)
III. Các dạng bài tập của số thực và cách giải
Dưới đây là một số dạng bài tập về số thực để các bạn tham khảo thêm:
Dạng 1. Bài tập về định nghĩa các tập hợp số
Phương pháp giải: Trước tiên, bạn cần nắm vững các kí hiệu tập hợp số:
Nắm vững quan hệ của các tập hợp số nói trên: N ⊂ Z ⊂ Q ⊂ R ; I ⊂ R. |
Ví dụ 1: Điền dấu ∈, ∉, ⊂ thích hợp vào chỗ trống (…):
3 …. Q ; 3 …. R ; 3… I ; − 2,53… Q ;
0,2(35) …. I ; N …. Z ; I …. R.
Lời giải:
a) 3 ∈ Q ; 3 ∈ R ; 3 ∉ I ; − 2,53 ∈ Q ;
b) 0,2(35) ∉ I ; N ⊂ Z ; I ⊂ R.
Ví dụ 2. Điền vào chỗ trống (…) trong những phát biểu sau:
a) Nếu a là một số thực thì a là số … hoặc số …
b) Nếu b là số vô tỉ thì b sẽ được viết dưới dạng …
Lời giải:
a) Nếu a là một số thực thì a là số hữu tỉ hoặc số vô tỉ.
b) Nếu b là số vô tỉ thì b sẽ được viết dưới dạng số thập phân vô hạn không tuần hoàn.
Ví dụ 3. Trong những nhận định dưới đây, câu nào đúng, câu nào sai:
a) Nếu a là số nguyên thì a cũng là một số thực
b) Chỉ có số 0 không là số hữu tỉ dương và cũng không là số hữu tỉ âm
c) Nếu a là số tự nhiên thì số a không phải là số vô tỉ
Lời giải:
Các câu a) và c) đúng
Câu b) sai vì ngoài số 0 ra thì số vô tỉ cũng không là số hữu tỉ dương và cũng không là số hữu tỉ âm.
Ví dụ 4. Hãy tìm các tập hợp:
a) Q ∩ I ;
b) R ∩ I.
Lời giải:
a) Q ∩ I = Ø
b) Vì I ⊂ R nên R ∩ I = I.
Dạng 2: So sánh các số thực
Phương pháp giải:Cần nắm vững những kiến thức dưới đây:
|
Ví dụ 1: Điền chữ số thích hợp vào (…):
a) – 3,02 < – 3,…1
b) – 7,5…8 > – 7,513 ;
c) – 0,4…854 < – 0,49826 ;
d) – 1,…0765 < – 1,892.
Lời giải:
a) – 3,02 < – 301
b) – 7,508 > – 7,513 ;
c) – 0,49854 < – 0,49826 ;
d) – 1,90765 < – 1,892.
Ví dụ 2. Cho các số thực: – 3,2 ; 1 ; – 1/2 ; – 7,4 ; 0 ; – 1,5. Hãy sắp xếp:
a) Theo thứ tự từ nhỏ đến lớn.
b) Theo thứ tự từ bé đến lớn theo giá trị tuyệt đối của chúng.
Lời giải:
a) Sắp xếp theo thứ tự như sau: – 3,2 < – 1,5 < – 1/2 < 0 < 1 < 7,4.
b) Vì 0 < 1/2 < 1 < 1,5 < 3,2 < 7,4
Vậy: |0| < |– 1/2| < |1| < |– 1,5| < |– 3,2| < |7,4|.
Dạng 3. Tìm số chưa biết ở trong một đẳng thức
Phương pháp giải
|
Ví dụ: Tìm x, biết: 3,2x + (– 1,2x) + 2,7 = – 4,9
Lời giải:
3,2x + (– 1,2x) + 2,7 = – 4,9
[3,2 + (–1,2)] . x + 2,7 = – 4,9
2x = – 4,9 – 2,7
2x = – 7,6
x = – 7,6 : 2
x = – 3,8
Vậy x = – 3,8.
Dạng 4 .Tính giá trị biểu thức
Phương pháp giải
|
\(A=-5,13:\left ( 5\frac{5}{28} -1\frac{8}{9} .1,25+1\frac{16}{63} \right )\)
\(B=\left ( 3\frac{1}{3}.1,9+ 19,5 : 4\frac{1}{3} \right ).\left ( \frac{62}{75}-\frac{4}{25} \right )\)
Lời giải:
\(A=-5,13:\left ( 5\frac{5}{28} -1\frac{8}{9} .1,25+1\frac{16}{63} \right )\)
\(A=-5,13:\left ( \frac{145}{28} -\frac{17}{9} .\frac{5}{4} +\frac{79}{63} \right )\)
\(A=-5,13:\left ( \frac{1305}{252} -\frac{595}{252}+\frac{316}{252} \right )\)
\(A=-\frac{513}{100}:\frac{1026}{252}=-1,26\)
\(B=\left ( 3\frac{1}{3}.1,9+ 19,5 : 4\frac{1}{3} \right ).\left ( \frac{62}{75}-\frac{4}{25} \right )\)
\(B=\left ( \frac{10}{3}.\frac{19}{10} + \frac{39}{2} : \frac{13}{3} \right ).\left ( \frac{62}{75}-\frac{12}{75} \right )\)
\(B=\left (\frac{19}{3} + \frac{9}{2} \right ). \frac{2}{3}\)
\(B= \frac{65}{6} . \frac{2}{3} =\frac{65}{9}\)
.................
Trên đây, VnDoc đã gửi tới các bạn tài liệu Số thực là gì? Các dạng Toán về số thực. Hy vọng đây là tài liệu hữu ích giúp các bạn hiểu rõ hơn về số thực, tính chất và cũng như phương pháp giải các dạng toán liên quan đến số thực. Chúc các em học tốt.
Ngoài tài liệu trên, mời các em tham khảo thêm các tài liệu khác như Giải Vở BT Toán 7, Chuyên đề Toán 7 và các đề thi học kì 1 lớp 7, đề thi học kì 2 lớp 7 được cập nhật liên tục trên VnDoc để học tốt môn Toán hơn.
