16 Bài toán thực tế về thể tích
Toán lớp 11
Lớp:
Lớp 11
Môn:
Toán
Dạng tài liệu:
Chuyên đề
Loại File:
Word + PDF
Phân loại:
Tài liệu Tính phí
BÀI TOÁN THỰC TẾ HÌNH LĂNG TRỤ ĐỨNG, HÌNH CHÓP ĐỀU. THỂ TÍCH MỘT
SỐ HÌNH KHỐI.
A. KIẾN THỨC CẨN NHỚ
1. Hình lăng trụ đứng. Hình lăng trụ đều
Hình lăng trụ có cạnh bên vuông góc với mặt đáy được gọi là hình lăng trụ đứng.
Hình lăng trụ đứng có đáy là đa giác đều gọi là hình lăng trụ đều.
Hình lăng trụ đứng có đáy là hình bình hành được gọi là hình hộp đứng.
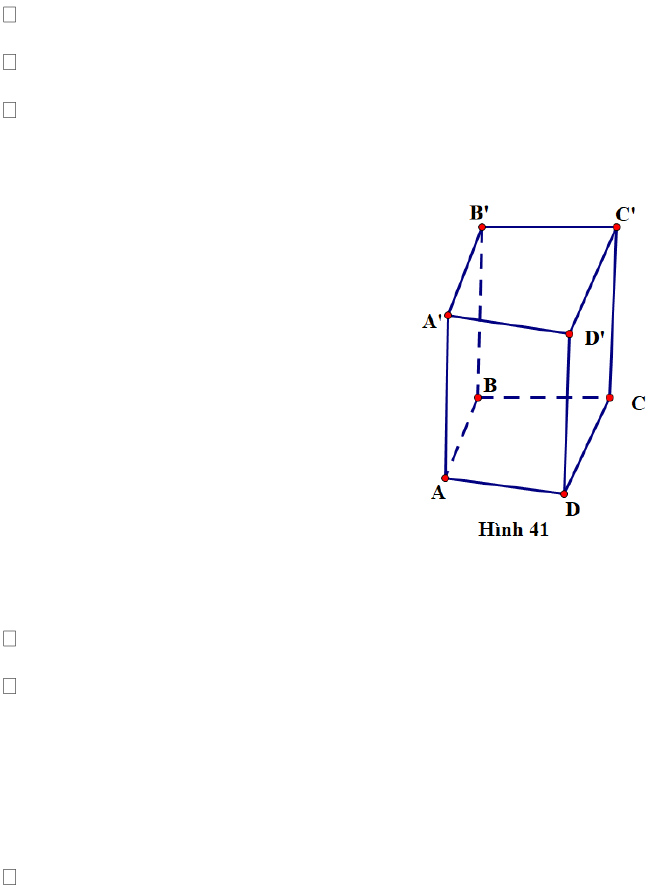
Ví dụ: Hình 41 biểu diễn hình lăng trụ đứng tứ giác
.ABCD ABCD
.
Nhận xét
Mỗi mặt bên của hình lăng trụ đứng là một hình chữ nhật, mặt phẳng chứa nó vuông góc với mặt đáy.
Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật.
Hình hộp chữ nhật có 6 mặt là hình chữ nhật.
Nếu mỗi mặt của hình hộp là hình chữ nhật thì hình hộp đó là hình hộp chữ nhật.
Độ dài các đường chéo của hình hộp chữ nhật là bằng nhau.
Hình lập phương là hình hộp chữ nhật có tất cả các mặt là hình vuông.
Hình lập phương là hình lăng trụ tứ giác đều có cạnh bên bằng cạnh đáy.
2. Hình chóp đều. Hình chóp cụt đều
a) Hình chóp đều
Hình chóp đều là hình chóp có đáy là đa giác đều và các cạnh bên bằng nhau.
Chú ý
Hình chóp tam giác đều có cạnh bên bằng cạnh đáy là tứ diện đều.
Đoạn thẳng nối đỉnh với hình chiếu của đỉnh trên mặt đáy là đường cao
Ví dụ: Hình 42 biểu diễn hình chóp tứ giác đều SABCD

b) Hình chóp cụt đều
Cho hình chóp đều
*
1 2 3
.
n
S A A A A
Mặt phẳng
P
song song với đáy của hình chóp và cắt các cạnh
12
, , ,
n
SA SA SA
lần lượt tại
12
, , ,
n
B B B
.
Phần của hình chóp đã cho giới hạn bởi hai mặt phẳng
P
và
1 2 3 n
A A A A
được gọi là hình chóp cụt
đều
1 2 1 2nn
A A A B B B
.
Trong hình chóp cụt đều
1 2 1 2nn
A A A B B B
, ta gọi:
- Các đa giác
1 2 1 2
,
nn
A A A B B B
lần lượt là đáy lớn, đáy nhỏ;
- Các tứ giác
1 2 2 1 2 3 3 2 1 1
, , ,
nn
A A B B A A B B A AB B
là các mặt bên;
- Các đoạn thẳng
1 1 2 2
, , ,
nn
AB A B A B
là các cạnh bên;
- Các cạnh của hai đa giác
1 2 1 2
,
nn
A A A B B B
là các cạnh đáy;
Ví dụ: Hình 43 biểu diễn hình chóp cụt tứ giác đều
41 2 3 1 2 34
.BA BA BA BA
Nhận xét:
- Hai đáy của hình chóp cụt đều nằm trên hai mặt phẳng song song và có các cạnh tương ứng song song:
đồng thời hai đáy đó là các đa giác đểu có cùng số cąnh;

- Mỗi mặt bên của hình chóp cụt đều là một hình thang cân;
- Các đường thẳng chứa cạnh bên của hình chóp cụt đều cùng đi qua một điểm;
- Đường cao của hình chóp cụt đều thì vuông góc với hai đáy của hình chóp cụt đều đó
3. Thể tích của một số hình khối
Phần không gian được giới hạn bởi một hình lăng trụ( kể cả hình lăng trụ ấy) được gọi là khối lăng trụ.
Các khối khác được định nghĩa tương tự.
a) Thể tích của khối lăng trụ
- Chiều cao của khối lăng trụ bằng khoảng cách giữa hai mặt đáy.
- Thể tích của khối lăng trụ được tính theo công thức:
, V Sh
trong đó
h
là chiều cao,
S
là diện tích
đáy của khối lăng trụ.
b) Thể tích của khối chóp
- Chiều cao của khối chóp bằng khoảng cách từ đỉnh đến mặt đáy.
- Thể tích của khối chóp được tính theo công thức:
1
,
3
V Sh
trong đó
h
là chiều cao,
S
là diện tích đáy
của khối chóp.
B. BÀI TẬP VẬN DỤNG
Câu 1: Quan sát và cho biết chiếc đèn treo ở Hình 96a, trạm khảo sát trắc địa ở Hình
96b
có dạng hình
gì.
Lời giải
Hình 96a có dạng hình khối lăng trụ
Hình 96b có dạng hình khối chóp cụt đều
Câu 2: Một chiếc bánh chưng có dạng khối hộp chữ nhật vởi kích thước ba cạnh là
15 cm
,
15 cm
và
6 cm
. Tính thể tích của chiếc bánh chưng đó.
Lời giải
Bài toán thực tế về thể tích lớp 11
16 Bài toán thực tế về thể tích là tài liệu hữu ích được VnDoc.com tổng hợp và xin gửi tới bạn đọc cùng tham khảo để có thêm tài liệu học tập môn Toán lớp 11 nhé. Bài viết được tổng hợp gồm có 2 phần: Lý thuyết nội dung kiến thức cần nhớ và bộ câu hỏi bài tập thực tế về thể tích. Bài viết có đáp án và lời giải chi tiết kèm theo. Mời các bạn cùng theo dõi chi tiết bài viết dưới đây nhé.


