Đề thi học kì 2 Toán 11 Kết nối tri thức - Đề 12
Thi học kì 2 lớp 11
Lớp:
Lớp 11
Môn:
Toán
Dạng tài liệu:
Đề thi
Bộ sách:
Kết nối tri thức với cuộc sống
Loại:
Tài liệu Lẻ
Loại File:
Word + PDF
Phân loại:
Tài liệu Tính phí
TRƯỜNG THPT ……..
KIỂM TRA CUỐI KỲ II - NĂM HỌC ……
Môn: TOÁN, Lớp 11
ĐỀ CHÍNH THỨC
Thời gian: 90 phút (Không kể thời gian phát đề)
Họ và tên thí sinh:.............................................................................. SBD:.....................
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Nghiệm của phương trình
3
log ( 2) 0x
là
A.
2x
. B.
5x
. C.
3x
. D.
3x
.
Câu 2. Cho tứ diện
OABC
có
,,OA OB OC
đôi một vuông góc với nhau và
1, 2, 3.OA OB OC
Thể tích
khối tứ diện
OABC
là
A.
3
. B.
6
. C.
2
. D.
1
.
Câu 3. Hai mặt phẳng vuông góc với nhau thì góc giữa hai mặt phẳng bằng:
A.
0
. B.
180
. C.
60
. D.
90
.
Câu 4. Cho hình lập phương
.ABCD ABCD
.Góc giữa hai đường thẳng nào sau đây bằng
0
.
A.
,A B CD
. B.
,C B A D
C.
,AD AB
D.
,CD AD
Câu 5. Cho
0a
, khi đó
2025
a
bằng
A.
5
1
202
a
. B.
2025
a
. C.
2025
1
a
. D.
2025
a
.
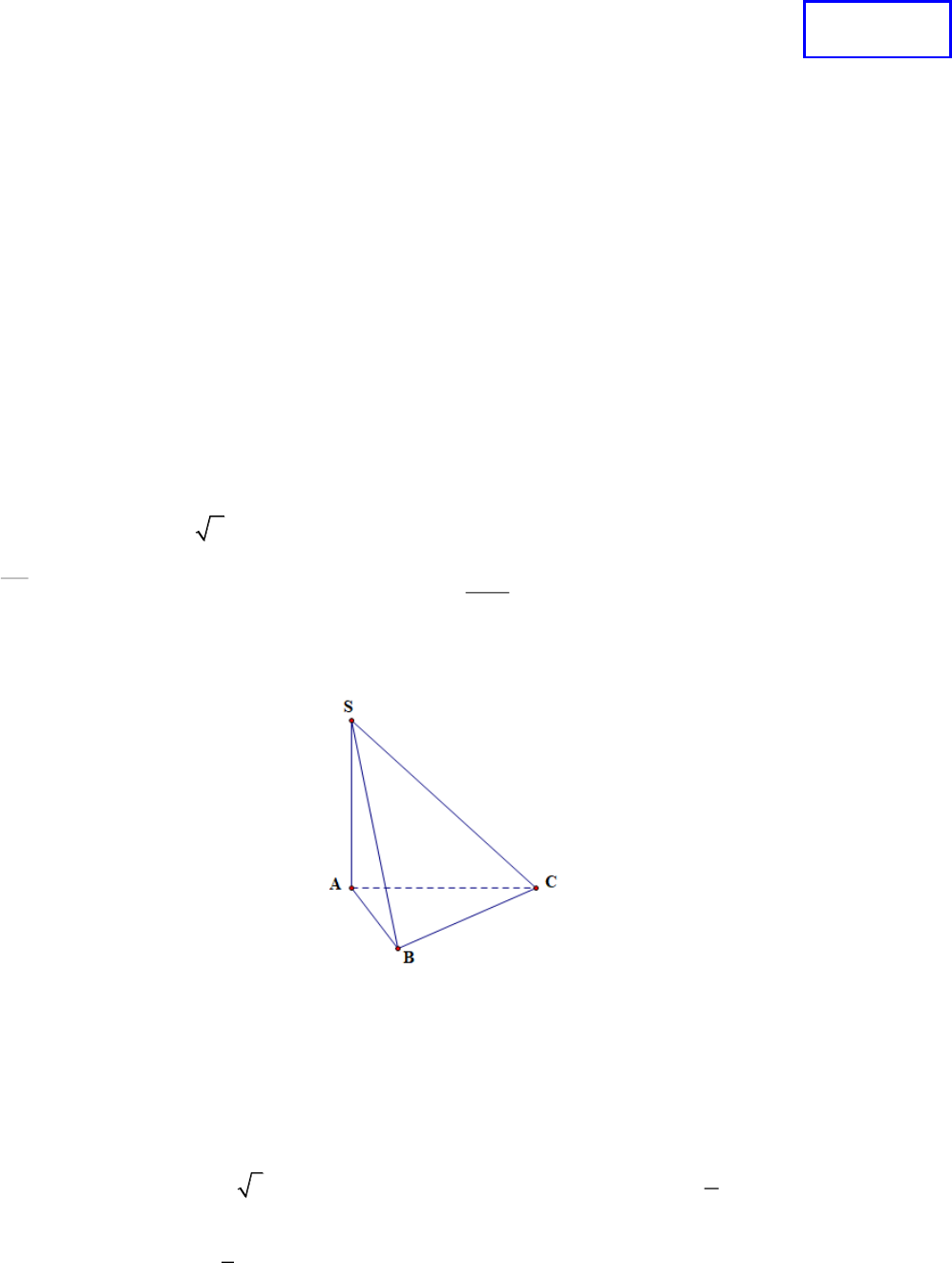
Câu 6. Cho hình chóp
.S ABC
có
SA
vuông góc với mặt phẳng
( )
,ABC
tam giác
ABC
vuông tại
B
.(minh
họa như hình vẽ bên).
.
Góc giữa đường thẳng
SC
và mặt phẳng
( )
ABC
là:
A.
·
SBC
. B.
·
SAC
. C.
·
SBA
. D.
·
SCA
.
Câu 7. Cho hình lập phương
. ' ' ' 'ABCD A B C D
cạnh bằng
a
. Khoảng cách giữa hai mặt phẳng
ABCD
và
AB C D
bằng
A.
2a
. B.
3a
. C.
a
. D.
2
a
.
Câu 8. Giải bất phương trình
2
3
21
1
3
3
x
x
ta được tập nghiệm là

A.
1
;
3
. B.
1
;1
3
.
C.
1;
. D.
1
; 1;
3
.
Câu 9. Chọn ngẫu nhiên một học sinh trong trường THPT Lê Quý Đôn. Gọi biến cố
A
: “Học sinh được
chọn bị cận thị” và biến cố
B
: “Học sinh được chọn học giỏi môn Toán”. Xác định biến cố
AB
.
A. Học sinh được chọn bị cận thị nhưng không học giỏi môn Toán.
B. Học sinh được chọn học giỏi môn Toán nhưng không bị cận thị.
C. Học sinh được chọn vừa bị cận thị vừa học giỏi môn Toán.
D. Học sinh được chọn bị cận thị hoặc học giỏi môn Toán.
Câu 10. Tập xác định của hàm số
5
x
y
là
A.
0;
. B. . C.
0;
. D.
\{0}
.
Câu 11. Cho đường cong
C
có phương trình
1
1
x
y
x
. Gọi
M
là giao điểm của
C
với trục tung. Tiếp
tuyến của
C
tại
M
có phương trình là
A.
21yx
. B.
21yx
. C.
2yx
. D.
21yx
.
Câu 12. Đạo hàm của hàm số
5 3 2
24y x x x
là
A.
42
' 10 12 2 .y x x x
B.
42
' 10 12 2 .y x x x
C.
42
' 10 3 2 .y x x x
D.
42
' 5 12 2 .y x x x
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Một người gửi
100
triệu đồng vào một ngân hàng với lãi suất
0,6%
/tháng. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn để tính lãi cho tháng tiếp theo
(thể thức lãi kép) và trong suốt thời gian gửi tiền người đó không rút tiền và lãi suất không thay đổi. Xét tính
đúng sai của các khẳng định sau:
a) Để thu được nhiều hơn 10 triệu tiền lãi, cần phải gửi ít nhất 16 tháng.
b) Sau 1 tháng, số tiền cả vốn lẫn lãi là 106 triệu đồng.
c) Sau
n
tháng, số tiền cả vốn lẫn lãi là:
1
100. 1 0,6%
n
(triệu đồng).
d) Sau 2 tháng, số tiền lãi thu được là 1.203.600 đồng.
Câu 2. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, mặt bên
SAB
là tam giác cân và
SAB ABCD
,
2SA a
. Gọi
I
,
H
lần lượt là trung điểm của
CD
và
AB
.
a) Khoảng cách từ
S
đến mặt phẳng
ABCD
là
15
2
a
. b) Khoảng cách từ
A
đến mặt phẳng
SBC
là
15
8
a
.

c) Khoảng cách từ
I
đến mặt phẳng
SHC
là
5
5
a
. d) Khoảng cách từ
D
đến mặt phẳng
SHC
là
2 15
5
a
.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Nếu một người gửi vào ngân hàng số tiền
P
với lãi suất
r
mỗi kì thì sau
N
kì, số tiền người đó
thu được được tính theo công thức lãi kép
1
N
A P r
. Ông Minh dự định gửi vào ngân hàng một số
tiền với lãi suất 6,5% một năm. Tính số tiền
x
mà ông Minh gửi vào ngân hàng để sau 3 năm số tiền lãi
vừa đủ mua một chiếc xe máy trị giá 60 triệu đồng .
Câu 2. Cho hình chóp
.S ABCD
có đáy là hình vuông tâm
O
, cạnh bằng
26a
,
SD ABCD
,
5SD a
.
Tính cô sin của góc giữa đường thẳng
SA
và mặt phẳng
SBD
,
Câu 3. Một chiếc ô tô với hai động cơ độc lập đang gặp trục trặc kĩ thuật. Xác suất để động cơ
1
gặp trục trặc
là
0,3
. Xác suất để động cơ
2
gặp trục trặc là
0,4
. Biết rằng xe chỉ không thể chạy được khi cả hai động cơ
bị hỏng. Khi đó xác suất để xe đi được là
Câu 4. Người ta xây dựng một cây cầu vượt giao thông hình parabol nối hai điểm có khoảng cách là
400 m
.
Độ dốc của mặt cầu không vượt quá
10
(độ dốc tại một điểm được xác định bởi góc giữa phương tiếp xúc
với mặt cầu và phương ngang). Tính chiều cao giới hạn từ đỉnh cầu đến mặt đường (làm tròn kết quả đến
hàng phần mười).
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Câu 1. Co
́
50 tâ
́
m the
̉
đa
́
nh sô
́
tư
̀
1 đê
́
n 50. Ru
́
t ngẫu nhiên 3 the
̉
. Tính xa
́
c suâ
́
t đê
̉
tô
̉
ng ca
́
c sô
́
ghi trên the
̉
chia hê
́
t cho 3.
Câu 2. Trong một phòng thí nghiệm, người ta nuôi một loại vi khuẩn. Lúc đầu có 300 vi khuẩn. Sau một giờ,
số vi khuẩn là
705
con. Giả sử số vi khuẩn tăng lên theo công thức tăng trưởng mũ, số vi khuẩn sau
x
giờ là
()
kx
f x C e
. Hỏi số vi khuẩn có được sau 5 giờ?
Câu 3. Cho khối lăng trụ đứng
.ABC ABC
có đáy
ABC
là tam giác vuông cân tại
B
. Biết
2C A a
và
45AC C
. Thể tích của khối lăng trụ đã cho bằng
Câu 4. Cho hình lăng trụ đứng
.
ABC ABC
có đáy
ABC
là tam giác vuông tại
A
,
AA AC a
và
3AB a
. Khoảng cách từ điểm
A
đến mặt phẳng
( ' )A BC
bằng
-------- HẾT--------
Đề thi học kì 2 môn Toán 11 cấu trúc mới
Để giúp bạn đọc có thêm tài liệu ôn thi kì thi học kì 2 lớp 11, VnDoc.com xin gửi tới bạn đọc bài viết Đề thi cuối học kì 2 Toán 11 Kết nối tri thức - Đề 12 có đáp án kèm theo để bạn đọc cùng tham khảo. Đề thi được biên soạn theo cấu trúc đề thi mới. Đề thi gồm có 12 câu hỏi trắc nghiệm nhiều phương án lựa chọn, 2 câu hỏi trắc nghiệm đúng sai, 4 câu hỏi trắc nghiệm trả lời ngắn và 4 câu hỏi tự luận. Thí sinh làm bài trong thời gian 90 phút. Đề có đáp án kèm theo. Mời các bạn cùng theo dõi đề thi dưới đây nhé.



