Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
VnDoc.com Lớp 9 Toán 9 Cánh diều

Giải Toán 9 trang 115 tập 1 Cánh diều

Giải Toán 9 trang 115 Tập 1

Giải Toán 9 trang 115 Tập 1 Cánh diều hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Cánh diều tập 1 trang 115.

Hoạt động 3 trang 115 Toán 9 Tập 1 Cánh diều

Trong Hình 55, đỉnh của góc AIB có thuộc đường tròn hay không? Hai cạnh của góc chứa hai dây cung nào của đường tròn?

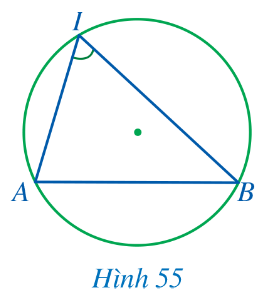
Hướng dẫn giải

Đỉnh của góc AIB là điểm I có thuộc đường tròn

Hai cạnh của góc AIB chứa hai dây cung IA, IB của đường tròn.

Luyện tập 3 trang 115 Toán 9 Tập 1 Cánh diều

Hãy vẽ một đường tròn và hai góc nội tiếp trong đường tròn đó.

Hướng dẫn giải

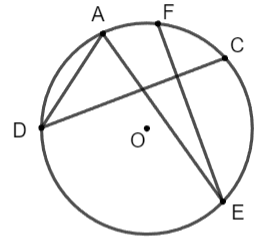
Hoạt động 4 trang 115 Toán 9 Tập 1 Cánh diều

Cho góc AIB nội tiếp đường tròn tâm O đường kính IK sao cho tâm O nằm trong góc đó (Hình 57).

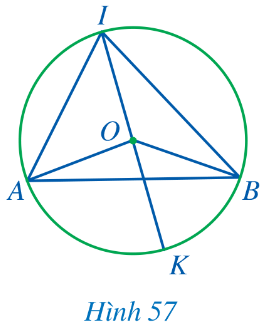
a) Các cặp góc \widehat {OAI} và \widehat {OIA},\widehat {OBI} và \widehat {OIB} có bằng nhau hay không?

b) Tính các tổng \widehat {AOI} + 2\widehat {OIA},\widehat {BOI} + 2\widehat {OIB}

c) Tính các tổng \widehat {AOI} + \widehat {AOK},\widehat {BOI} + \widehat {BOK}

d) So sánh \widehat {AOK} và 2\widehat {OIA},\widehat {BOK} và 2\widehat {OIB},\widehat {AOB} và 2\widehat {AIB}.

Hướng dẫn giải

a) Ta có IOA và IOB là các tam giác cân tại O

Suy ra \widehat {OAI} = \widehat {OIA} và \widehat {OBI} = \widehat {OIB}

b) Xét tam giác AOI cân tại O có:

\widehat {AOI} + \widehat {OIA} + \widehat {OAI} = 180^\circ (định lí tổng ba góc trong một tam giác)

\Rightarrow \widehat {AOI} + \widehat {OIA} + \widehat {OIA} = 180^\circ

Hay \widehat {AOI} + 2\widehat {OIA} = 180^\circ (1)

Tương tự ta có: \widehat {BOI} + 2\widehat {OIB} = 180^\circ (2) 

c) Do IK là đường kính nên:

\widehat {AOI} + \widehat {AOK} = 180^\circ (hai góc kề bù) (3)

\widehat {BOI} + \widehat {BOK} = 180^\circ (hai góc kề bù) (4)

d) Từ (1) và (3) suy ra 2\widehat {OIA} = \widehat {AOK} (*)

Từ (2) và (4) suy ra 2\widehat {OIB} = \widehat {BOK} (**)

Cộng vế với vế của (*) và (**), ta có:

2\left( {\widehat {OIA} + \widehat {OIB}} \right) =\widehat {AOK} + \widehat {BOK}

Hay 2\widehat {AIB} = \widehat {AOB}

-----------------------------------------------

---> Trang tiếp theo: Giải Toán 9 trang 116 tập 1 Cánh diều

Lời giải Toán 9 trang 115 Tập 1 Cánh diều với các câu hỏi nằm trong Bài 4: Góc ở tâm. Góc nội tiếp, được VnDoc biên soạn và đăng tải!

Chia sẻ, đánh giá bài viết
1
Bài viết đã được lưu
Mục lục
Tìm thêm: toán 9 giải toán 9 toán 9 cánh diều
Sắp xếp theo
Xóa Đăng nhập để Gửi
Toán lớp 9 Sách mới

Tham khảo thêm

Toán 9 Cánh diều
Xem thêm