Giải Toán 9 trang 116 tập 1 Cánh diều
Giải Toán 9 trang 116 Tập 1
Giải Toán 9 trang 116 Tập 1 Cánh diều hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Cánh diều tập 1 trang 116.
Luyện tập 4 trang 116 Toán 9 Tập 1 Cánh diều
Cho đường tròn (O; R) và dây cung AB = R. Điểm C thuộc cung lớn AB, C khác A và B. Tính số đo góc ACB.
Hướng dẫn giải
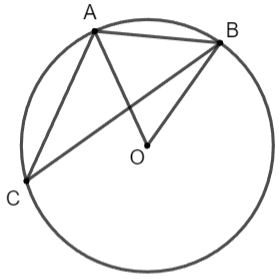
Xét tam giác OAB có OA = OB = AB = R
Do đó tam giác OAB là tam giác đều nên 
\(\widehat {AOB} = 60^\circ\)
Xét đường tròn (O):
Vì \(\widehat {AOB}\) là góc ở tâm và \(\widehat {ACB}\) là góc nội tiếp cùng chắn cung AB nên:
\(\widehat {ACB} = \frac{1}{2}\widehat {AOB} = \frac{1}{2}.60^\circ = 120^\circ\)
Hoạt động 5 trang 116 Toán 9 Tập 1 Cánh diều
Quan sát Hình 60 và nêu mối liên hệ giữa:
a) \(\widehat {AIB}\) và sđ \(\overset\frown{AmB}\)
b) \(\widehat {AKB}\) và sđ \(\overset\frown{AmB}\)
c) \(\widehat {AIB}\) và \(\widehat {AKB}\)
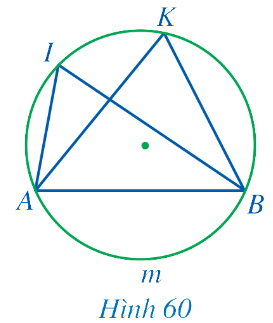
Hướng dẫn giải
a) Vì \(\widehat {AIB}\) là góc nội tiếp chắn cung AmB nên \(\widehat{AIB}=\frac{1}{2}sđ\overset\frown{AmB}\)
b) Vì \(\widehat {AKB}\) là góc nội tiếp chắn cung AmB nên \(\widehat{AKB}=\frac{1}{2}sđ\overset\frown{AmB}\)
c) Ta có \(\widehat {AIB} = \widehat {AKB}\) (\(=\frac{1}{2}sđ\overset\frown{AmB}\))
-----------------------------------------------
---> Trang tiếp theo: Giải Toán 9 trang 117 tập 1 Cánh diều
Lời giải Toán 9 trang 116 Tập 1 Cánh diều với các câu hỏi nằm trong Bài 4: Góc ở tâm. Góc nội tiếp, được VnDoc biên soạn và đăng tải!
