Hãy chỉ ra cặp tam giác đồng dạng với nhau từ các tam giác sau đây:
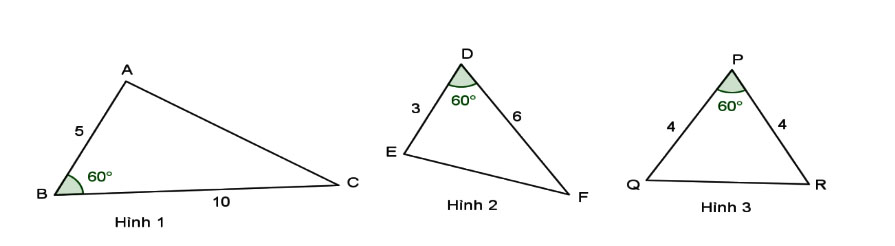
Ta có:
Xét tam giác ABC và tam giác EDF có:
Vndoc.com xin gửi tới bạn đọc bài Luyện tập về Ba trường hợp đồng dạng của hai tam giác lớp 8 sách Kết nối tri thức. Các câu hỏi được biên soạn bám sát chương trình, phù hợp cho ôn tập, kiểm tra và rèn luyện kỹ năng làm bài trắc nghiệm.
👇Mời bạn làm bài tập online dưới đây nhé!
Hãy chỉ ra cặp tam giác đồng dạng với nhau từ các tam giác sau đây:

Ta có:
Xét tam giác ABC và tam giác EDF có:
Cho tam giác ABC và MNP có kích thức như hình vẽ, hai tam giác có đồng dạng với nhau không, nếu có thì tỉ số đồng dạng bằng bao nhiêu?
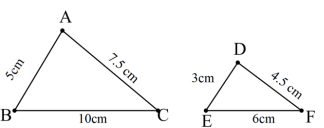
Ta có:
Cho tam giác ABC vuông tại A, kẻ đường cao AH. Hệ thức nào dưới đây là hệ thức đúng?
Xét tam giác HCA và tam giác HAB có:
Cho tam giác có
đồng dạng với tam giác
có
. Tìm tỉ số chu vi của hai tam giác ABC và MNP.
Ta có:
Lại có:
Tìm giá trị x trong hình vẽ. Biết AC = 9, AB = 6, BC = 10, DC = 13,5, AB // CD.
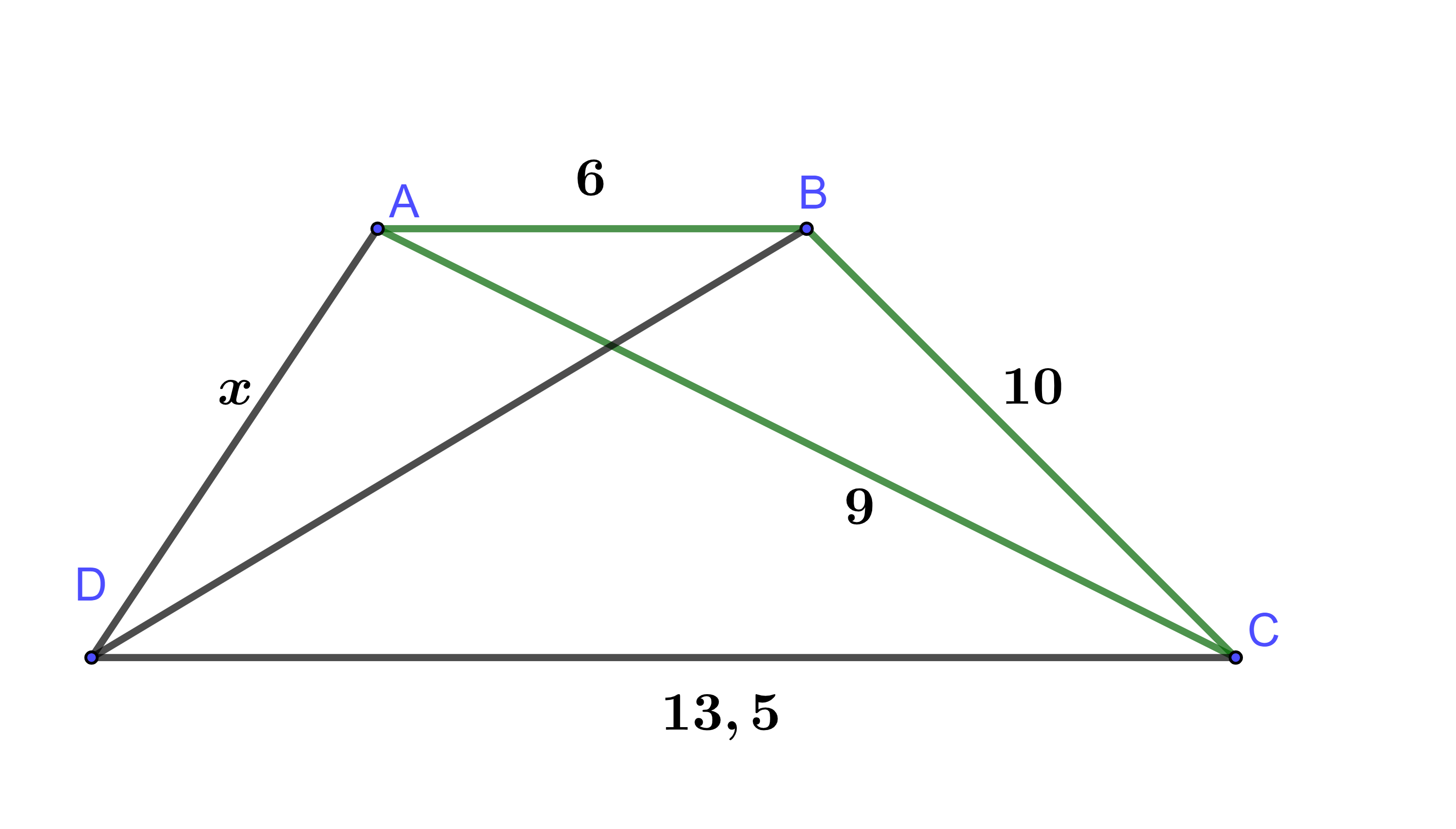
15
Tìm giá trị x trong hình vẽ. Biết AC = 9, AB = 6, BC = 10, DC = 13,5, AB // CD.

15
Ta có: AB // CD => (so le trong)
Lại có:
Xét tam giác ABC và tam giác CAD có:
Cho hình vẽ:
Chọn khẳng định đúng?
Ta có:
Trong các cặp tam giác sau cặp tam giác nào đồng dạng nếu các cạnh của hai tam giác có độ dài là:
Vì nên hai tam giác có độ dài các cạnh là 3 cm, 4 cm; 6 cm và 9cm, 15 cm, 18 cm không đồng dạng với nhau.
Vì nên hai tam giác có độ dài các cạnh là 4 cm, 5 cm; 6 cm và 8cm, 10 cm, 12 cm đồng dạng với nhau.
Vì nên hai tam giác có độ dài các cạnh là 6 cm, 5 cm; 6 cm và 3 cm, 5 cm, 3 cm không đồng dạng với nhau.
Vì nên hai tam giác có độ dài các cạnh là 5 cm, 7 cm; 1 dm và 10 cm, 14 cm, 18 cm không đồng dạng với nhau.
Xét tam giác ABC và tam giác DEF có: thì :
Xét tam giác ABC và tam giác DEF có:
Nên
Cho và
. Khi đó:
Vì suy ra:
Quan sát hình vẽ sau đây và cho biết khẳng định nào đúng?
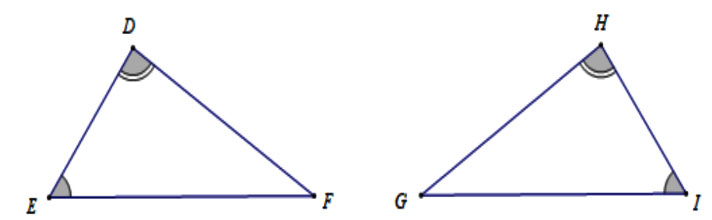
Xét tam giác HIG và tam giác DEF có:
Hãy chỉ ra cặp tam giác đồng dạng với nhau từ các tam giác sau đây:
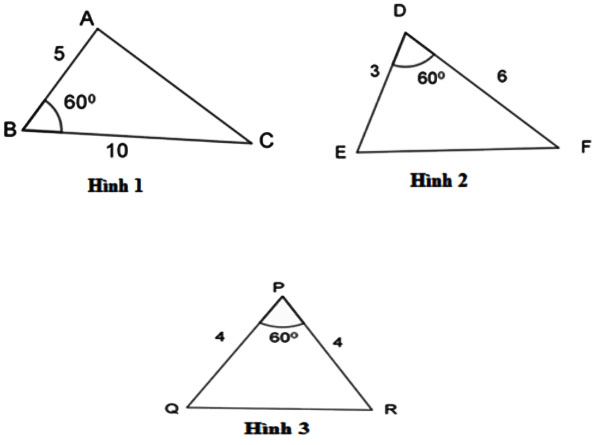
Ta có:
Xét tam giác ABC và tam giác EDF ta có:
Vậy cặp tam giác đồng dạng là Hình 1 và Hình 2.
Cho tam giác ABC, AC = b, AB = c. Kẻ đường phân giác AD có DB = m, DC = n. Kẻ tia Cx sao cho (Tia Cx khác phía với A đối với BC). Gọi I là giao điểm của AD và Cx. Khi đó AD2 bằng:
Hình vẽ minh họa
Xét tam giác ABD và tam giác CID ta có
Xét tam giác ABD và tam giác AIC ta có:
Từ (*) và (**) suy ra
Cho tam giác ABC (AB < AC). Kẻ đường phân giác AD. Đường trung trực của AD cắt BC ở K. Biết rằng BA = 2 cm, DC = 4 cm. Tính độ dài cạnh KD?
Kết quả: 4cm
Cho tam giác ABC (AB < AC). Kẻ đường phân giác AD. Đường trung trực của AD cắt BC ở K. Biết rằng BA = 2 cm, DC = 4 cm. Tính độ dài cạnh KD?
Kết quả: 4cm
Hình vẽ minh họa
Do K thuộc đường trung trực của AD nên KA = KD.
Suy ra tam giác KAD cân tại K
(
là góc ngoài tại đỉnh D của tam giác DAC)
Mà (AD là phân giác tam giác ABC) nên
Xét tam giác KAB và tam giác KCA ta có:
Góc chung
Mà (AD là phân giác tam giác ABC)
mà
Cho hình thang ABCD có (AB // CD), Giao điểm hai đường chéo tại O. Khẳng định nào dưới đây đúng?
Hình vẽ minh họa

Vì AB // CD nên
Xét tam giác OAB và tam giác OCD có:
Cho tam giác ABC, lấy hai điểm D và E lần lượt nằm trên các cạnh AB và AC sao cho . Kết luận nào sau đây sai?
Hình vẽ minh họa

Xét tam giác ADE và tam giác ABC có:
Góc A chung
Cho tam giác ABC có . Trên cạnh AB và AC lần lượt lấy các điểm M và N sao cho
. Xác định độ dài đoạn thẳng MN.
Kết quả: 5 cm
Cho tam giác ABC có . Trên cạnh AB và AC lần lượt lấy các điểm M và N sao cho
. Xác định độ dài đoạn thẳng MN.
Kết quả: 5 cm
Hình vẽ minh họa

Ta có:
Xét tam giác ANM và tam giác ABC có :
Góc A chung
Cho hình vẽ:
Chọn khẳng định đúng?
Ta có:
Mà hai góc ở vị trí đồng vị
Cho hình vẽ sau:
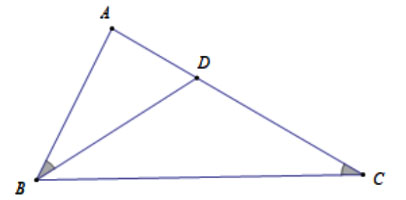
Biết . Độ dài đoạn thẳng AD là:
Xét tam giác ABC và tam giác ADB ta có:
Góc A chung
Hai tam giác đồng dạng với nhau theo trường hợp cạnh - góc - cạnh nếu
Hai tam giác đồng dạng với nhau theo trường hợp cạnh - góc - cạnh nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau.
Cho tam giác có
và tam giác
có
. Khẳng định nào sau đây đúng?
Ta có:
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
