Đại cương về đường thẳng và mặt phẳng
a) Để biểu diễn một mặt phẳng ta thường dùng hình bình hành hay một miền góc. Kí hiệu mặt
phẳng: dùng chữ cái in hoa hoặc chữ cái Hi Lạp đặt trong dấu ngoặc đơn. Ví dụ: mặt phẳng 
\((P)\), mặt phẳng \((α)\) hoặc viết tắt là \(mp(P), mp(α)\) hoặc \((P), (α), . . .\)
b) Điểm \(A\) thuộc mặt phẳng \((P)\) kí hiệu là \(A \in (P)\).
Điểm \(B\) không thuộc mặt phẳng \((P)\) kí hiệu là \(B \notin(P)\).
Quy tắc vẽ hình không gian:
- Hai đường song song vẽ thành hai đường song song, hai đường cắt nhau vẽ thành hai đường
cắt nhau. - Giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.
- Dùng nét liền để vẽ đường nhìn thấy; dùng nét đứt để vẽ đường bị che khuất.
2. Các tính chất thừa nhận
Tính chất 1. Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
Tính chất 2. Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.
Tính chất 3. Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
Tính chất 4. Tồn tại bốn điểm không cùng thuộc một mặt phẳng.
Tính chất 5. Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung
khác nữa.
Tính chất 6. Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.
3. Cách xác định một mặt phẳng
Có ba cách xác định một mặt phẳng:
a) Khi biết mặt phẳng đi qua ba điểm không thẳng hàng.
b) Khi biết mặt phẳng đi qua một điểm và chứa một đường thẳng không đi qua điểm đó.
c) Khi biết mặt phẳng chứa hai đường thẳng cắt nhau.
Chú ý:
- Để chứng minh ba điểm thẳng hàng ta có thể chứng minh chúng cùng thuộc hai mặt phẳng phân biệt.
- Để tìm giao điểm của một đường thẳng và một mặt phẳng ta có thể đưa về việc tìm giao điểm của đường thẳng đó với một đường thẳng nằm trong mặt phẳng đã cho.
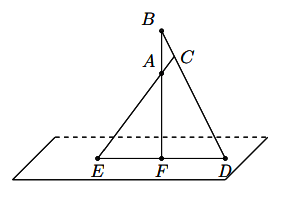
Ví dụ: Cho mặt phẳng \((α)\) và ba điểm \(A, B, C\) không thẳng hàng nằm ngoài mặt phẳng \((α)\). Giả sử các đường thẳng \(BC, CA, AB\) lần lượt cắt \((α)\) tại \(D, E, F\). Chứng minh ba điểm \(D, E, F\) thẳng hàng.
Hướng dẫn giải
Hình vẽ minh họa
Ta có: \(\left\{ {\begin{array}{*{20}{l}}
{E,F,D \in \left( {ABC} \right)} \\
{E,F,D \in \left( \alpha \right)}
\end{array}} \right.\)
=> \(D, E, F\) thuộc giao tuyến của \((ABC)\) và \((α)\)
Vậy \(D, E, F\) thẳng hàng.
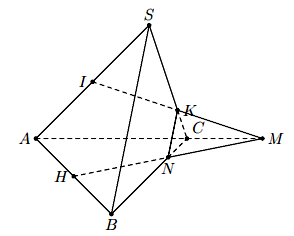
Ví dụ: Cho hình chóp \(S.ABC\). Gọi I là trung điểm của cạnh \(SA\), \(H\) là trung điểm của cạnh\(AB\), \(K\) là điểm trên cạnh \(SC\) sao cho \(SC = 4KC\).
a) Tìm giao điểm \(M\) của \(IK\) và mặt phẳng \((ABC)\).
b) Tìm giao điểm \(N\) của \(HM\) và mặt phẳng \((SBC)\).
Hướng dẫn giải
Hình vẽ minh họa
a) Gọi \(M = IK ∩ AC\). Ta có: \(M ∈ IK\) và \(M ∈ AC ⊂(ABC)\).
Suy ra \(M = IK ∩ (ABC)\).
b) Gọi \(N = HM ∩ BC\). Ta có: \(N ∈ HM\) và \(N ∈ BC ⊂(SBC)\).
Suy ra \(N = HM ∩ (SBC)\).
4. Giao tuyến của hai mặt phẳng
- Giả sử \((P), (Q)\) là hai mặt phẳng phân biệt có điểm chung \(A\). Khi đó \((P), (Q)\) có đường thẳng chung duy nhất \(d\) đi qua \(A\). Đường thẳng \(d\) được gọi là giao tuyến của hai mặt phẳng.
- Đường thẳng \(d\) được gọi là giao tuyến của hai mặt phẳng \((P), (Q)\), kí hiệu \(d=(P)\cap (Q)\).
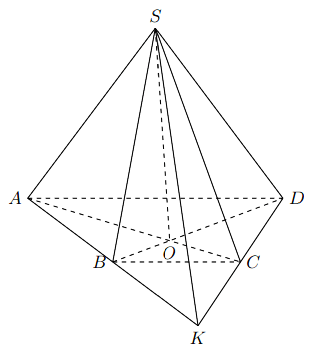
Ví dụ: Cho tứ giác \(ABCD\) có cặp cạnh đối \(AB, CD\) không song song với nhau và \(S\) là điểm
không nằm trên mặt phẳng \((ABCD)\). Tìm giao tuyến của các cặp mặt phẳng \((SAC)\) và \((SBD)\), \((SAB)\) và \((SCD)\).
Hướng dẫn giải
Hình vẽ minh họa
Ta có: \(\left\{ {\begin{array}{*{20}{l}}
{S \in \left( {SAC} \right)} \\
{S \in \left( {SBD} \right)}
\end{array}} \right.\)(1)
Gọi O là giao điểm của AC và BD, khi đó do \(O ∈ BD\)
=> \(O ∈ (SBD)\). Tương tự ta có \(O ∈ (SAC)\). (2)
Từ (1) và (2) => SO là giao tuyến của hai mặt phẳng (SAC) và (SBD).
Gọi K là giao điểm của AB và CD, khi đó ta có \(\left\{ {\begin{array}{*{20}{l}}
{K \in \left( {SAB} \right)} \\
{K \in \left( {SCD} \right)}
\end{array}} \right.\)(3)
Mặt khác \(\left\{ {\begin{array}{*{20}{l}}
{S \in \left( {SAB} \right)} \\
{S \in \left( {SCD} \right)}
\end{array}} \right.\) (4)
Từ (3) và (4) => SK là giao tuyến của hai mặt phẳng (SAB) và (SCD).
5. Hình chóp và hình tứ diện
a) Trong mặt phẳng \((α)\) cho đa giác A1A2...An. Lấy điểm S ở ngoài \((α)\) và nối S với tất cả các đỉnh của đa giác A1A2...An. Hình gồm đa giác A1A2...An và n tam giác SA1A2, SA2A3, . . . , SAnA1 gọi là hình chóp và kí hiệu là S.A1A2...An.
b) Hình chóp tam giác S.ABC còn gọi là tứ diện SABC.
c) Thiết diện (hay mặt cắt) của hình \(H\) khi cắt mặt phẳng \((α)\) là phần chung của \(H\) và \((α)\)
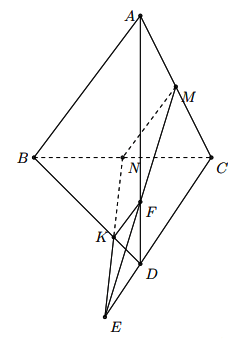
Ví dụ: Cho tứ diện \(ABCD\), \(M, N\) lần lượt là trung điểm của \(AC, BC\). Lấy \(K ∈ BD\) sao cho \(BK = 3KD\). Xác định thiết diện của (MNK) với tứ diện.
Hướng dẫn giải
Hình vẽ minh họa
Ta có \(\left\{ {\begin{array}{*{20}{l}}
{M,{\text{ }}N \in \left( {MNK} \right)} \\
{M,{\text{ }}N \in \left( {ABC} \right)} \\
{M \ne N}
\end{array}} \right. \Rightarrow \left( {MNK} \right) \cap \left( {ABC} \right) = MN\)
Trong \(mp(BDC)\), kẻ \(NK ∩ CD = E\), \(E ∈ NK\)
\(⇒ E ∈ mp(MNK)\)
Trong \(mp(ACD)\), kẻ \(ME∩AD = F, F ∈ ME\)
\(⇒ F ∈ mp(MNK)\)
Vậy thiết diện cần tìm là tứ giác MNKF.
