Phép tịnh tiến
Định nghĩa
Trong mặt phẳng có vectơ 
\(\vec{v}\). Phép biến hình biến mỗi điểm \(M\) thành điểm \(M'\) sao cho \(\vec{MM'} =\vec{v}\) được gọi là phép tịnh tiến theo vecto \(\vec{v}\).
Hình vẽ minh họa
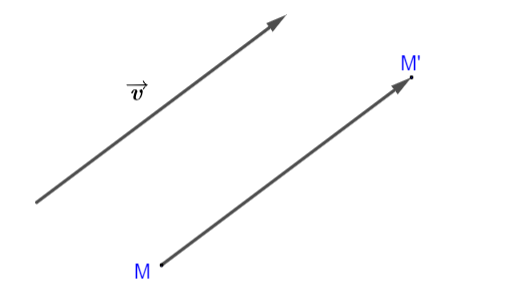
Phép tịnh tiến theo vectơ \(\vec{v}\) thường được kí hiệu là \(T_\vec{v}\), \(\vec{v}\) được gọi là vectơ tịnh tiến.
Như vậy: \(T_\vec{v} (M)=M'\Leftrightarrow \vec{MM'}=\vec{v}\)
Ví dụ: Cho hình bình hành \(ABCD\). Dựng ảnh của tam giác \(ABC\) qua phép tịnh tiến theo
vecto \(\overrightarrow {AD}\)
Hướng dẫn giải
Hình vẽ minh họa
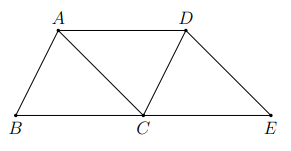
Vì \(\overrightarrow {AD} \ne \overrightarrow {BC}\) nên phép tịnh tiến theo \(\overrightarrow {AD}\) biến điểm \(A\) thành điểm \(D\), biến điểm \(B\) thành \(C\).
Để tìm ảnh của \(C\) ta dựng hình bình hành \(ADEC\).
Khi đó ta có ảnh của điểm \(C\) là điểm \(E\).
Vậy ảnh của tam giác \(ABC\) qua phép tịnh tiến theo \(\overrightarrow {AD}\) là tam giác \(DCE\).
2. Tính chất của phép tịnh tiến
Phép tịnh tiến là một phép biến hình bảo toàn khoảng cách.
\({T_{\vec v}}(M) = M',{T_{\vec v}}(N) = N'\)
\(\Rightarrow \overrightarrow {M'N'} = \overrightarrow {MN}\)
\(\Rightarrow \left| {\overrightarrow {MN} } \right| = \left| {\overrightarrow {M'N'} } \right|\)
\(\Rightarrow MN = M'N'\)
Hình vẽ minh họa
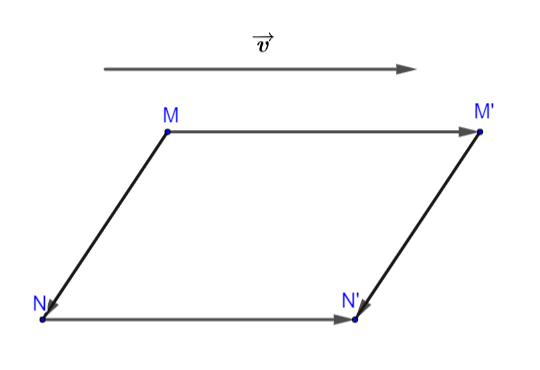
Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.
Hình vẽ minh họa
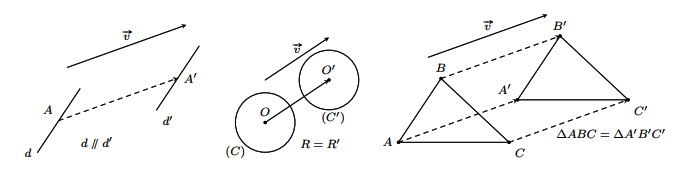
3. Biểu thức tọa độ của phép tịnh tiến
Trong mặt phẳng tọa độ Oxy cho vecto \(\vec{v} =(a,b)\). Với mỗi điểm \(M\left(x,y\right)\) ta có \(M'\left(x',\ y'\right)\) là ảnh của điểm \(M\) qua phép tịnh tiến \(\overrightarrow v\). Khi đó:
\(M'=T_\vec{v} (M)\Leftrightarrow \left\{\begin{matrix} x'=x+a \\ y'=y+b \end{matrix}\right.\)
Biểu thức trên được gọi là biểu thức tọa độ của phép tịnh tiến \({T_{\overrightarrow v }}\)
Ví dụ: Trong mặt phẳng tọa độ Oxy cho vecto \(\overrightarrow v =(-1;2)\), hai điểm \(A(3; 5), B(−1; 1)\) và
đường thẳng \(d\) có phương trình \(x − 2y + 3 = 0\).
a) Tìm tọa độ của \(A', B'\) theo thứ tự là ảnh của \(A, B\) qua phép tịnh tiến theo \(\overrightarrow v\).
b) Tìm tọa độ của điểm \(C\) sao cho \(A\) là ảnh của \(C\) qua phép tịnh tiến theo \(\overrightarrow v\).
c) Tìm phương trình của đường thẳng \(d'\) là ảnh của \(d\) qua phép tịnh tiến theo \(\overrightarrow v\).
Hướng dẫn giải
a) Tọa độ điểm \(A'\) là: \(\left\{ {\begin{array}{*{20}{c}}
{{x_{A'}} = 3 + \left( { - 1} \right) = 2} \\
{{y_{A'}} = 5 + 2 = 7}
\end{array}} \right. \Rightarrow A'\left( {2;7} \right)\).
Tọa độ điểm \(B'\) là: \(\left\{ {\begin{array}{*{20}{c}}
{{x_{B'}} = - 1 + \left( { - 1} \right) = - 2} \\
{{y_{B'}} = 1 + 2 = 3}
\end{array}} \right. \Rightarrow B'\left( { - 2;3} \right)\)
b) Giả sử điểm \(C\left( {{x_C};{y_C}} \right)\) sao cho \(A\) là ảnh của \(C\) qua phép tịnh tiến \(\overrightarrow v\). Khi đó ta có:
\(\left\{ {\begin{array}{*{20}{c}}
{3 = {x_{B'}} + \left( { - 1} \right)} \\
{5 = {y_{B'}} + 2}
\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{{x_{B'}} = 4} \\
{{y_{B'}} = 3}
\end{array}} \right. \Rightarrow C\left( {4;3} \right)\)
c) Giả sử \({M\left( {x;y} \right) \in d}\) và \({M'\left( {x';y'} \right)}\) là ảnh của qua phép tịnh tiến \(\overrightarrow v\). Khi đó ta có:
\(\left\{ {\begin{array}{*{20}{c}}
{x' = x - 1} \\
{y' = y + 2}
\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{x = x' + 1} \\
{y = y' - 2}
\end{array}} \right.\)
\(\Rightarrow M'\left( {x' + 1;y' - 2} \right)\)
Vì \(M \in d\) nên \(x' + 1 - 2\left( {y' - 2} \right) + 3 = 0\)
\(\Rightarrow x' - 2y' + 8 = 0\)
\(\Rightarrow d':x - 2y + 8 = 0\)
