Nhị thức Newton
Định lí
Với 
\(\forall n\in {{\mathbb{N}}^{*}}\) với cặp số \(\left( a,b \right)\) ta có:
\({{\left( a+b \right)}^{n}}=\sum\limits_{k=0}^{n}{C_{n}^{k}{{a}^{n-k}}}{{b}^{k}}=C_{n}^{0}{{a}^{n}}+C_{n}^{1}{{a}^{n-1}}b+C_{n}^{2}{{a}^{n-2}}{{b}^{2}}+...+C_{n}^{n-1}{{a}^{1}}{{b}^{n-1}}+C_{n}^{n}{{b}^{n}}\)
Hệ quả
\({{\left( 1+x \right)}^{n}}=C_{n}^{0}+xC_{n}^{1}+{{x}^{2}}C_{n}^{2}+...+{{x}^{n}}C_{n}^{n}\)
- Với \(a=b=1\) ta có \({{2}^{n}}=C_{n}^{0}+C_{n}^{1}+C_{n}^{2}+...+C_{n}^{n}\)
- Với \(a=1;b=-1\)\(C_{n}^{0}-C_{n}^{1}+C_{n}^{2}-C_{n}^{3}+...+{{\left( -1 \right)}^{n}}C_{n}^{n}=0\)
Chú ý: Trong khai triển Newton \({{\left( a+b \right)}^{n}}\) có tính chất sau:
- Gồm n + 1 phần tử.
- Số mũ của a giảm từ n đến 0 và số mũ của b tăng từ 0 đến n.
- Tổng số mũ của a và b trong mỗi số hạng bằng n .
- Các hệ số có tính đối xứng \(C_{n}^{k}=C_{n}^{n-k},\left( 0\le k\le n \right)\).
- Số hạng tổng quát: \({{T}_{k+1}}=C_{n}^{k}{{a}^{b-k}}{{b}^{k}}\)
- Số hạng thứ nhất \({{T}_{1}}={{T}_{0+1}}=C_{n}^{0}{{a}^{n}}\)
- Số hạng thứ k: \({{T}_{k}}={{T}_{k-1+1}}=C_{n}^{k-1}{{a}^{n-k+1}}{{b}^{k-1}}\)
Ví dụ 1: Viết khai triển theo công thức nhị thức Newton:
| \(a, {{\left( a+2b \right)}^{5}}\) |
\(b, {{\left( a-\sqrt{2} \right)}^{6}}\) |
Hướng dẫn giải
a. Khai triển Newton của \({{\left( a+2b \right)}^{5}}\)
\({{\left( a+2b \right)}^{5}}=\sum\limits_{k=0}^{5}{C_{5}^{k}{{a}^{5-k}}{{\left( 2b \right)}^{k}}}=\sum\limits_{k=0}^{5}{C_{5}^{k}{{a}^{5-k}}{{.2}^{k}}.{{b}^{k}}}\)
\({{\left( a+2b \right)}^{5}}=C_{5}^{0}{{a}^{5}}+C_{5}^{1}{{a}^{4}}2b+...+C_{5}^{5}32{{b}^{5}}\)
b. Khai triển Newton của \({{\left( a-\sqrt{2} \right)}^{6}}\)
\({{\left( a-\sqrt{2} \right)}^{6}}=\sum\limits_{k=0}^{6}{C_{6}^{k}{{a}^{6-k}}{{\left( \sqrt{2} \right)}^{k}}}\)
\({{\left( a-\sqrt{2} \right)}^{6}}=C_{6}^{0}{{a}^{6}}+C_{6}^{1}{{a}^{5}}.\sqrt{2}+C_{6}^{2}{{a}^{4}}.2+...+C_{6}^{6}.{{\left( \sqrt{2} \right)}^{6}}\)
Ví dụ 2: Tìm hệ số của \({{x}^{7}}\) trong khai triển biểu thức \({{\left( 1-2x \right)}^{10}}\)
Hướng dẫn giải
Ta có: \(f\left( x \right)={{\left( 1-2x \right)}^{10}}=\sum\limits_{k=0}^{10}{C_{10}^{k}{{.1}^{10-k}}{{\left( -2x \right)}^{k}}=}\sum\limits_{k=0}^{10}{C_{n}^{k}.{{\left( -2 \right)}^{k}}.{{x}^{k}}}\)
Số hạng chứa \({{x}^{7}}\) trong khai triển ứng với k = 7. Khi đó hệ số của số hạng chứa \({{x}^{7}}\):
\(C_{10}^{7}.{{\left( -2 \right)}^{7}}=-15360\)
Ví dụ 3: Tìm hệ số không chứa x trong khai triển sau: \({{\left( {{x}^{3}}-\frac{2}{x} \right)}^{n}}\)biết rằng:
\(C_{n}^{n-1}+C_{n}^{n-2}=78,x>0\)
Hướng dẫn giải
Ta có: \(C_{n}^{n-1}+C_{n}^{n-2}=78,n>2\)
\(\Leftrightarrow \frac{n!}{\left( n-1 \right)!(n-n+1)!}+\frac{n!}{\left( n-2 \right)!\left( n-2+2 \right)!}=78\)
\(\Leftrightarrow \frac{n!}{\left( n-1 \right)!(1)!}+\frac{n!}{\left( n-2 \right)!\left( 2 \right)!}=78\)
\(\Leftrightarrow n+\frac{n\left( n-1 \right)}{2}=78\Leftrightarrow {{n}^{2}}+n-156=0\Leftrightarrow \left[ \begin{matrix}
n=12\left( TM \right) \\
n=-13\left( L \right) \\
\end{matrix} \right.\)
Do đó biểu thức khai triển là \({{\left( {{x}^{3}}-\frac{2}{x} \right)}^{12}}=\sum\limits_{k=0}^{12}{C_{12}^{k}{{\left( {{x}^{3}} \right)}^{12-k}}{{\left( -\frac{2}{x} \right)}^{k}}}\)
\(=\sum\limits_{k=0}^{12}{C_{12}^{k}.{{x}^{36-3k}}.{{\left( \frac{1}{x} \right)}^{k}}.{{\left( -2 \right)}^{k}}}=\sum\limits_{k=0}^{12}{C_{12}^{k}.{{x}^{36-4k}}.{{\left( -2 \right)}^{k}}}\)
Số hạng không chứa x ứng với k: \(36-4k=0\Leftrightarrow k=9\)
Số hạng không chưa x là: \(C_{12}^{9}.{{\left( -2 \right)}^{9}}=-112640\)
Ví dụ 4: Xét khai triển: \({{\left( 2x+\frac{1}{x} \right)}^{20}}\)
a. Viết số hạng thứ k + 1 trong khai triển.
b. Số hạng nào trong khai triển không chứa x.
c. Xác định hệ số của \({{x}^{4}}\) trong khai triển.
Hướng dẫn giải
\({{\left( 2x+\frac{1}{x} \right)}^{20}}=\sum\limits_{k=0}^{20}{C_{20}^{k}{{\left( 2x \right)}^{20-k}}{{\left( \frac{1}{x} \right)}^{k}}=}\sum\limits_{k=0}^{20}{C_{20}^{k}{{2}^{20-k}}{{x}^{20-2k}}}\)
Số hạng không chứa x trong khai triển ứng với k là: \(20-2k=0\Leftrightarrow k=10\)
Số hạng không chứa x trong khai triển là: \(C_{20}^{10}{{.2}^{10}}\)
Số hạng chứa \({{x}^{4}}\) trong khai triển ứng với k là: \(20-2k=4\Leftrightarrow k=8\)
Vậy số hạng chứa \({{x}^{4}}\) trong khai triển có hệ số là: \(C_{20}^{8}{{.2}^{12}}\)
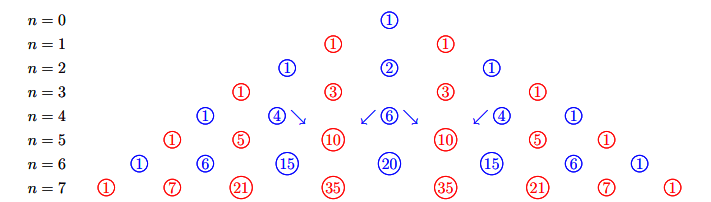
II. Tam giác Pascal
Trong công thức nhị thức Newton, cho \(n=0,1,...\) và sắp xếp các hệ số thành dòng, ta nhận được tam giác sau đây, gọi là tam giác Pascal.
Ví dụ 5: Tính tổng: \(S=\frac{1}{2}C_{n}^{0}-\frac{1}{4}c_{n}^{1}+\frac{1}{6}C_{n}^{3}-\frac{1}{8}C_{n}^{4}+...+\frac{\left( -1 \right)}{2\left( n+1 \right)}C_{n}^{n}\)
Hướng dẫn giải
Ta có: \(S=\frac{1}{2}\left( C_{n}^{0}-\frac{1}{2}c_{n}^{1}+\frac{1}{3}C_{n}^{3}-\frac{1}{4}C_{n}^{4}+...+\frac{\left( -1 \right)}{n+1}C_{n}^{n} \right)\)
Vì \(\frac{{{\left( -1 \right)}^{k}}}{k+1}C_{n}^{k}=\frac{{{\left( -1 \right)}^{k}}}{k+1}C_{n+1}^{k+1}\)
\(\begin{matrix}
\Leftrightarrow S = \dfrac{1}{{2\left( {n + 1} \right)}}\sum\limits_{k = 0}^n {{{\left( { - 1} \right)}^k}C_{n + 1}^{k + 1}} \hfill \\
= \dfrac{{ - 1}}{{2\left( {n + 1} \right)}}\left( {\sum\limits_{k = 0}^{n + 1} {{{\left( { - 1} \right)}^k}C_{n + 1}^k - C_{n + 1}^0} } \right) \hfill \\
= \dfrac{1}{{2\left( {n + 1} \right)}} \hfill \\
\end{matrix}\)
