Hai đường thẳng chéo nhau và hai đường thẳng song song
Cho hai đường thẳng 
\(a, b\) trong không gian, có 2 trường hợp xảy ra:
Trường hợp 1: \(a, b\) đồng phẳng
Hình vẽ minh họa
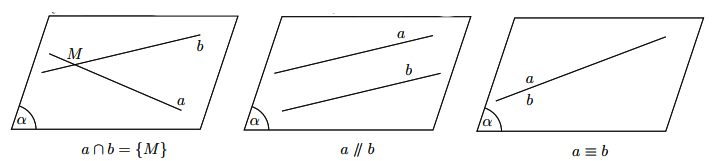
- \(a\) và \(b\) có điểm chung duy nhất \(M\), ta nói \(a\) và \(b\) cắt nhau tại \(M\) và kí hiệu là \(a ∩ b = {M}\) hay\(a ∩ b = M\).
- \(a\) và \(b\) không có điểm chung. Ta nói \(a\) và \(b\) song song với nhau, kí hiệu là \(a // b\).
- \(a\) trùng \(b\), kí hiệu \(a ≡ b\).
Chú ý: Hai đường thẳng song song là hai đường thẳng cùng nằm trong một mặt phẳng và không có điểm chung.
Trường hợp 2: \(a, b\) không đồng phẳng
Hình vẽ minh họa
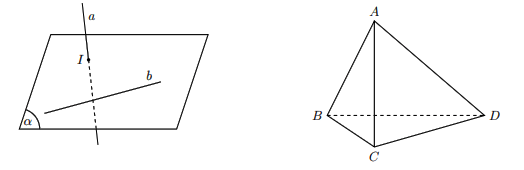
Theo hình vẽ ở trên ta nói \(a, b\) chéo nhau hoặc \(a\) chéo với \(b\)
Tứ diện ABCD có các cặp đường thẳng chéo nhau là AB và CD; BC và AD; AC và BD.
II. Tính chất của hai đường thẳng song song
Dựa vào tiên đề Ơ – clít về hai đường thẳng song song trong mặt phẳng ta có:
Định lí
Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng cho trước.
Hình vẽ minh họa
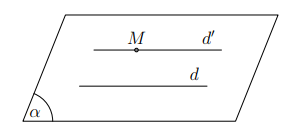
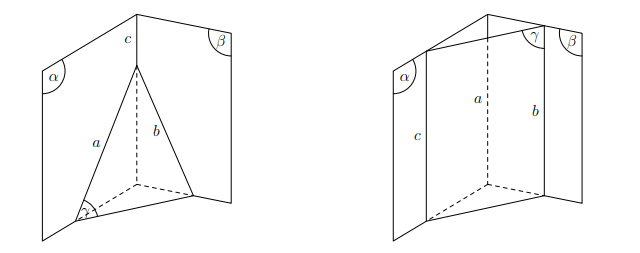
Định lí (giao tuyến của ba mặt phẳng)
Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.
Hình vẽ minh họa
Chú ý: Hai đường thẳng song song \(a\) và \(b\) xác định một mặt phẳng, kí hiệu là \(mp (a, b)\) hay \((a, b)\).
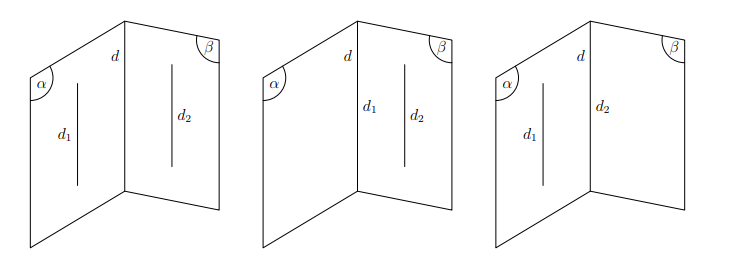
Hệ quả
Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Hình vẽ minh họa
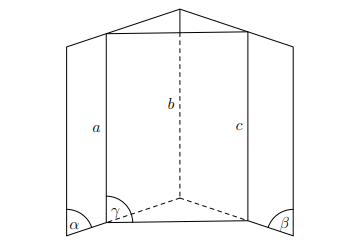
Định lí
Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
Hình vẽ minh họa
Ví dụ: Cho tứ diện ABCD. Gọi M, N theo thứ tự là trung điểm của AB, BC và Q là một
điểm nằm trên cạnh AD (QA ≠ QD) và P là giao điểm của CD với mặt phẳng (MNQ). Chứng
minh rằng PQ // MN và P Q // AC.
Hướng dẫn giải
Hình vẽ minh họa
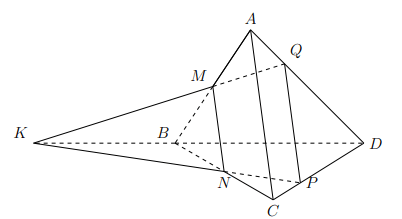
Vì \(QA \ne QD\) nên gọi \(K = QM ∩ BD\) suy ra \(KN ∩ CD = P\)
Theo định lý về giao tuyến ba mặt phẳng
Ta xét ba mặt phẳng (ABC) (ACD) và (MNQ).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}
{\left( {ABC} \right) \cap \left( {ACD} \right) = AC} \\
{\left( {ABC} \right) \cap \left( {MNQ} \right) = MN} \\
{\left( {ACD} \right) \cap \left( {MNQ} \right) = QP}
\end{array}} \right.\)
Vậy \(AC // MN\)nên \(AC // QP // NM\).
