Hai đường thẳng vuông góc
Góc của hai vectơ trong không gian
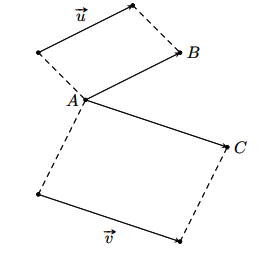
Trong không gian, cho 
\(\overrightarrow u ,\overrightarrow v\) là hai vectơ khác nhau và khác vectơ không. Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u ,\overrightarrow {AC} = \overrightarrow v\). Khi đó ta gọi \(\widehat {BAC},\left( {{0^0} \leqslant \widehat {BAC} \leqslant {{180}^0}} \right)\) là góc giữa hai vectơ \(\overrightarrow u\) và \(\overrightarrow v\), kí hiệu là \(\left( {\overrightarrow u ,\overrightarrow v } \right)\).
Hình vẽ minh họa
Ví dụ: Cho tứ diện đều ABCD có H là trung điểm của cạnh AB. Hãy tính góc giữa các cặp véc-tơ sau đây:
|
a) |
b) |
Hướng dẫn giải
Hình vẽ minh họa
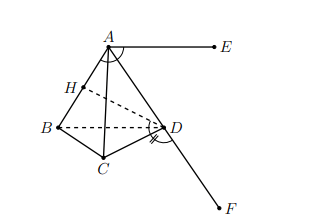
a) Dựng \(\overrightarrow {AE} = \overrightarrow {BD}\). Ta có:
\(\left( {\overrightarrow {AB} ,\overrightarrow {BD} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AE} } \right) = \widehat {BAE} = {120^0}\)
b) Dựng \(\overrightarrow {DF} = \overrightarrow {AD}\). Ta có:
\(\begin{matrix}
\left( {\overrightarrow {DH} ,\overrightarrow {AD} } \right) = \left( {\overrightarrow {DH} ,\overrightarrow {DF} } \right) = \widehat {HDF} \hfill \\
= {180^0} - {30^0} = {150^0} \hfill \\
\end{matrix}\)
Tích vô hướng của hai vectơ trong không gian
Trong không gian, cho \(\overrightarrow u ,\overrightarrow v\) là hai vectơ khác khác vectơ không. Tích vô hướng của hai vectơ \(\overrightarrow u\) và \(\overrightarrow v\) là một số, kí hiệu là \(\overrightarrow u .\overrightarrow v\), và được tính bởi công thức:
\(\overrightarrow u .\overrightarrow v = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.\cos \left( {\overrightarrow u ,\overrightarrow v } \right)\)
Chú ý: Trong trường hợp \(\overrightarrow u = 0\) hoặc \(\overrightarrow v = 0\) ta quy ước \(\overrightarrow u .\overrightarrow v = 0\)
II. Góc giữa hai đường thẳng trong không gian
Vectơ chỉ phương của đường thẳng
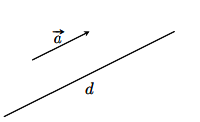
Vectơ \(\overrightarrow a\) khác vectơ không được gọi là vectơ chỉ phương của đường thẳng d nếu giá của vectơ \(\overrightarrow a\) song song hoặc trùng với đường thẳng d.
Hình vẽ minh họa
Nhận xét:
a) Nếu \(\overrightarrow a\) là vectơ chỉ phương của đường thẳng d thì vectơ \(k.\overrightarrow a\) với \(k \ne 0\) cũng là vectơ chỉ phương của d.
b) Một đường thẳng d trong không gian hoàn toàn được xác định nếu biết một điểm A thuộc d và một vectơ chỉ phương \(\overrightarrow a\) của nó.
c) Hai đường thẳng song song với nhau khi và chỉ khi chúng là hai đường thẳng phân biệt và có hai vectơ chỉ phương cùng phương.
Góc giữa hai đường thẳng trong không gian
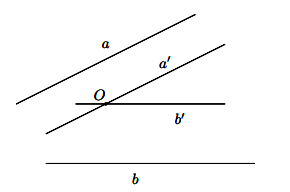
Góc giữa hai đường thẳng trong a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm và lần lượt song song với a và b.
Hình vẽ minh họa
Nhận xét
a) Để xác định góc giữa hai đường thẳng a và b ta có thể lấy điểm O thuộc một trong hai đường thẳng đó rồi vẽ một đường thẳng qua O và song song với đường thẳng còn lại.
b) Nếu \(\overrightarrow u\) là vectơ chỉ phương của đường thẳng a và \(\overrightarrow v\) là vectơ chỉ phương của đường thẳng b và \(\left( {\overrightarrow u ,\overrightarrow v } \right) = \alpha\) thì góc giữa hai đường thẳng a và b bằng \(\alpha\) nếu \({0^0} \leqslant \alpha \leqslant {90^0}\) và bằng \({180^0} - \alpha\) nếu \({90^0} \leqslant \alpha \leqslant {180^0}\).
c) Nếu a và b là hai đường thẳng song song hoặc trùng nhau thì góc giữa chúng bằng 00.
Ví dụ: Cho hình chóp S.ABC có \(SA = SB = SC = AB = AC = a\sqrt 2\) và BC = 2a. Tính góc giữa hai đường thẳng AC và SB.
Hình vẽ minh họa
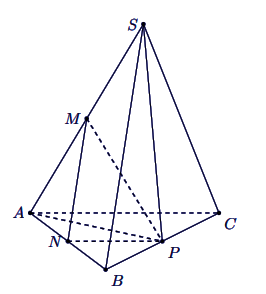
Cách 1:
Ta có SAB và SAC là tam giác đều, ABC và SBC là tam giác vuông cân cạnh huyền BC.
Gọi M, N, P lần lượt là trung điểm của SA, AB, BC, ta có MN // SB, NP // AC nên (AC, SB) = (NP, MN).
\(\begin{matrix}
MN = \dfrac{{AB}}{2} = \dfrac{{a\sqrt 2 }}{2} \hfill \\
NP = \dfrac{{AC}}{2} = \dfrac{{a\sqrt 2 }}{2} \hfill \\
AP = SP = \dfrac{{BC}}{2} = a \hfill \\
SA = a\sqrt 2 \hfill \\
\end{matrix}\)
Nên tam giác SAP vuông cân tại P => \(MP = \frac{{SA}}{2} = \frac{{a\sqrt 2 }}{2}\)
Vậy tam giác MNP đều
=> \(\left( {AC,SB} \right) = \left( {NP,NM} \right) = \widehat {MNP} = {60^0}\)
Cách 2:
\(\begin{matrix} \overrightarrow {AC} .\overrightarrow {SB} = (\overrightarrow {SC} - \overrightarrow {SA} ).\overrightarrow {SB} \hfill \\ = \overrightarrow {SC} .\overrightarrow {SB} - \overrightarrow {SA} .\overrightarrow {SB} \hfill \\ = 0 - SA.SB.\cos \widehat {ASB} \hfill \\ = - {a^2} \hfill \\ \cos (AC,SB) = \dfrac{{|\overrightarrow {AC} .\overrightarrow {SB} |}}{{AC.SB}} \hfill \\ \Rightarrow \cos (AC,SB) = \dfrac{{{a^2}}}{{a\sqrt 2 .a\sqrt 2 }} = \dfrac{1}{2} \hfill \\ \Rightarrow (AC,SB) = {60^0} \hfill \\ \end{matrix}\)
III. Hai đường thẳng vuông góc
Định nghĩa hai đường vuông góc
Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng 900.
Kí hiệu: a ⊥ b
Nhận xét
a) Nếu \(\overrightarrow u\) và \(\overrightarrow v\) lần lượt là các vectơ chỉ phương của hai đường thẳng a và b thì \(a \bot b \Leftrightarrow \overrightarrow u .\overrightarrow v = 0\).
b) Cho hai đường thẳng song song. Nếu một đường thẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
c) Hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau.
Ví dụ: Cho tứ diện ABCD có AB = AC = AD, \(\widehat {BAC} = \widehat {BAD} = {60^0}\). Gọi M và N lần lượt là trung điểm của AB và CD, chứng minh rằng MN là đường vuông góc chung của các đường thẳng AB và CD.
Hướng dẫn giải
Hình vẽ minh họa
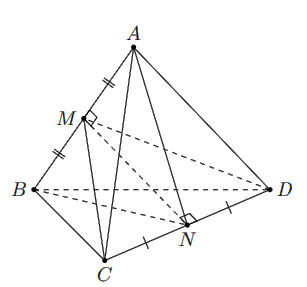
Từ giả thiết suy ra các tam giác ABC, ABD đều nên DM = CM, do đó ΔMCD cân tại M.
=> MN ⊥ CD
Mặt khác ΔBCD = ΔACD nên BN = AN
=> ΔNAB cân tại N
Từ đó suy ra NM ⊥ AB
Vậy MN là đường vuông góc chung của AB và CD.
