Hàm số lượng giác
1. Hàm số sin
Quy tắc đặt tương ứng với mỗi số thực 
\(x\) với số thực \(\sin x\)
\(\begin{matrix}
\sin x:\mathbb{R} \to \mathbb{R} \hfill \\
{\text{ }}x \mapsto y = \sin x \hfill \\
\end{matrix}\)
Được gọi là hàm số sin, kí hiệu là \(y= \sin x\). Tập xác định của hàm số là \(D=\mathbb{R}\).
2. Hàm số côsin
Quy tắc đặt tương ứng với mỗi số thực \(x\) với số thực \(\cos x\)
\(\begin{matrix} \cos x:\mathbb{R} \to \mathbb{R} \hfill \\ {\text{ }}x \mapsto y = \cos x \hfill \\ \end{matrix}\)
Được gọi là hàm số cosin, kí hiệu là \(y= \cos x\). Tập xác định của hàm số là \(D=\mathbb{R}\).
3. Hàm số tan
Hàm số tan là hàm số được xác định bởi công thức \(y = \frac{{\sin x}}{{\cos x}};\left( {\cos x \ne 0} \right)\), kí hiệu là \(y= \tan x\).
Tập xác định của hàm số \(y= \tan x\) là \(D=\mathbb{R}\backslash \left\{ \frac{\pi }{2}+k\pi ,k\in \mathbb{Z} \right\}\)
4. Hàm số cotan
Hàm số cotan là hàm số được xác định bởi công thức \(y = \frac{{\cos x}}{{\sin x}};\left( {\sin x \ne 0} \right)\), kí hiệu là \(y= \cot x\).
Tập xác định của hàm số \(y= \cot x\) là \(D=\mathbb{R}\backslash \left\{ k\pi ,k\in \mathbb{Z} \right\}\)
B. Tính tuần hoàn của hàm số lượng giác
Định nghĩa
Hàm số \(y=f(x)\) có tập xác định \(D\) được gọi là hàm số tuần hoán, nếu tồn tại một số \(T \ne 0\) sao cho với mọi \(x \in D\) ta có:
- \(x - T \in D\) và \(x + T \in D\)
- \(f(x+T)=f(x)\)
Số dương \(T\) nhỏ nhất thỏa mãn các tính chất trên được gọi là chu kì của hàm số tuần hoàn đó.
Người ta chứng minh được rằng:
- Hàm số \(y= \sin x\) tuần hoàn với chu kì \(T = 2\pi\)
- Hàm số \(y= \cos x\) tuần hoàn với chu kì \(T = 2\pi\)
- Hàm số \(y= \tan x\) tuần hoàn với chu kì \(T = \pi\)
- Hàm số \(y= \cot x\) tuần hoàn với chu kì \(T = \pi\)
Chú ý
- Hàm số \(y = \sin \left( {ax + b} \right)\) tuần hoàn với chu kì \(T = \frac{{2\pi }}{{\left| a \right|}}\)
- Hàm số \(y = \cos \left( {ax + b} \right)\) tuần hoàn với chu kì \(T = \frac{{2\pi }}{{\left| a \right|}}\)
- Hàm số \(y = \tan \left( {ax + b} \right)\) tuần hoàn với chu kì \(T = \frac{{\pi }}{{\left| a \right|}}\)
- Hàm số \(y = \cot \left( {ax + b} \right)\) tuần hoàn với chu kì \(T = \frac{{\pi }}{{\left| a \right|}}\)
Đặc biệt
a) Hàm số \(y = a\sin mx + b\cos nx + c,\left( {m,n \in \mathbb{Z}} \right)\) là hàm số tuần hoàn với chu kì \(T = \frac{{2\pi }}{{\left( {m,n} \right)}}\) với (m, n) là ước chung lớn nhất.
b) Hàm số \(y = a\tan mx + b\cot nx + c,\left( {m,n \in \mathbb{Z}} \right)\) là hàm số tuần hoàn với chu kì \(T = \frac{\pi }{{\left( {m,n} \right)}}\) với (m, n) là ước chung lớn nhất.
C. Sự biến thiên và đồ thị của hàm số lượng giác
1. Hàm số sin
- Tập xác định \(D=\mathbb{R}\) có nghĩa hàm số xác định với mọi \(x \in \mathbb{R}\)
- Tập giá trị \(T \in \left[ { - 1;1} \right]\) có nghĩa là \(- 1 \leqslant \sin x \leqslant 1\)
- Là hàm số tuần hoàn với chu kì \(2\pi\), có nghĩa là \(\sin \left( {x + k2\pi } \right) = \sin x,\left( {k \in \mathbb{Z}} \right)\)
- Hàm số nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\) và đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\)
- Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ \(O\) là tâm đối xứng.
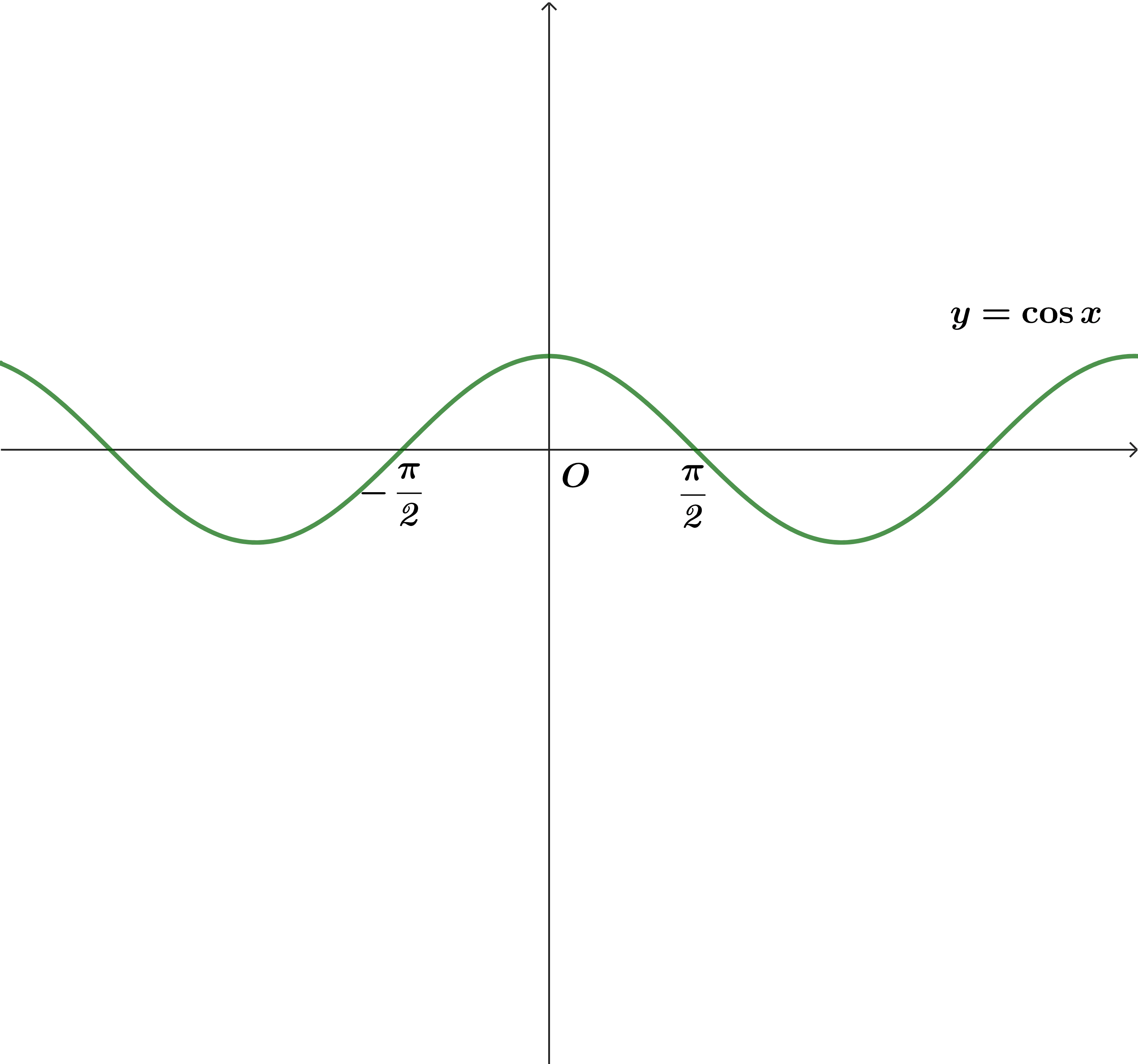
2. Hàm số côsin
- Tập xác định \(D=\mathbb{R}\) có nghĩa hàm số xác định với mọi \(x \in \mathbb{R}\)
- Tập giá trị \(T \in \left[ { - 1;1} \right]\) có nghĩa là \(- 1 \leqslant \cos x \leqslant 1\)
- Là hàm số tuần hoàn với chu kì \(2\pi\), có nghĩa là \(\cos \left( {x + k2\pi } \right) = \cos x,\left( {k \in \mathbb{Z}} \right)\)
- Hàm số nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi + k2\pi } \right)\) và đồng biến trên mỗi khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\)
- Là hàm số chẵn nên đồ thị hàm số nhận trục tung là trục đối xứng.
3. Hàm số tan
- Tập xác định \(D=\mathbb{R}\backslash \left\{ \frac{\pi }{2}+k\pi ,k\in \mathbb{Z} \right\}\)
- Tập giá trị \(T = \mathbb{R}\)
- Là hàm số tuần hoàn với chu kì \(\pi\), có nghĩa là \(\tan \left( {x + k\pi } \right) = \tan x,\left( {k \in \mathbb{Z}} \right)\)
- Hàm số đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\)
- Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ \(O\) là tâm đối xứng.
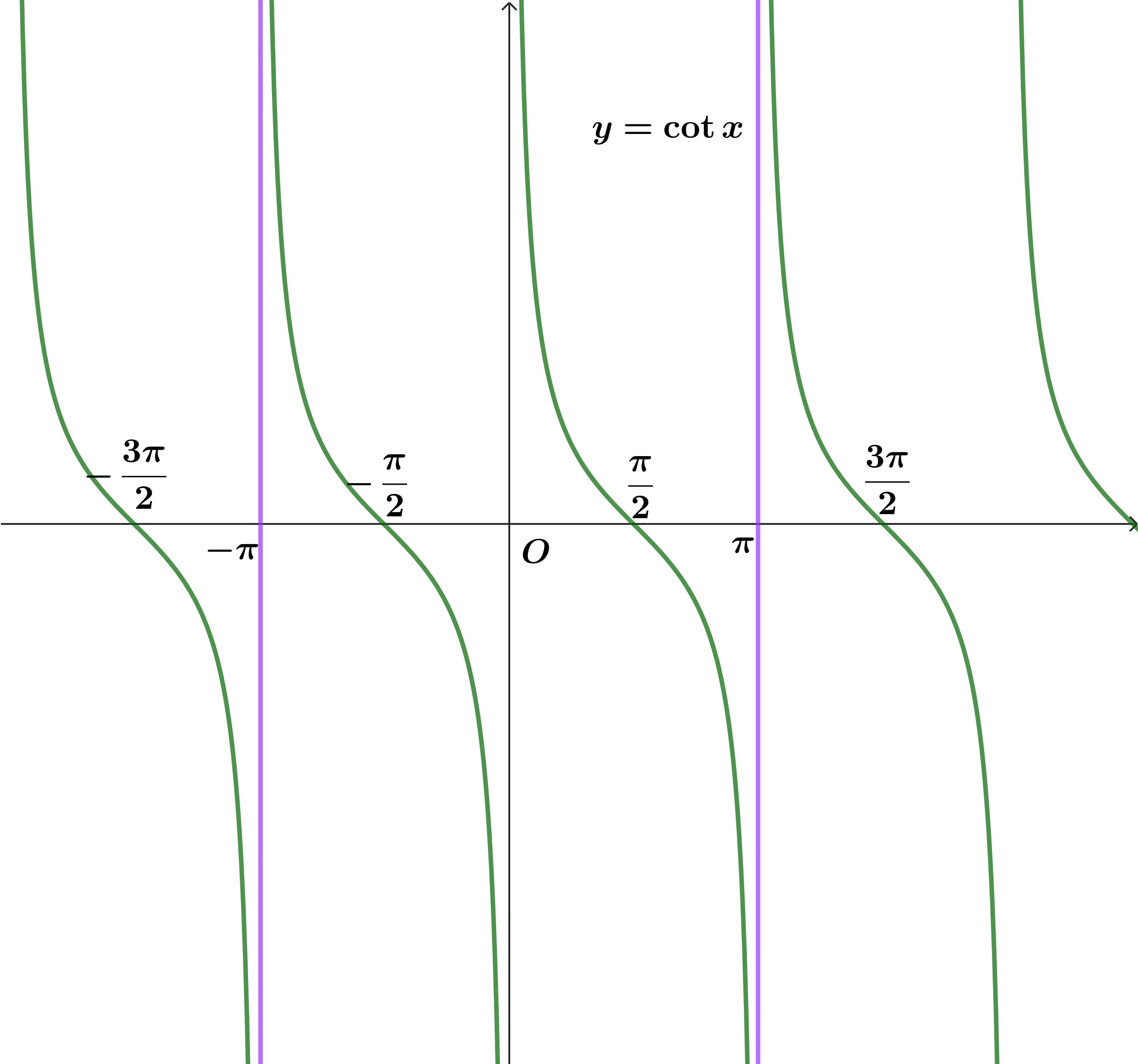
4. Hàm số cotan
- Tập xác định \(D=\mathbb{R}\backslash \left\{ k\pi ,k\in \mathbb{Z} \right\}\)
- Tập giá trị \(T = \mathbb{R}\)
- Là hàm số tuần hoàn với chu kì \(\pi\), có nghĩa là \(\cot \left( {x + k\pi } \right) = \cot x,\left( {k \in \mathbb{Z}} \right)\)
- Hàm số đồng biến trên mỗi khoảng \(\left( { k\pi ;\pi + k\pi } \right)\)
- Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ \(O\) là tâm đối xứng.
