Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

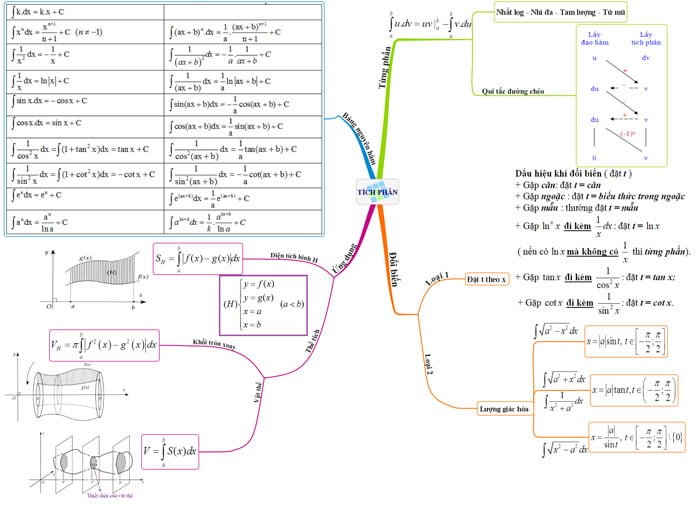
Công thức tích phân

Định nghĩa, tính chất và bài tập minh họa

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Trong chương trình Toán 12, tích phân là một nội dung quan trọng, thường xuyên xuất hiện trong các bài kiểm tra định kỳ cũng như đề thi tốt nghiệp THPT. Để giải nhanh và chính xác các bài toán liên quan, việc nắm vững công thức tích phân là yêu cầu bắt buộc đối với học sinh lớp 12.

Bài viết Công thức tích phân – Định nghĩa, tính chất và bài tập minh họa sẽ giúp bạn hệ thống hóa toàn bộ các công thức tích phân Toán 12 từ cơ bản đến nâng cao, kèm theo cách vận dụng linh hoạt trong từng dạng toán thường gặp. Thông qua đó, học sinh không chỉ hiểu bản chất của tích phân mà còn rèn luyện kỹ năng giải bài tập một cách hiệu quả, tránh nhầm lẫn khi áp dụng công thức.

CÔNG THỨC TÍCH PHÂN

Định nghĩa tích phân
Tính chất của tích phân – Công thức tích phân
Một số phương pháp tính tích phân
Bài tập minh họa áp dụng công thức tích phân

Định nghĩa tích phân

Cho hàm f(x) liên tục trên khoảng K và a, b là hai số bất kỳ thuộc K. Nếu F(x) là một nguyên hàm của f(x) thì hiệu số F(b) − F(a) được gọi là tích phân của f(x) từ a đến b và ký hiệu là $\int\limits_a^b {f\left( x \right)dx}$ .

Tính chất của tích phân – Công thức tích phân

Cho các hàm số f(x), g(x) liên tục trên K và a, b, c là ba số thuộc K.

$\int\limits_a^b {f\left( x \right)dx} = 0$

$\int\limits_a^b {f\left( x \right)dx} = - \int\limits_b^a {f\left( x \right)dx}$

$\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx}$

$\int\limits_a^b {k.f\left( x \right)dx} = k\int\limits_a^b {f\left( x \right)dx}$

$\int\limits_a^b {\left[ {f\left( x \right) \pm g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx} \pm \int\limits_a^b {g\left( x \right)dx}$

Một số phương pháp tính tích phân

Phương pháp đổi biến số

Công thức đổi biến số $\int\limits_a^b {f\left[ {u\left( x \right)} \right]u'\left( x \right)dx} = \int\limits_{u\left( a \right)}^{u\left( b \right)} {f\left( u \right)du}$ . Trong đó f(x) là hàm số liên tục và u(x) có đạo hàm liên tục trên khoảng J sao cho hàm hợp xác định trên J; a, b ∈ J.

Các phương pháp đổi biến số thường gặp:

Cách 1: Đặt u = u(x) (u là một hàm theo x).

Cách 2: Đặt x = x(t) (x là một hàm theo t).

Phương pháp tích phân từng phần

Định lí:

Nếu u(x), v(x) là hai hàm số có đạo hàm liên tục trên khoảng K và a, b là hai số thuộc K thì $\int\limits_a^b {u\left( x \right)v'\left( x \right)dx} = \left. {u\left( x \right)v\left( x \right)} \right|_a^b - \int\limits_a^b {v\left( x \right)u'\left( x \right)dx}$ .

Bài tập minh họa áp dụng công thức tích phân

Ví dụ 1: Áp dụng công thức tính tích phân cơ bản, tính các tích phân sau:

a) $I = \int_1^2 {\frac{{{x^2} - 2x}}{{{x^2}}}dx}$ b) $I = \int_0^{\frac{\pi }{4}} {{{\cos }^2}xdx}$

Hướng dẫn giải

a) Ta có:

$I = \int_1^2 {\frac{{{x^2} - 2x}}{{{x^2}}}dx} = \int_1^2 {\left( {\frac{1}{x} - \frac{2}{{{x^2}}}} \right)dx} = \left. {\left( {\ln |x| + \frac{2}{x}} \right)} \right|_1^2$

$= \left( {\ln 2 + 1} \right) - \left( {\ln 1 + 2} \right) = - 1 + \ln 2$

b) Ta có:

$I = \int_0^{\frac{\pi }{4}} {{{\cos }^2}xdx} = \int_0^{\frac{\pi }{4}} {\left( {1 + \cos 2x} \right)dx} = \left. {\frac{1}{2}\left( {x + \frac{1}{2}\sin 2x} \right)} \right|_0^{\frac{\pi }{4}}$ $= \frac{{\pi + 2}}{8}$

Ví dụ 2. Áp dụng phương pháp đổi biến số, ta tính các tích phân sau:

a) $I = \int_0^3 {\frac{x}{{1 + x\sqrt {1 + x} }}dx}$ b) $I = \int_0^3 {{x^3}\sqrt {{x^2} + 1} dx}$ c) $I = \int_0^1 {\frac{{dx}}{{\sqrt {4 - {x^2}} }}}$

Hướng dẫn giải

a) Đặt $t = \sqrt {1 + x} \Rightarrow {t^2} = 1 + x \Rightarrow 2dt = dx$

Đổi cận $\left\{ \begin{gathered} x = 0 \Rightarrow t = 1 \hfill \\ x = 3 \Rightarrow t = 2 \hfill \\ \end{gathered} \right.$

Khi đó ta có:

$I = \int_0^3 {\frac{x}{{1 + x\sqrt {1 + x} }}dx} = \int_0^2 {\frac{{{t^2} - 1}}{{t + 1}}.2tdt}$

$= \int_0^2 {2t\left( {t - 1} \right)dt}$ $= \left. {\left( {\frac{2}{3}{t^3} - {t^2}} \right)} \right|_1^2 = \frac{5}{3}$

b) Đặt $t = \sqrt {{x^2} + 1} \Rightarrow \left\{ \begin{gathered} {x^2} = {t^2} - 1 \hfill \\ xdx = tdt \hfill \\ \end{gathered} \right.$

Đổi cận $\left\{ \begin{gathered} x = 0 \hfill \\ x = 2 \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} t = 1 \hfill \\ t = \sqrt 5 \hfill \\ \end{gathered} \right.$

Khi đó ta có:

$I = \int_1^{\sqrt 5 } {\left( {{t^2} - 1} \right).t.tdt} = \left. {\left( {\frac{{{t^5}}}{5} - \frac{{{t^2}}}{3}} \right)} \right|_1^{\sqrt 5 } = \frac{2}{{15}} + \frac{{10\sqrt 5 }}{3}$

c) Đặt $x = \sin 2t;t \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right] \Rightarrow dx = 2\cos tdt$

Đổi cận $x = 0 \Rightarrow t = 0;x = 1 \Rightarrow t = \frac{\pi }{6}$

Khi đó ta có:

$I = \int_0^1 {\frac{{dx}}{{\sqrt {4 - {x^2}} }}} = \int_0^{\frac{\pi }{6}} {\frac{{2\cos tdt}}{{\sqrt {4 - 4{{\sin }^2}t} }}}$ $= \int_0^{\frac{\pi }{6}} {dt} = \left. t \right|_0^{\frac{\pi }{6}} = \frac{\pi }{6}$ .

Ví dụ 3. Vận dụng phương pháp tính tích phân từng phần, tính các tích phân sau:

a) $I = \int_0^1 {x.{e^{2x}}dx}$ b) $I = \int_1^2 {\left( {{x^2} - 1} \right)\ln xdx}$

Hướng dẫn giải

a) Đặt $\left\{ \begin{gathered} u = x \hfill \\ dv = {e^{2x}}.dx \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} du = dx \hfill \\ v = \frac{{{e^{2x}}}}{2} \hfill \\ \end{gathered} \right.$

Khí đó ta có:

$I = \left. {\frac{{x{e^{2x}}}}{2}} \right|_0^1 - \int_0^1 {\frac{{{e^{2x}}}}{2}dx} = \frac{{{e^2}}}{2} - \left. {\frac{{{e^{2x}}}}{4}} \right|_0^1 = \frac{{{e^2} + 1}}{4}$

b) Đặt $\left\{ \begin{gathered} u = \ln x \hfill \\ dv = \left( {{x^2} - 1} \right).dx \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} du = dx \hfill \\ v = \frac{{{x^3} - 3x}}{3} \hfill \\ \end{gathered} \right.$

Khi đó ta có:

$I = \left. {\frac{{\left( {{x^3} - 3x} \right)\ln x}}{3}} \right|_1^2 - \int_1^2 {\frac{{{x^2} - 3}}{3}dx }$

$= \frac{{2\ln 2}}{3} - \left. {\left( {\frac{{{x^3}}}{9} - x} \right)} \right|_1^2 = \frac{{2\ln 2}}{3} + \frac{2}{9}$

Các tài liệu liên quan:

---------------------------------------------------------------

Có thể thấy rằng, công thức tích phân đóng vai trò then chốt trong việc giải các bài toán tích phân và ứng dụng của tích phân trong Toán 12. Việc ghi nhớ đúng công thức, hiểu rõ định nghĩa và nắm vững các tính chất sẽ giúp học sinh xử lý bài toán nhanh hơn, chính xác hơn trong các kỳ thi quan trọng.

Hy vọng bài viết Công thức tích phân – Định nghĩa, tính chất và bài tập minh họa đã mang đến cho bạn một cái nhìn hệ thống và dễ tiếp cận về chuyên đề tích phân lớp 12. Đừng quên luyện tập thêm nhiều bài tập áp dụng để biến công thức thành kỹ năng, từ đó tự tin chinh phục các dạng toán tích phân trong chương trình và đề thi THPT Quốc gia.

Tải về

Chọn file muốn tải về:

Công thức tích phân

414,7 KB

Tải file định dạng .DOC
253 KB

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

30 lượt tải tài liệu

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Chia sẻ bởi:
Đen2017

731

Bài trước

Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!