Đề thi thử Toán vào lớp 10 lần 3 phòng GD&ĐT Thái Hòa, Nghệ An năm 2024 - 2025
Đề thi tuyển sinh lớp 10 môn Toán có đáp án
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ VÀO LỚP 10 THPT NĂM HỌC
2024 - 2025 (Lần 3)
THỊ XÃ THÁI HÒA
Môn thi: TOÁN
Thời gian làm bài: 120 phút
Câu 1 (2,5 điểm)
1) Tính giá trị của biểu thức
( )
2
32 3 2 2 8.A = + − −
2) Rút gọn biểu thức
12
:
16
44
xx
B
x
xx
+
=+
−
−−
với
0x
và
16.x
3) Tìm các giá trị của
m
để hai đường thẳng
2
2y x m=+
và
( )
1 2 3y m x m= − + +
( )
1m
cắt
nhau tại một điểm trên trục tung.
Câu 2 (2,0 điểm)
1) Giải phương trình
2
4 1 0.xx− − =
2) Cho phương trình
2
4 2 0xx− + =
có hai nghiệm dương
1
,x
2
x
thoả mãn
12
.xx
Không giải
phương trình, hãy tính giá trị của biểu thức
22
12
11
2024.P
xx
= − +
Câu 3 (2,0 điểm)
1) Một phòng họp có
320
ghế ngồi (loại ghế một chỗ ngồi) được xếp thành nhiều hàng ghế và
số lượng ghế ở mỗi hàng là như nhau. Người ta tổ chức một buổi hội thảo dành cho
429
người tại
phòng họp đó nên phải xếp thêm
1
hàng ghế và mỗi hàng ghế phải xếp nhiều hơn số lượng ban
đầu
3
ghế. Hỏi lúc đầu phòng họp đó có bao nhiêu hàng ghế.
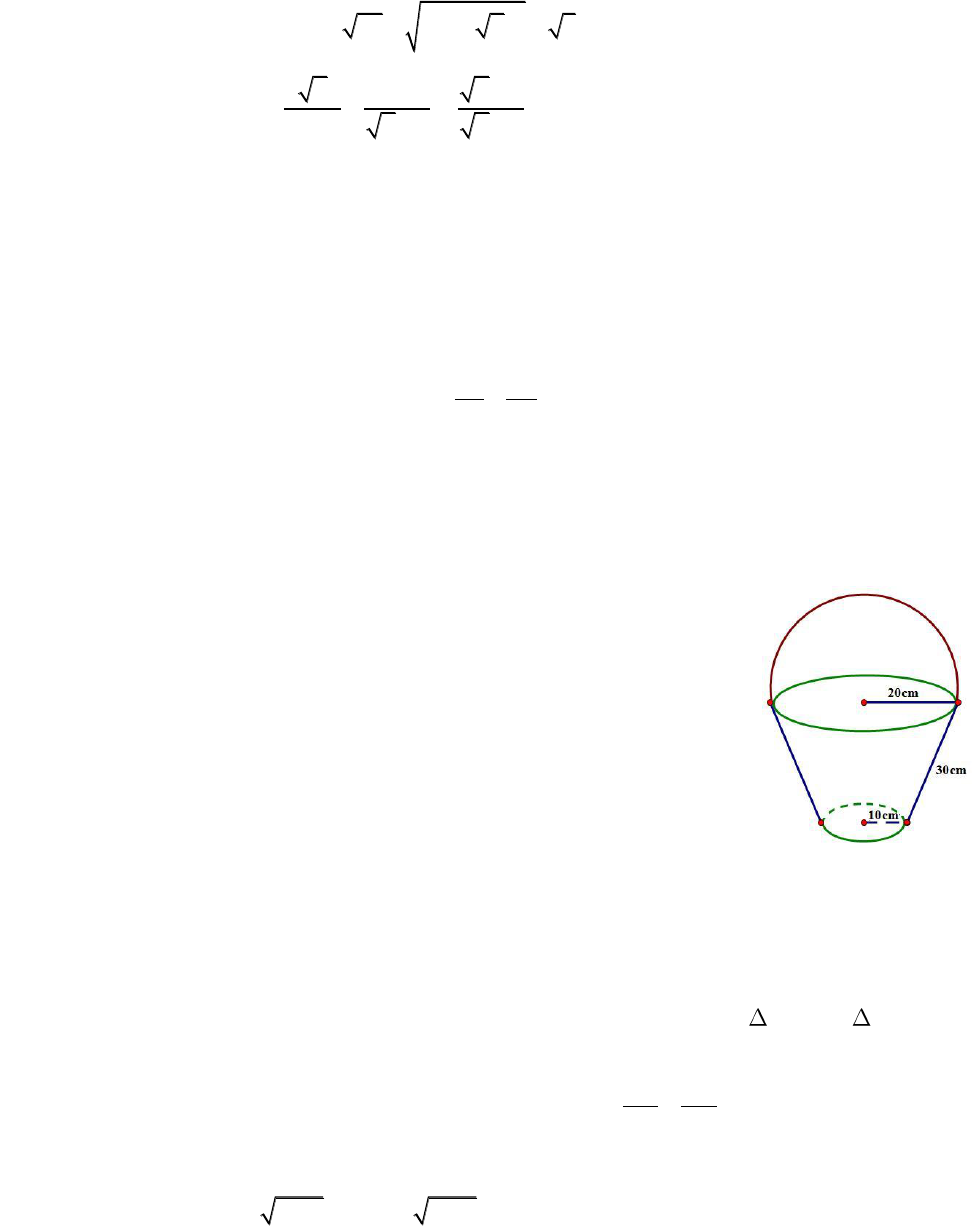
2) Người ta muốn làm một cái xô đựng nước có dạng hình nón cụt, có
các kích thước cho ở hình vẽ bên, hãy tính diện tích tôn cần dùng để làm cái
xô đó (cho biết phần mép nối không đáng kể và lấy
3,14
).
Câu 4 (3,0 điểm)
Cho đường tròn
( )
;OR
có hai đường kính
AB
và
CD
vuông góc với
nhau. Trên cung nhỏ
AC
lấy điểm
M
bất kì (
M
khác
A
và
C
),
BM
cắt
OC
tại điểm
E
và
DM
cắt
OA
tại điểm
.F
a) Chứng minh
OFMC
là tứ giác nội tiếp.
b) Gọi
K
là giao điểm của hai đường thẳng
CM
và
.AB
Chứng minh
CMF EMA∽
và
. . .KF OA AF KB=
c) Xác định vị trí của điểm
M
trên cung nhỏ
AC
để tổng
OA OC
AF CE
+
đạt giá trị nhỏ nhất.
Câu 5 (0,5 điểm)
Giải phương trình
( ) ( )
2
1 2 6 7 7 12.x x x x x x+ + + + + = + +
--- HẾT ---
Họ và tên thí sinh: ................................................. SBD:............................
HƯỚNG DẪN CHẤM THI THỬ LỚP 10 LẦN 3 NĂM HỌC 2024 - 2025
MÔN THI: TOÁN
(Hướng dẫn chấm này có 04 trang)
Câu
ý
Nội dung
Điểm
Câu 1
(2,5
điểm)
1)
Tính giá trị của biểu thức
( )
2
32 3 2 2 8.A = + − −
1,0
4 2 3 2 2 2 2A = + − −
(lưu ý: HS tính được từng căn cho 0,25 điểm)
0,75
3.=
0,25
2)
Rút gọn biểu thức
12
:
16
44
xx
B
x
xx
+
=+
−
−−
với
0x
và
16.x
1,0
( )( ) ( )( )
42
:
4
4 4 4 4
x x x
B
x
x x x x
++
=+
−
+ − + −
0,25
( )( )
2 4 4
.
2
44
xx
x
xx
+−
=
+
−+
0,25
( )
( )( )
22
4
.
2
44
x
x
x
xx
+
−
=
+
−+
0,25
2
.
4x
=
+
0,25
3)
Tìm các giá trị của
m
để hai đường thẳng
2
2y x m=+
và
( )
1 2 3y m x m= − + +
( )
1m
cắt nhau tại một điểm trên trục tung.
0,5
Hai đường thẳng
2
2y x m=+
và
( )
1 2 3y m x m= − + +
( )
1m
cắt nhau tại một
điểm trên trục tung
2
21
'
'
23
m
aa
bb
mm
−
=
=+
0,25
2
3
3
1
1
2 3 0
3
m
m
m
m
mm
m
= −
=−
− − =
=
(thoả mãn điều kiện
1m
).
Vậy hai đường thẳng
2
2y x m=+
và
( )
1 2 3y m x m= − + +
( )
1m
cắt nhau tại
một điểm trên trục tung khi
1.m =−
0,25
Câu 2
(2,0
điểm)
1)
Giải phương trình
2
4 1 0.xx− − =
1,0
Phương trình
2
4 1 0xx− − =
có
1,a =
' 2,b =−
1c =−
0,25
nên
( ) ( )
2
' 2 1. 1 5 0. = − − − =
0,25
Do đó phương trình có hai nghiệm phân biệt là
1
25
25
1
x
+
= = +
0,25
và
1
25
2 5.
1
x
−
= = −
0,25
2)
Cho phương trình
2
4 2 0xx− + =
có hai nghiệm dương
1
,x
2
x
thoả mãn
12
.xx
Không giải phương trình, hãy tính giá trị của biểu thức
22
12
11
2024.P
xx
= − +
1,0
Vì phương trình có hai nghiệm
1
,x
2
x
nên theo hệ thức Vi-ét ta có
12
12
4
.
.2
xx
xx
+=
=
0,25
Ta có
( )
( )( )
( )
22
1 2 1 2
21
22
22
12
1 2 1 2
11
2024 2024 2024
..
x x x x
xx
P
xx
x x x x
− + −
−
= − + = + = +
0,25
( )
2
12
2
4
2024
2
xx−−
=+
0,25
( )
2
2
1 2 1 2
4 4 .
4 4.2
2024 2024 2024 2 2.
41
x x x x− + −
−−
= + = + = −
0,25
Câu 3
(2,0
điểm)
1)
Một phòng họp có
320
ghế ngồi (loại ghế một chỗ ngồi) được xếp thành
nhiều hàng ghế và số lượng ghế ở mỗi hàng là như nhau. Người ta tổ chức
một buổi hội thảo dành cho
429
người tại phòng họp đó nên phải xếp thêm
1
hàng ghế và mỗi hàng ghế phải xếp nhiều hơn số lượng ban đầu
3
ghế.
Hỏi lúc đầu phòng họp đó có bao nhiêu hàng ghế.
1,5
Gọi số hàng ghế lúc đầu của phòng họp là
x
( đơn vị: hàng, điều kiện:
*
x
)
0,25
Ta có số hàng ghế sau khi xếp thêm của phòng họp là
1x +
(hàng).
0,25
Số ghế trong mỗi hàng lúc đầu là
320
x
(ghế).
Số ghế trong mỗi hàng sau khi xếp thêm là
429
1x +
(ghế).
0,25
Vì mỗi hàng ghế phải xếp nhiều hơn số lượng ban đầu
3
ghế nên ta có
phương trình
429 320
3.
1xx
−=
+
0,25
Khử mẫu và biến đổi ta được
2
429 320 320 3 3x x x x− − = +
2
3 106 320 0.xx − + =
0,25
Giải phương trình ta được
1
10
3
x =
(không thỏa mãn),
2
32x =
(thỏa
mãn).
Vậy lúc đầu phòng họp đó có
32
hàng ghế.
0,25
2)
Người ta muốn làm một cái xô đựng nước có dạng
hình nón cụt, có các kích thước cho ở hình vẽ bên,
hãy tính diện tích tôn cần dùng để làm cái xô đó (cho
biết phần mép nối không đáng kể và lấy
3,14
).
0,5
Diện tích tôn cần dùng để làm cái xô đó bằng tổng diện tích xung quanh của hình
nón cụt và diện tích của hình tròn đáy có bán kính
10cm.
0,25
Đề thi thử tuyển sinh vào lớp 10 môn Toán phòng GD&ĐT Thái Hòa, Nghệ An năm 2024 - 2025
VnDoc.com xin gửi tới các bạn Đề thi thử Toán vào lớp 10 lần 3 phòng GD&ĐT Thái Hòa, Nghệ An năm 2024 - 2025 để bạn đọc cùng tham khảo. Đây là tài liệu hay cho các bạn ôn luyện, chuẩn bị cho kì thi tuyển sinh vào lớp 10 sắp tới. Đề thi có đáp án đi kèm cho các bạn so sánh đối chiếu sau khi làm xong. Mời các bạn cùng tham khảo chi tiết và tải về bài viết dưới đây.
