VnDoc.com

Đề thi thử Toán vào lớp 10 phòng GD&ĐT TP Nam Định năm 2024 - 2025

Đề thi tuyển sinh lớp 10 môn Toán có đáp án

UBND THÀNH PHỐ NAM ĐỊNH

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO

ĐỀ THI THỬ TUYỂN SINH LỚP 10 THPT

NĂM HỌC 2024 - 2025

Môn: TOÁN – Lớp 9

(Đề thi gồm 02 trang)

Thời gian làm bài 120 phút

Phần I: Trắc nghiệm khách quan (2,0 điểm)

Chọn chữ cái đứng trước câu trả lời đúng và ghi vào tờ giấy làm bài.

Câu 1. Điều kiện xác định của biểu thức

1

2

x



là

A.

2.

x



B.

2.

x



C.

2.

x



D.

2.

x



Câu 2. Rút gọn biểu thức

 

2

1

a a

 

với

0

a



được kết quả bằng

Câu 3: Khi đồ thị hàm số

1

y x m

  

cắt trục hoành tạo điểm có hoành độ

2

x



thì giá trị

của tham số

m

bằng

Câu 4. Biết phương trình

2

2 1 0

x x

  

có hai nghiệm

1 2

;

x x

. Giá trị của biểu thức

2 2

1 2

x x



bằng

Câu 5. Một hình chữ nhật có chiều dài gấp đôi chiều rộng. Nếu giảm chiều dài

5

m

và tăng

chiều rộng

5

m

thì được một hình vuông. Chu vi của hình chữ nhật ban đầu là

Câu 6. Cho hai đường tròn





;3

O cm

và





';5

O cm

có đoạn nối tâm

' 7

OO cm



. Vị trí tương

đối của hai đường tròn là

A.

c

ắt nhau.

B.

ti

ếp xúc trong.

C.

không giao nhau.

D.

ti

ếp xúc

ngo

ài

.

Câu 7. Cho đường tròn





;1

O cm

. Từ điểm A nằm ngoài đường tròn





;1

O cm

sao cho

2

OA cm



kẻ hai tiếp tuyến

,

AB AC

đến đường tròn (





, ;1

B C O cm

 ). Độ dài cung

BC

lớn bằng

A.

2

.

3

cm

B.

2

.

3

cm



C.

4

.

3

cm



D.

4

.

3

cm

Câu 8. Quay tam giác

ABC

vuông tại

A

có

10 ; 6

BC cm AC cm

 

quanh cạnh

AB

cố định

được hình nón. Thể tích của hình nón đó bằng

A.

3

96 .

cm



B.

3

128 .

cm



C.

3

200 .

cm



D.

3

218 .

cm



Phần II. Tự luận (8,0 điểm)

Bài 1. (1,5 điểm)

1) Rút gọn biểu thức





3 3

12 4 2 3 1

3 1

 



  

 



 

.

2) Cho biểu thức

3 3 5 12

:

16

4 4

x x x

P

x

x x

 

  

 

 



 

 

với

0; 16

x x

 

. Chứng minh

1

P



với

mọi giá trị của x thuộc điều kiện xác định.

Bài 2. (1,0 điểm) Giải hệ phương trình

    

2 2

5

1 1 1 0.

x y

x x x y



 





    





A.

1 2

a



.

B.

1

.

C.

1

a



.

D.

2 1

a



.

A.

1.

m



B.

3.

m



C.

2.

m



D.

1.

m

 

A.

4.

B.

2.



C.

6

.

D.

2.

A.

30 .

m

B.

45 .

m

C.

50 .

m

D.

60 .

m

Bài 3. (1,5 điểm) Cho phương trình

2 2

2 1 0

x x m

   

(m là tham số).

a) Giải phương trình với

1.

m



b) Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt

1 2

,

x x

thoả mãn

1 2

2 1

1 1

1

x x

 

 

.

Bài 4. (3,0 điểm)

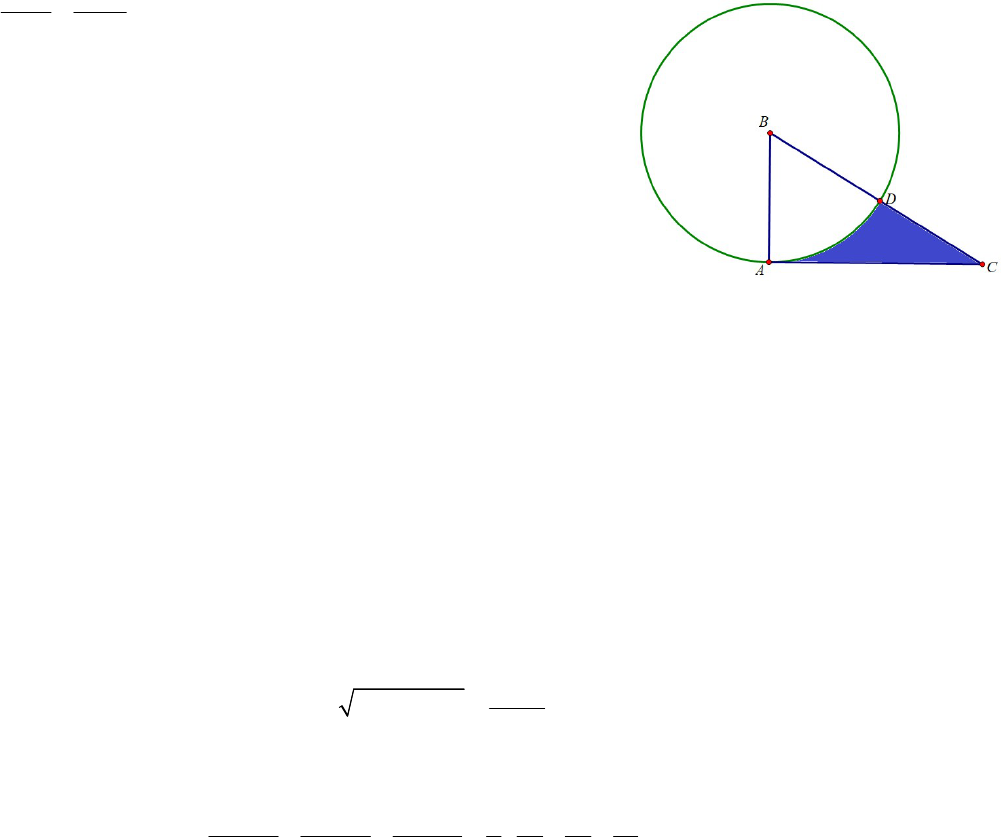
1) Cho tam giác

ABC

vuông tại A. Biết



0

3 ; 30

AC cm ACB  . Vẽ đường tròn tâm B bán kính

BA

cắt cạnh

BC

tại

D

. Tính diện tích phần mặt phẳng tô đậm ở

hình vẽ bên. (Kết quả làm tròn đến chữ số thập phân thứ

hai).

2) Cho tam giác ABC nhọn

( )

AB AC



. Đường tròn

( ; )

O R

đường kính

BC

cắt các cạnh

;

AB AC

lần lượt tại

,

E D

. Các đường thẳng

BD

và

CE

cắt nhau tại

I

. Đường thẳng AI cắt

BC

tại

H

.

a) Chứng minh tứ giác

BHIE

và

CDIH

là các tứ giác nội tiếp.

b) Đường thẳng

DH

cắt đường thẳng

CE

tại

M

và cắt đường tròn

( ; )

O R

tại điểm thứ

hai là N (N khác

D

). Chứng minh

/ /

NE AI

và

. .

IE CM IM CE



.

Bài 5. (1,0 điểm)

1) Giải phương trình

2

6 1

4 2 6 1

x

x x x

x



   

.

2) Cho

, ,

x y z

là các số dương.

Chứng minh

2 2 2

1 1 1 1 1 1 1

2

x yz y zx z xy xy yz zx

 

    

 

  

 

.

-------HẾT-------

Họ và tên thí sinh:……………………………. Giám thị 1:…………………………………….

SBD:……………………………………………. Giám thị 2: …………………………………….

UBND THÀNH PHỐ NAM ĐỊNH

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO

HƯỚNG DẪN CHẤM

ĐỀ THI THỬ TUYỂN SINH LỚP 10 THPT

Môn: Toán 9

(Hư

ớng dẫn chấm gồm 04 trang)

I. Phần I: Trắc nghiệm khách quan: (2,0 điểm) Mỗi ý đúng được 0,25 điểm

Câu 1

Câu 2

Câu 3

Câu 4

Câu 5

Câu 6

Câu 7

Câu 8

C

A

B

C

D

A

C

A

II. Phần II. Tự luận: (8.0 điểm)

Bài 1.

Câu Nội dung Điểm

1)

1,0 điểm

Ta có





 





2

3 3 1

3 3

12 4 2 3 1 2 3 3 1 1

3 1 3 1

 



 



 

      

 

 

 

0,25

















2 3 3 1 3 1 3 1 3 1 3 1 2

        

Kết luận:….

0,25

2)

1,0 điểm

b)Với

0; 16

x x

 

ta có

  

3 3 5 12 3 3 5 12

: :

16

4 4 4 4

4 4

x x x x x x

P

x

x x x x

x x

 

     

 

   

 



   

 

 

0,25









     

3 4 5 12

3 3 4

: :

4 4

4 4 4 4

x x x

x x x x

x x

x x x x

   

  

 

 

   

0,25









 

4 4

3 3

.

4

x x

 

 

 





0,25

Vì

0; 16

x x

 

nên

3

1 1

x

 

.

K

ết luận:….

0,25

Bài 2:

Câu Nội dung Điểm

3)

1,0 điểm





      

2 2

5 1

1 1 1 0 2

x y

x x x y



 





    





Biến đổi phương trình (2) ta được









1 1 0

x x y

   

0,25

Trường hợp 1:

1 0 1

x x

   

. Thay vào phương trình (1), tìm

được

2

y

 

0,25

Trường hợp 2:

1 0 1

x y x y

     

. Thay vào phương trình (2),

rút gọn ta được

2

2 0

y y

  

.

Giải phương trình tìm được

1; 2

y y

  

0,25

+)

1 2

y x

  

+)

2 1

y x

    

0,25

Đề thi thử vào 10 môn Toán phòng GD&ĐT Thành phố Nam Định năm 2024 - 2025

VnDoc.com xin gửi tới các bạn Đề thi thử vào lớp 10 môn Toán phòng GD&ĐT Thành phố Nam Định năm 2024 - 2025 để bạn đọc cùng tham khảo. Đây là tài liệu hay cho các bạn ôn luyện, chuẩn bị cho kì thi tuyển sinh vào lớp 10 sắp tới. Đề thi có đáp án đi kèm cho các bạn so sánh đối chiếu sau khi làm xong. Mời các bạn cùng tham khảo chi tiết và tải về bài viết dưới đây.