Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 10 Khóa học Lớp 10 Toán 10 - Cánh diều
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Đề thi học kì 1 Toán 10 Cánh Diều Đề 3

Mô tả thêm:

Mời các bạn học cùng thử sức với Đề thi học kì 1 môn Toán lớp 10 theo chương trình sách Cánh Diều nha!
  • Thời gian làm: 90 phút
  • Số câu hỏi: 45 câu
  • Số điểm tối đa: 45 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Bắt đầu làm bài
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
  • Câu 1: Vận dụng

    Chọn khẳng định đúng

    Cho hàm số y = ax2 + bx + c có đồ thị như hình dưới đây. Khẳng định nào sau đây là đúng?

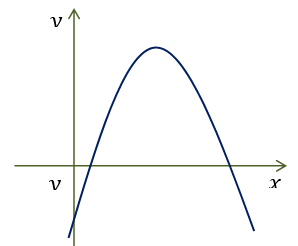
    Nhìn vào đồ thị ta có:

    Bề lõm hướng xuống  ⇒ a < 0.

    Hoành độ đỉnh x = - \frac{b}{2a} > 0\Rightarrow \frac{b}{2a} < 0 \Rightarrow b > 0 .

    Đồ thị hàm số cắt trục tung tại điểm có tung độ âm  ⇒ c < 0.

    Do đó: a < 0, b > 0, c < 0.

  • Câu 2: Vận dụng cao

    Tính độ dài vectơ

    Cho hình thang vuông ABCD có \widehat{A} = \widehat{D} = 90^{0}. Tính độ dài vectơ \overrightarrow{\alpha} = \overrightarrow{DA} + \overrightarrow{DB} + \overrightarrow{DC}, biết AB = AD = 2,CD = 4.

    Hình vẽ minh họa

    Dựng hình bình hành ADBM ta có: \overrightarrow{DA} + \overrightarrow{DB} = \overrightarrow{DM}

    Do BM//DA nên BM\bot DC tại H,

    Tứ giác ADBH là hình vuông nên BH = 2, ta cũng tính được MH = 4.

    Dựng hình bình hành DMNC ta có: \overrightarrow{DA} + \overrightarrow{DB} + \overrightarrow{DC} = \overrightarrow{DN}.

    Gọi K là hình chiếu vuông góc của N lên DC. Ta chứng minh được HMNK là hình vuông.

    \Rightarrow HK = NK = 4,DK = 6

    Ta có: DN = \sqrt{DK^{2} + KN^{2}} = 2\sqrt{13}

  • Câu 3: Thông hiểu

    Tìm tọa độ điểm không thuộc miền nghiệm của bất phương trình

    Miền nghiệm của bất phương trình x+2(y+1)-4y\leq 2(x+1)-5y không chứa điểm có tọa độ:

    Ta có: 

    x+2(y+1)-4y\leq 2(x+1)-5y

    \begin{matrix} \Rightarrow x + 2y + 2 - 4y \leqslant 2x + 2 - 5y \hfill \\ \Rightarrow - x + 3y \leqslant 0 \hfill \\ \end{matrix}

    Thay x=3;y=2 vào bất phương trình ta được: - 3 + 3.2= 5 > 0

    Vậy (3;2) không thuộc miền nghiệm của bất phương trình.

  • Câu 4: Nhận biết

    Tìm điểm thỏa mãn

    Cho hệ bất phương trình \left\{ \begin{matrix} x + y - 2 \leq 0 \\ 2x - 3y + 2 > 0 \\ \end{matrix} ight.. Trong các điểm sau, điểm nào không thuộc miền nghiệm của hệ bất phương trình?

    Thay lần lượt tọa độ các điểm vào hệ bất phương trình. Ta thấy chỉ có điểm N( - 1;1) thỏa mãn cả hai phương trình trong hệ \left\{ \begin{matrix} x + y - 2 \leq 0 \\ 2x - 3y + 2 > 0 \\ \end{matrix} ight..

  • Câu 5: Thông hiểu

    Chọn khẳng định đúng

    Cho hệ bất phương trình \left\{ \begin{matrix} y - x > 3 \\ - 1 - x + y < 0 \\ \end{matrix} ight. có tập nghiệm S. Khẳng định nào sau đây là khẳng định đúng?

    Ta có: \left\{ \begin{matrix} y - x > 3 \\ - 1 - x + y < 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} y > x + 3 \\ y < x + 1 \\ \end{matrix} ight.. Do đó không có điểm nào thỏa mãn hệ phương trình.

    Hệ này vô nghiệm.

  • Câu 6: Thông hiểu

    Tìm khẳng định đúng

    Biết phương trình \sqrt{x^{2} - 3x + 3} + \sqrt{x^{2} - 3x + 6} =3 có hai nghiệm x1, x2 (x1<x2) . Khẳng định nào sau đây là đúng?

    Đặt t = x2 − 3x + 3, ta có: t = \left( x - \frac{3}{2} ight)^{2}+ \frac{3}{4} \geq \frac{3}{4}.

    Do đó điều kiện cho ẩn phụ t là t \geq \frac{3}{4}.

    Khi đó phương trình trở thành:

    \sqrt{t} + \sqrt{t + 3} = 3\Leftrightarrow t + t + 3 +2\sqrt{t(t + 3)} = 9 ⇔ \sqrt{t(t + 3)} = 3 - t

    \Leftrightarrow \left\{ \begin{matrix}3 - t \geq 0 \\t(t + 3) = (3 - t)^{2} \\\end{matrix} ight. ⇔ \left\{ \begin{matrix}t \leq 3 \\t = 1 \\\end{matrix} ight.  ⇔ t = 1(thỏa mãn)

     ⇒ x2 − 3x + 3 = 1⇔ \left\lbrack \begin{matrix}x = 1 = x_{1} \\x = 2 = x_{2} \\\end{matrix} ight.\ \Rightarrow 2x_{1} = x_{2}.

  • Câu 7: Thông hiểu

    Tìm m thỏa mãn điều kiện

    Cho hàm số y = (m−1)x2 − 2(m−2)x + m − 3  (m≠1)(P). Đỉnh của (P) là S(−1;−2) thì m bằng bao nhiêu:

    Do đỉnh của (P) là S(−1;−2) suy ra - 1 = \frac{m - 2}{m - 1} \Leftrightarrow m = \frac{3}{2}.

  • Câu 8: Nhận biết

    Tìm bất phương trình thỏa mãn

    Cặp số (\ 1;\ - 1) là nghiệm của bất phương trình nào?

    Ta có: 1 + 4( - 1) = - 3 < 1.

  • Câu 9: Thông hiểu

    Tính độ dài cạnh AB

    Tam giác ABC có \widehat A = {105^0},\widehat B = {45^0};AC = 10. Độ dài cạnh AB là:

    Xét tam giác ABC ta có:

    \begin{matrix} \widehat A + \widehat B + \widehat C = {180^0} \hfill \\ \Rightarrow \widehat C = {180^0} - \left( {\widehat A + \widehat B} ight) = {30^0} \hfill \\ \end{matrix}

    Áp dụng định lí sin cho tam giác ABC ta có:

    \begin{matrix} \dfrac{{AC}}{{\sin \widehat B}} = \dfrac{{AB}}{{\sin \widehat C}} \hfill \\ \Rightarrow AB = \dfrac{{AC.\sin \widehat C}}{{\sin \widehat B}} = \dfrac{{10.\sin {{30}^0}}}{{\sin {{45}^0}}} = 5\sqrt 2 \hfill \\ \end{matrix}

  • Câu 10: Vận dụng cao

    Tính số tiền lãi lớn nhất

    Một nhà máy gồm hai đội công nhân (đội 1 và đội 2) sản xuất nhôm và sắt. Muốn sản xuất một tấn nhôm thì đội 1 phải làm việc trong 3 giờ và đội 2 làm việc trong 1 giờ. Một đội không thể sản xuất đồng thời nhôm và sắt. Đội 1 làm việc không quá 6 giờ một ngày, đội 2 làm việc không quá 4 giờ một ngày. Hỏi số tiền lãi lớn nhất mà nhà mhà máy thu về trong một ngày là bao nhiêu? Biết một tấn nhôm lãi 2 000 000 đồng, một tấn sắt lãi 1 600 000 triệu đồng.

    Gọi x, y lần lượt là số tấn nhôm và sắt mà nhà máy này sản xuất trong một ngày

    Điều kiện: x, y > 0

    Khi đó số tiền lãi một ngày của nhà máy này là f(x;y) = 2x + 1,6y (triệu đồng)

    Số giờ làm việc trong ngày của đội 1 là 3x + y (giờ)

    Số giờ làm việc trong ngày của đội 2 là x + y (giờ)

    Vì mỗi ngày đội 1 làm việc không quá 6 giờ và đội 2 làm việc không quá 4 giờ nên ta có hệ bất phương trình: \left\{ \begin{matrix} 3x + y \leq 6 \\ x + y \leq 4 \\ x,\ y \geq 0 \\ \end{matrix} ight.\ (*)

    Bài toán trở thành tìm giá trị lớn nhất của hàm số f(x;y) trên miền nghiệm của hệ bất phương trình (∗).

    Miền nghiệm của hệ bất phương trình (∗) là tứ giác OABC (kể cả biên).

    Hình vẽ minh họa

    Hàm số f(x;y) sẽ đạt giá trị lớn nhất trên miền nghiệm của hệ bất phương trình (∗) khi (x;y) là toạ độ một trong các đỉnh O(0;0),A(2;0),B(1;3),C(0;4).

    Ta có: \left\{ \begin{matrix} f(0;0) = 0 \\ f(2;0) = 4 \\ f(1;3) = 6,8 \\ f(0;4) = 6,4 \\ \end{matrix} ight.

    Suy ra max\ f(x;y) = 6,8 khi (x;y) = (1;3)

    Vậy số tiền lãi lớn nhất mà nhà máy thu được trong một ngày là: 6,8 triệu đồng.

  • Câu 11: Nhận biết

    Tìm tọa độ của vectơ thỏa mãn

    Trong hệ tọa độ Oxy, cho A(5;2),\ B(10;8). Tìm tọa độ của vectơ \overrightarrow{AB}?

    Ta có \overrightarrow{AB} = (5;6).

  • Câu 12: Vận dụng

    Tìm m thỏa mãn điều kiện

    Tìm m để g(x) = (2m2+m−6)x2 + (2m−3)x − 1 không dương.

    Xét 2m^{2} + m - 6 = 0 \Leftrightarrow \left\lbrack \begin{matrix} m = - 2 \\ m = \frac{3}{2} \\ \end{matrix} ight.

    +)m = - 2 \Rightarrow g(x) = - 7x - 1 > 0 \Leftrightarrow x < - \frac{1}{7} (không thỏa mãn yêu cầu bài toán)

    +) m = \frac{3}{2} \Rightarrow g(x) = 0 (không thỏa mãn)

    Xét 2m^{2} + m - 6 eq 0 \Leftrightarrow \left\{ \begin{matrix} m eq - 2 \\ m eq \frac{3}{2} \\ \end{matrix} ight.

    g(x) \leq 0,\ \ \forall x \Leftrightarrow \left\{ \begin{matrix} a = 2m^{2} + m - 6 < 0 \\ \Delta' = 12m^{2} - 8m - 15 \leq 0 \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} - 2 < m < \frac{3}{2} \\ - \frac{5}{6} \leq m \leq \frac{3}{2} \\ \end{matrix} ight.\ \Leftrightarrow - \frac{5}{6} \leq m < \frac{3}{2}

  • Câu 13: Vận dụng cao

    Tính bán kính đường tròn

    Cho tam giác đều ABC cạnh a. Biết rằng tập hợp các điểm M thỏa mãn đẳng thức \left| 2\overrightarrow{MA} + 3\overrightarrow{MB} + 4\overrightarrow{MC} \right| = \left| \overrightarrow{MB} - \overrightarrow{MA} \right| là đường tròn cố định có bán kính R. Tính bán kính R theo a.

    Gọi G là trọng tâm của tam giác ABC.

    Ta có 2\overrightarrow{MA} + 3\overrightarrow{MB} + 4\overrightarrow{MC} = 2\left( \overrightarrow{MI} + \overrightarrow{IA} \right) + 3\left( \overrightarrow{MI} + \overrightarrow{IB} \right) + 4\left( \overrightarrow{MI} + \overrightarrow{IC} \right).

    Chọn điểm I sao cho 2\overrightarrow{IA} + 3\overrightarrow{IB} + 4\overrightarrow{IC} = \overrightarrow{0}

    \Leftrightarrow 3\left( \overrightarrow{IA} + \overrightarrow{IB} + \overrightarrow{IC} \right) + \overrightarrow{IC} - \overrightarrow{IA} = \overrightarrow{0}.

    Mà G là trọng tâm của tam giác ABC \Rightarrow \overrightarrow{IA} + \overrightarrow{IB} + \overrightarrow{IC} = 3\ \overrightarrow{IG}.

    Khi đó 9\ \overrightarrow{IG} + \overrightarrow{IC} - \overrightarrow{IA} = \overrightarrow{0}

    \Leftrightarrow 9\ \overrightarrow{IG} + \overrightarrow{AI} + \overrightarrow{IC} = \overrightarrow{0} \Leftrightarrow 9\ \overrightarrow{IG} = \overrightarrow{CA}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (*).

    Do đó \left| 2\overrightarrow{MA} + 3\overrightarrow{MB} + 4\overrightarrow{MC} \right| = \left| \overrightarrow{MB} - \overrightarrow{MA} \right|

    \Leftrightarrow \left| 9\overrightarrow{MI} + 2\overrightarrow{IA} + 3\overrightarrow{IB} + 4\overrightarrow{IC} \right| = \left| \overrightarrow{AB} \right|

    \Leftrightarrow 9MI = AB.

    Vì I là điểm cố định thỏa mãn (*) nên tập hợp các điểm M cần tìm là đường tròn tâm I, bán kính r = \frac{AB}{9} = \frac{a}{9}.

  • Câu 14: Nhận biết

    Số nghiệm của phương trình là

    Số nghiệm của phương trình 3x + \sqrt{x - 8} = \sqrt{4 - x}. là bao nhiêu?

    Xét phương trình: 3x + \sqrt{x - 8} = \sqrt{4 - x}.

    Điều kiện: \left\{ \begin{matrix} x - 8 \geq 0 \\ 4 - x \geq 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x \geq 8 \\ x \leq 4 \\ \end{matrix} ight.\ \Leftrightarrow x \in \varnothing..

    Vậy phương trình vô nghiệm.

  • Câu 15: Vận dụng cao

    Xác định đặc điểm tam giác ABC

    Cho tam giác ABC có các góc thỏa mãn biểu thức

    \sin2\widehat{A} + \sin2\widehat{B} =\dfrac{\sin2\widehat{A}.\sin2\widehat{B}}{\cos\widehat{A}.\cos\widehat{B}}

    Khi đó tam giác ABC là tam giác gì?

    Ta có:

    \sin2\widehat{A} + \sin2\widehat{B} =\frac{\sin2\widehat{A}.\sin2\widehat{B}}{\cos\widehat{A}.\cos\widehat{B}}

    \Leftrightarrow2\sin\widehat{A}.\cos\widehat{A} + 2\sin\widehat{B}.\cos\widehat{B} =\frac{2\sin\widehat{A}.\cos\widehat{A}.2\sin\widehat{B}.\cos\widehat{B}}{\cos\widehat{A}.\cos\widehat{B}}

    \Leftrightarrow\sin\widehat{A}.\cos\widehat{A} + \sin\widehat{B}.\cos\widehat{B} =2\sin\widehat{A}.\sin\widehat{B}

    \Leftrightarrow \sin2\widehat{A} +\sin2\widehat{B} = 4\sin\widehat{A}.\sin\widehat{B}

    \Leftrightarrow 2\sin\left( \widehat{A} +\widehat{B} ight).\cos\left( \widehat{A} - \widehat{B} ight) =2\left\lbrack \cos\left( \widehat{A} - \widehat{B} ight) - \cos\left(\widehat{A} + \widehat{B} ight) ightbrack

    \Leftrightarrow\sin\widehat{C}.\cos\left( \widehat{A} - \widehat{B} ight) = \cos\left(\widehat{A} - \widehat{B} ight) + \cos\left( \widehat{C}ight)

    \Leftrightarrow \cos\widehat{C}.\left( 1- \sin\widehat{C} ight).\cos\left( \widehat{A} - \widehat{B} ight) +\cos^{2}\left( \widehat{C} ight) = 0

    \Leftrightarrow \cos\widehat{C}.\left( 1- \sin\widehat{C} ight).\cos\left( \widehat{A} - \widehat{B} ight) +1 - \sin^{2}\left( \widehat{C} ight) = 0

    \Leftrightarrow \left( 1 - \sin\widehat{C} ight).\left\lbrack \cos\left( \widehat{A} - \widehat{B} ight)\cos\widehat{C} + 1 + \sin\widehat{C}. ightbrack = 0

    \Leftrightarrow 1 - \sin\widehat{C} = 0

    \Leftrightarrow \widehat{C} = \frac{\pi}{2}

    Vậy tam giác ABC là tam giác vuông.

  • Câu 16: Thông hiểu

    Xác định câu đúng

    Gọi AN,\ CM là các trung tuyến của tam giác ABC. Đẳng thức nào sau đây đúng?

    Hình vẽ minh họa:

    Ta có \overrightarrow{AN} = \frac{1}{2}\left( \overrightarrow{AB} + \overrightarrow{AC} \right) = \frac{1}{2}\overrightarrow{AB} + \frac{1}{2}\overrightarrow{AC}

    \overrightarrow{CM} = \overrightarrow{CA} + \overrightarrow{AM} \Rightarrow \frac{1}{2}\overrightarrow{CM} = \frac{1}{2}\overrightarrow{CA} + \frac{1}{2}\overrightarrow{AM}

    Suy ra \overrightarrow{AN} + \frac{1}{2}\overrightarrow{CM} = \frac{1}{2}\overrightarrow{AB} + \frac{1}{2}\overrightarrow{AC} + \frac{1}{2}\overrightarrow{CA} + \frac{1}{2}\overrightarrow{AM}

    = \frac{1}{2}\overrightarrow{AB} + \frac{1}{2}\overrightarrow{AC} - \frac{1}{2}\overrightarrow{AC} + \frac{1}{2} \cdot \frac{1}{2}\overrightarrow{AB} = \frac{3}{4}\overrightarrow{AB}

    Do đó \overrightarrow{AB} = \frac{4}{3}\overrightarrow{AN} + \frac{2}{3}\overrightarrow{CM}.

  • Câu 17: Vận dụng

    Đẳng thức nào sau đây sai?

    Cho lục giác đều ABCDEF có tâm O. Đẳng thức nào sau đây sai?

    Ta có

    \bullet \overrightarrow{OA} + \overrightarrow{OC} + \overrightarrow{OE} = \left( \overrightarrow{OA} + \overrightarrow{OC} ight) + \overrightarrow{OE} = \overrightarrow{OB} + \overrightarrow{OE} = \overrightarrow{0}. Do đo \overrightarrow{OA} + \overrightarrow{OC} + \overrightarrow{OE} = \overrightarrow{0}. đúng.

    \bullet \overrightarrow{OA} + \overrightarrow{OC} + \overrightarrow{OB} = \left( \overrightarrow{OA} + \overrightarrow{OC} ight) + \overrightarrow{OB}

    = \overrightarrow{OB} + \overrightarrow{OB} = 2\overrightarrow{OB} = \overrightarrow{EB}. Do đo \overrightarrow{OA} + \overrightarrow{OC} + \overrightarrow{OB} = \overrightarrow{EB} đúng.

    \bullet \overrightarrow{AB} + \overrightarrow{CD} + \overrightarrow{EF} = \left( \overrightarrow{AB} + \overrightarrow{CD} ight) + \overrightarrow{EF} = \left( \overrightarrow{AB} + \overrightarrow{BO} ight) + \overrightarrow{EF}

    = \overrightarrow{AO} + \overrightarrow{EF} = \overrightarrow{AO} + \overrightarrow{OA} = \overrightarrow{AA} = \overrightarrow{0}. Do đó \overrightarrow{AB} + \overrightarrow{CD} + \overrightarrow{EF} = \overrightarrow{0} đúng.

    Dùng phương pháp loại trừ, suy ra \overrightarrow{BC} + \overrightarrow{EF} = \overrightarrow{AD} sai.

  • Câu 18: Vận dụng cao

    Tìm số giá trị của m thỏa mãn điều kiện

    Đường thẳng d : y = (m−3)x − 2m + 1 cắt hai trục tọa độ tại hai điểm A và B sao cho tam giác OAB cân. Khi đó, số giá trị của m thỏa mãn là

    A = d ∩ Ox nên tọa độ A là nghiệm của hệ:

    \left\{ \begin{matrix} y = (m - 3)x - 2m + 1 \\ y = 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x = \frac{2m - 1}{m - 3} \\ y = 0 \\ \end{matrix} ight. nên A\left( \frac{2m - 1}{m - 3};\ 0 ight).

    B = d ∩ Oy nên tọa độ B là nghiệm của hệ:

    \left\{ \begin{matrix} y = (m - 3)x - 2m + 1 \\ x = 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x = 0 \\ y = - 2m + 1 \\ \end{matrix} ight. nên B(0;−2m+1).

    Ta có OA = OB \Leftrightarrow \left| \frac{2m - 1}{m - 3} ight| = | - 2m + 1| \Leftrightarrow |2m - 1|\left( \frac{1}{|m - 3|} - 1 = 0 ight)

    \Leftrightarrow \left\lbrack \begin{matrix} 2m - 1 = 0 \\ |m - 3| = 1 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} m = \frac{1}{2} \\ m = 4,\ m = 2 \\ \end{matrix} ight..

    Nhận xét: Với m = \frac{1}{2}thì A ≡ B ≡ O(0;  0) nên không thỏa mãn.

    Vậy m = 4, m = 2.

  • Câu 19: Vận dụng

    Chiều cao của cây gần nhất với giá trị nào sau đây

    Từ vị trí A người ta quan sát một cây cao (hình vẽ).

    Biết AH = 4m,HB = 20m,\widehat{BAC} = 45^{0}.

    Chiều cao của cây gần nhất với giá trị nào sau đây?

    Trong tam giác AHB, ta có \tan\widehat{ABH} = \frac{AH}{BH} = \frac{4}{20} = \frac{1}{5} \overset{}{ightarrow}\widehat{ABH} \approx 11^{0}19'.

    Suy ra \widehat{ABC} = 90^{0} - \widehat{ABH} = 78^{0}41'.

    Suy ra \widehat{ACB} = 180^{0} - \left( \widehat{BAC} + \widehat{ABC} ight) = 56^{0}19'.

    Áp dụng định lý sin trong tam giác ABC, ta được \frac{AB}{\sin\widehat{ACB}} = \frac{CB}{\sin\widehat{BAC}} \overset{}{ightarrow}CB = \frac{AB.sin\widehat{BAC}}{\sin\widehat{ACB}} \approx 17m.

  • Câu 20: Vận dụng cao

    Tìm khẳng định đúng

    Biết phương trình (x + 5)(2 - x) = 3\sqrt{x^{2} + 3x}có 2 nghiệm x1, x2 (x1<x2) . Khẳng định nào sau đây đúng?

    Điều kiện:

    x2 + 3x ≥ 0⇔ \left\lbrack \begin{matrix} x \leq - 3 \\ x \geq 0 \\ \end{matrix} ight.\ (1)

    phương trình \Leftrightarrow x^{2} + 3x + 3\sqrt{x^{2} + 3x} - 10 = 0.

    Đặt t = \sqrt{x^{2} + 3x}, điều kiện t ≥ 0.

    Phương trình trở thành t2 + 3t − 10 = 0

    ⇔ \left\lbrack \begin{matrix} t = 2(TM) \\ t = - 5(KTM) \\ \end{matrix} ight. ⇒ \sqrt{x^{2} + 3x} = 2 \Leftrightarrow x^{2} + 3x - 4 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 = x_{2} \\ x = - 4 = x_{1} \\ \end{matrix} ight., thoả mãn (1) ⇒ x1 + 4x2 = 0.

  • Câu 21: Nhận biết

    Tìm đẳng thức sai

    Gọi O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD. Đẳng thức nào sau đây là đẳng thức sai?

    Ta có: \overrightarrow {DB} = 2\overrightarrow {OB}.

    Vậy đẳng thức sai là:  \overrightarrow{DB} = 2\overrightarrow{BO} .

  • Câu 22: Vận dụng

    Tìm hình vẽ thỏa mãn

    Miền nghiệm của hệ bất phương trình \left\{ \begin{matrix} x + y - 1 > 0 \\ y \geq 2 \\ - x + 2y > 3 \\ \end{matrix} ight. là phần không tô đậm của hình vẽ nào trong các hình vẽ sau?

    Xét điểm M(0;4) thử vào các bất phương trình của hệ thấy thỏa mãn.

    Chỉ có hình vẽ chứa điểm M(0;4). Chọn đáp án hình vẽ này.

  • Câu 23: Nhận biết

    Tam thức bậc hai nhận giá trị không âm khi và chỉ khi

    Tam thức bậc hai f(x) =  − x2 + 3x − 2 nhận giá trị không âm khi và chỉ khi

    f(x) = - x^{2} + 3x - 2 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = 2 \\ \end{matrix} ight.

    Dựa vào bảng xét dấu, ta chọn đáp ánx ∈ [1; 2] .

  • Câu 24: Thông hiểu

    Tìm các điểm thẳng hàng

    Trong hệ tọa độ Oxy, cho bốn điểm A(3;0),B(4; - 3),C(8; - 1),D( - 2;1). Các điểm nào trong các điểm đã cho thẳng hàng với nhau?

    Ta có:

    \left\{ \begin{matrix} \overrightarrow{AC} = (5; - 1) \\ \overrightarrow{AD} = ( - 5;1) \\ \end{matrix} ight.\ \Rightarrow \overrightarrow{AC} = - \overrightarrow{AD}

    Vậy ba điểm A,C,D thẳng hàng.

  • Câu 25: Thông hiểu

    Tìm khẳng định đúng

    Trong mặt phẳng Oxy cho A( - 1;1), B(1;3), C(1; - 1). Khẳng định nào sau đây đúng.

    Phương án \overrightarrow{AB} = (4;2), \overrightarrow{BC} = (2; - 4): do \overrightarrow{AB} = (2;2) nên loại đáp án này.

    Phương án \overrightarrow{AB}\bot\overrightarrow{BC}:

    \overrightarrow{AB} = (2;2),\overrightarrow{BC} = (0; - 4), \overrightarrow{AB}.\overrightarrow{BC} = - 8 suy ra \overrightarrow{AB} không vuông góc \overrightarrow{BC} nên loại đáp án này.

    Phương án tam giác ABC vuông cân tại A:

    Ta có \overrightarrow{AB} = (2;2), \overrightarrow{AC} = (2; - 2), \overrightarrow{BC} = (0; - 4), suy ra AB = AC = \sqrt{8}, \overrightarrow{AB}.\overrightarrow{AC} = 0.

    Nên tam giác ABC vuông cân tại A.

    Do đó chọn đáp án này.

  • Câu 26: Nhận biết

    Phát biểu mệnh đề

    Mệnh đề "\ \exists x\mathbb{\in R},\ x^{2} = 3" khẳng định rằng:

    Phát biểu mệnh đề như sau: “Có ít nhất một số thực mà bình phương của nó bằng 3”.

  • Câu 27: Thông hiểu

    Tìm a thỏa mãn điều kiện

    Với giá trị nào của a thì ax2 − x + a ≥ 0, ∀x ∈ ℝ?

    *a = 0thì bpt trở thành  − x ≥ 0 ⇔ x ≤ 0. Suy ra a = 0không thỏa ycbt.

    * a ≠ 0 thì ax^{2} - x + a \geq 0,\forall x\mathbb{\in R \Leftrightarrow}\left\{ \begin{matrix} \Delta \leq 0 \\ a > 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} 1 - 4a^{2} \leq 0 \\ a > 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} \left\lbrack \begin{matrix} a \geq \frac{1}{2} \\ a \leq - \frac{1}{2} \\ \end{matrix} ight.\ \\ a > 0 \\ \end{matrix} ight.\ \Leftrightarrow a \geq \frac{1}{2}.

  • Câu 28: Thông hiểu

    Chọn đẳng thức đúng

    Cho tam giác ABC có AB = AC và đường cao AH. Đẳng thức nào sau đây đúng?

    Hình vẽ minh họa

    Do \Delta ABC cân tại A, AH là đường cao nên H là trung điểm BC.

    Xét các đáp án:

    Đáp án \overrightarrow{AB} + \overrightarrow{AC} = \overrightarrow{AH}. Ta có \overrightarrow{AB} + \overrightarrow{AC} = 2\overrightarrow{AH}.

    Đáp án \overrightarrow{HA} + \overrightarrow{HB} + \overrightarrow{HC} = \overrightarrow{0}. Ta có \overrightarrow{HA} + \overrightarrow{HB} + \overrightarrow{HC} = \overrightarrow{HA} + \overrightarrow{0} = \overrightarrow{HA} \neq \overrightarrow{0}.

    Đáp án \overrightarrow{HB} + \overrightarrow{HC} = \overrightarrow{0}. Ta có \overrightarrow{HB} + \overrightarrow{HC} = \overrightarrow{0} (H là trung điểm BC).

    Đáp án \overrightarrow{AB} = \overrightarrow{AC}. Do \overrightarrow{AB} và \overrightarrow{AC} không cùng hướng nên \overrightarrow{AB} \neq \overrightarrow{AC}.

  • Câu 29: Nhận biết

    Tìm công thức của Parabol

    Tìm parabol (P) : y = ax2 + 3x − 2, biết rằng parabol cắt trục Ox tại điểm có hoành độ bằng 2.

    Vì (P) cắt trục Ox tại điểm có hoành độ bằng 2 nên điểm A(2;0) thuộc (P). Thay \left\{ \begin{matrix} x = 2 \\ y = 0 \\ \end{matrix} ight. vào (P), ta được 0 = 4a + 6 − 2 ⇔ a =  − 1.

    Vậy (P) : y =  − x2 + 3x − 2.

  • Câu 30: Thông hiểu

    Xét tính đúng sai của các khẳng định

    Cho tam giác ABC có G là trọng tâm. Gọi D là điểm đối xứng của B qua G và M là trung điểm của BC. Khi đó:

    a) \overrightarrow{MD} = \overrightarrow{MG} + \overrightarrow{GD}. Đúng||Sai

    b) \overrightarrow{AG} = 2\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AC}. Sai||Đúng

    c) \overrightarrow{CD} = \overrightarrow{AB} - \overrightarrow{AC} + \frac{1}{3}\overrightarrow{BG}. Sai||Đúng

    d) \overrightarrow{MD} = - \frac{5}{6}\overrightarrow{AB} + \frac{1}{6}\overrightarrow{AC}. Đúng||Sai

    Đáp án là:

    Cho tam giác ABC có G là trọng tâm. Gọi D là điểm đối xứng của B qua G và M là trung điểm của BC. Khi đó:

    a) \overrightarrow{MD} = \overrightarrow{MG} + \overrightarrow{GD}. Đúng||Sai

    b) \overrightarrow{AG} = 2\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AC}. Sai||Đúng

    c) \overrightarrow{CD} = \overrightarrow{AB} - \overrightarrow{AC} + \frac{1}{3}\overrightarrow{BG}. Sai||Đúng

    d) \overrightarrow{MD} = - \frac{5}{6}\overrightarrow{AB} + \frac{1}{6}\overrightarrow{AC}. Đúng||Sai

    a) \overrightarrow{MD} = \overrightarrow{MG} + \overrightarrow{GD} .

    Ta có: \overrightarrow{MD} = \overrightarrow{MG} + \overrightarrow{GD}.

    b) \overrightarrow{AG} = 2\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AC}.

    Ta có: \overrightarrow{AG} = \frac{2}{3}\overrightarrow{AM} = \frac{2}{3} \cdot \frac{1}{2}\left( \overrightarrow{AB} + \overrightarrow{AC} \right) = \frac{1}{3}\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AC}.

    c) \overrightarrow{CD} = \overrightarrow{AB} - \overrightarrow{AC} + \frac{1}{3}\overrightarrow{BG}.

    Ta có: \overrightarrow{CD} = \overrightarrow{CB} + \overrightarrow{BD} = \overrightarrow{AB} - \overrightarrow{AC} + \frac{1}{2}\overrightarrow{BG}

    d) \overrightarrow{MD} = - \frac{5}{6}\overrightarrow{AB} + \frac{1}{6}\overrightarrow{AC}.

    Ta có:

    \overrightarrow{MD} = \overrightarrow{MG} + \overrightarrow{GD} = -\frac{1}{3}\overrightarrow{AM} + \overrightarrow{BG}

    = - \frac{1}{3}\cdot \frac{1}{2}\left( \overrightarrow{AB} + \overrightarrow{AC}\right) + \left( \overrightarrow{BA} + \frac{2}{3}\overrightarrow{AM}\right)

    = - \frac{1}{6}\overrightarrow{AB} - \frac{1}{6}\overrightarrow{AC} -\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AB} +\frac{1}{3}\overrightarrow{AC}

    = - \frac{5}{6}\overrightarrow{AB} +\frac{1}{6}\overrightarrow{AC}

  • Câu 31: Nhận biết

    Tìm hàm số bậc hai

    Trong các hàm số sau, hàm số nào là hàm số bậc hai?

    Đáp án y = x^{2} + 2x – 1 là đáp án đúng vì hàm số bậc hai có dạng y = a{x^2} + bx + c;\left( {a e 0} ight)

  • Câu 32: Nhận biết

    Tìm đẳng thức đúng

    Trong các đẳng thức sau đây, đẳng thức nào đúng?

    Mối liên hệ hai cung bù nhau.

  • Câu 33: Nhận biết

    Chọn đẳng thức đúng

    Cho hình bình hành ABCD, với giao điểm hai đường chéo I. Khi đó:

     Ta có: \overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{0} (2 vectơ đối nhau).

  • Câu 34: Thông hiểu

    Chọn đáp án đúng

    Tam giác với ba cạnh là 5;12;13 có bán kính đường tròn nội tiếp tam giác đó bằng bao nhiêu?

    Ta có: p = \frac{5 + 12 + 13}{2} = 15.

    Mà 5^{2} + 12^{2} = 13^{2} \Rightarrow S = \frac{1}{2}.5.12 = 30.

    Mặt khác S = p.r \Rightarrow r = \frac{S}{p} = 2.

  • Câu 35: Thông hiểu

    Xác định tập hợp X

    Cho C_{R}A = ( -\infty;2) \cup \lbrack 6; + \infty) và C_{R}B = \lbrack 5;9). Tập hợp X = A \cap B là

    A = \lbrack 2;6),B = ( - \infty;5) \cup\lbrack 9; + \infty).

    Suy ra X = A \cap B = \lbrack2;5).

  • Câu 36: Thông hiểu

    Chọn khẳng định đúng

    Cho A là tập hợp các bội của 2, B là tập hợp các bội của 8. Chọn khẳng định đúng:

     Số lượng phần tử của tập hợp các bội của 2 nhiều hơn số lượng phần tử tập hợp các bội của 8. Mà đã là bội của 8 thì cũng là bội của 2. 

    Do đó B\subset A

  • Câu 37: Nhận biết

    Mệnh đề nào sau đây đúng?

    Cho tam giác ABC với M là trung điểm BC. Mệnh đề nào sau đây đúng?

    Xét đáp án \overrightarrow{AM} + \overrightarrow{MB} + \overrightarrow{BA} = \overrightarrow{0}. Ta có \overrightarrow{AM} + \overrightarrow{MB} + \overrightarrow{BA} = \overrightarrow{0} (theo quy tắc ba điểm).

    Chọn đáp án này.

  • Câu 38: Nhận biết

    Tìm đẳng thức sai

    Đẳng thức nào sau đây sai?

    Giá trị lượng giác của góc đặc biệt ta có:

    \left\{ \begin{matrix}\sin120^{0} = \dfrac{\sqrt{3}}{2} \\\cos30^{0} = \dfrac{\sqrt{3}}{2}\end{matrix} \right.\ \Rightarrow \sin120^{0} + \cos30^{0} =2.\dfrac{\sqrt{3}}{2} = \sqrt{3} \neq 0

    Vậy đẳng thức sai là: sin120^{0} + cos30^{0} = 0.

  • Câu 39: Nhận biết

    Tìm vectơ thỏa mãn

    Cho hình bình hành ABCD, vectơ có điểm đầu và điểm cuối là các đỉnh của hình bình hành bằng với vectơ \overrightarrow{AB} là:

    Ta có ABCD là hình bình hành nên \left\{ \begin{matrix} AB = CD \\ AB \parallel CD \\ \end{matrix} ight. do đó \overrightarrow{AB} = \overrightarrow{DC}.

  • Câu 40: Thông hiểu

    Tính giá trị của hàm số tại điểm

    Cho hàm số y=\left\{\begin{matrix}\frac{2}{x-1},x\in (-∞;0) \\ \sqrt{x+1},x\in [0;2]\\ x^{2}-1,x\in (2;5]\end{matrix}ight.. Tính f(4), ta được kết quả:

     Với x=4 \in (2;5], ta có: f(4)=4^2-1=15.

  • Câu 41: Thông hiểu

    Tìm tập nghiệm của bất phương trình

    Giải bất phương trình \frac{{5{x^2} + 3x - 8}}{{{x^2} - 7x + 6}} \leqslant 0

    Ta có bảng xét dấu như sau:

    Tìm tập nghiệm của bất phương trình

    Vậy tập nghiệm của bất phương trình là: S = \left[ {\frac{{ - 8}}{5};1} ight) \cup \left( {1;6} ight)

  • Câu 42: Vận dụng

    Tính tích vô hướng

    Cho 2 vectơ đơn vị \overrightarrow{a} và \overrightarrow{b} thỏa\left| \overrightarrow{a} + \overrightarrow{b} ight| = 2. Hãy xác định \left( 3\overrightarrow{a} - 4\overrightarrow{b} ight)\left( 2\overrightarrow{a} + 5\overrightarrow{b} ight).

    Ta có: \left| \overrightarrow{a} ight| = \left| \overrightarrow{b} ight| = 1 và \left| \overrightarrow{a} + \overrightarrow{b} ight| = 2 \Leftrightarrow \left( \overrightarrow{a} + \overrightarrow{b} ight)^{2} = 4 \Leftrightarrow \overrightarrow{a}.\overrightarrow{b} = 1 .

    Suy ra \left( 3\overrightarrow{a} -4\overrightarrow{b} ight)\left( 2\overrightarrow{a} +5\overrightarrow{b} ight)= 6{\overrightarrow{a}}^{2} -20{\overrightarrow{b}}^{2} + 7\overrightarrow{a}.\overrightarrow{b} = -7.

  • Câu 43: Nhận biết

    Các kí hiệu nào sau đây dùng để viết đúng mệnh đề “7 là một số tự nhiên”

    Các kí hiệu nào sau đây dùng để viết đúng mệnh đề “7 là một số tự nhiên”:

    Ta có: \mathbf{7}\mathbb{\in N}\mathbf{.}

  • Câu 44: Vận dụng

    Xác định dấu của biểu thức

    Cho \pi < \alpha < \frac{3\pi}{2}. Xác định dấu của biểu thức M = \sin\left( \frac{\pi}{2} - \alpha ight).cot(\pi + \alpha).

    Ta có:

    \left\{ \begin{matrix} \pi < \alpha < \frac{3\pi}{2} ightarrow - \frac{3\pi}{2} < - \alpha < - \pi \\ \pi < \alpha < \frac{3\pi}{2} ightarrow 2\pi < \pi + \alpha < \frac{5\pi}{2} \\ \end{matrix} ight. ightarrow - \pi < \frac{\pi}{2} - \alpha < - \frac{\pi}{2} và \overset{}{ightarrow}\cot(\pi + \alpha) > 0

    \overset{}{ightarrow}\sin\left( \frac{\pi}{2} - \alpha ight) < 0

    \overset{}{ightarrow}M < 0.

  • Câu 45: Thông hiểu

    Tìm câu sai

    Trong các mệnh đề sau, mệnh đề nào sai?

    Ta có:

    Mệnh đề “\exists n\mathbb{\in N}, n^{2} + 11n + 2 chia hết cho 11” đúng với n = 3.

    Mệnh đề “Tồn tại số nguyên tố chia hết cho 5” đúng với số nguyên tố là 5.

    Mệnh đề “\exists n\mathbb{\in Z}, 2n^{2} - 8 = 0” đúng với n = \pm 2.

    Mệnh đề “\exists n\mathbb{\in N}, n^{2} + 1 chia hết cho 4” sai: Do n \in N nên \left\lbrack \begin{matrix} n = 2k \\ n = 2k + 1 \\ \end{matrix} \right.\ (k \in N) \Rightarrow \left\lbrack \begin{matrix} n^{2} + 1 = 4k^{2} + 1 \\ n^{2} + 1 = 4k^{2} + 4k + 2 \\ \end{matrix} \right. đều không chia hết cho 4 với\forall k \in N.

Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi học kì 1 Toán 10 Cánh Diều Đề 3 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
  • Điểm thưởng: 0
Xem đáp án Làm lại
1
21 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Đề thi học kì 1 Toán 10 Cánh Diều Đề 3
Thời gian còn lại 90:00 Số câu đã làm 0/45
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
Chưa làm Đã làm
Làm lại Nộp bài
Tìm bài trong mục này
🖼️

Toán 10 - Cánh diều
Xem thêm