VnDoc.com Lớp 10 Khóa học Lớp 10 Toán 10 - Cánh diều

Đóng

Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm

Mua VnDoc PRO chỉ từ 79.000đ

Đóng

Bạn cần đăng nhập tài khoản Thành viên VnDoc để:

- Xem đáp án

- Nhận 1 lần làm bài trắc nghiệm miễn phí!

Đăng nhập

Đề kiểm tra 45 phút Chương 4 Hệ thức lượng trong tam giác. Vectơ

Mô tả thêm:

Đề kiểm tra 45 phút Toán 10 Chương 4 Hệ thức lượng trong tam giác. Vectơ sách Cánh Diều giúp bạn học tổng hợp lại kiến thức của cả nội dung chương. Cùng nhau luyện tập nha!

Thời gian làm: 45 phút
Số câu hỏi: 40 câu
Số điểm tối đa: 40 điểm
Tài khoản: Đăng nhập

Trước khi làm bài bạn hãy

1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
4 Căn chỉnh thời gian làm từng câu một cách hợp lý

Bắt đầu làm bài

Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay

Câu 1: Nhận biết
Điều kiện cần và đủ để ba điểm thẳng hàng.

Cho ba điểm $A,\ B,\ C$ phân biệt. Điều kiện cần và đủ để ba điểm đó thẳng hàng là
- A.
  $\forall M:\overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} = \overrightarrow{0}$ .
- B.
  $\forall M:\overrightarrow{MA} + \overrightarrow{MC} = \overrightarrow{MB}$ .
- C.
  $\overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{BC}$ .
- D.
  $\exists k \in R:\overrightarrow{AB} = k\overrightarrow{AC}$ .
Ta có tính chất: Điều kiện cần và đủ để ba điểm $A,\ B,\ C$ phân biệt thẳng hàng là $\exists k \in R:\overrightarrow{AB} = k\overrightarrow{AC}$ .
Câu 2: Thông hiểu

Xét tính đúng sai của các khẳng định

Trong mặt phẳng tọa độ $Oxy$ , cho các vectơ $\overrightarrow{a} = (2; - 2),\overrightarrow{b} = (4;1)$ và $\overrightarrow{c} = (0; - 1)$ .

Khi đó:

a) $2\overrightarrow{a} - \overrightarrow{b} - 3\overrightarrow{c} = (0; - 2)$ . Đúng||Sai

b) Vectơ $\overrightarrow{e} = (1; - 1)$ cùng phương, cùng hướng với vectơ $\overrightarrow{a}$ . Đúng||Sai

c) Vectơ $\overrightarrow{f} = \left( - 1; - \frac{1}{4} \right)$ cùng phương, cùng hướng với vectơ $\overrightarrow{b}$ . Sai||Đúng

c) $\overrightarrow{a} = \frac{1}{2}\overrightarrow{b} + \frac{5}{2}\overrightarrow{c}$ .Đúng||Sai

Đáp án là:

Trong mặt phẳng tọa độ $Oxy$ , cho các vectơ $\overrightarrow{a} = (2; - 2),\overrightarrow{b} = (4;1)$ và $\overrightarrow{c} = (0; - 1)$ .

Khi đó:

a) $2\overrightarrow{a} - \overrightarrow{b} - 3\overrightarrow{c} = (0; - 2)$ . Đúng||Sai

b) Vectơ $\overrightarrow{e} = (1; - 1)$ cùng phương, cùng hướng với vectơ $\overrightarrow{a}$ . Đúng||Sai

c) Vectơ $\overrightarrow{f} = \left( - 1; - \frac{1}{4} \right)$ cùng phương, cùng hướng với vectơ $\overrightarrow{b}$ . Sai||Đúng

c) $\overrightarrow{a} = \frac{1}{2}\overrightarrow{b} + \frac{5}{2}\overrightarrow{c}$ .Đúng||Sai

Tổng quan đáp án

a) Đúng

b) Đúng

c) Sai

d) Đúng

Ta có: $\left\{ \begin{matrix} 2\overrightarrow{a} = (4; - 4) \\ - \overrightarrow{b} = ( - 4; - 1) \\ - 3\overrightarrow{c} = (0;3) \end{matrix} \Rightarrow \overrightarrow{d} = 2\overrightarrow{a} - \overrightarrow{b} - 3\overrightarrow{c} = (0; - 2) \right.$ .

Ta $\overrightarrow{a} = (2; - 2) = 2\overrightarrow{e}$ nên $\overrightarrow{a},\overrightarrow{e}$ là hai vectơ cùng phương với nhau, hơn nữa chúng cùng hướng với nhau vì $\overrightarrow{a} = k\overrightarrow{e},k = 2 > 0$ .

Tương tự : $\overrightarrow{b} = (4;1) = - 4\overrightarrow{f}$ , tức là $\overrightarrow{b} = k\overrightarrow{f},k = - 4 < 0$ nên $\overrightarrow{b}$ và $\overrightarrow{f}$ là hai vectơ cùng phương, ngược hướng với nhau.

Gọi $m,n$ là các số thỏa mãn $\overrightarrow{a} = m\overrightarrow{b} + n\overrightarrow{c}$ ( $\overrightarrow{b},\overrightarrow{c}$ không cùng phương).

Khi đó: $\left\{ \begin{matrix} 2 = m \cdot 4 + n \cdot 0 \\ - 2 = m \cdot 1 + n \cdot ( - 1) \end{matrix} \Leftrightarrow \left\{ \begin{matrix} m = \frac{1}{2} \\ n = \frac{5}{2} \end{matrix} \right.\ \right.$ .

Vậy $\overrightarrow{a} = \frac{1}{2}\overrightarrow{b} + \frac{5}{2}\overrightarrow{c}$ .
Câu 3: Nhận biết
Tìm câu sai

Cho ba điểm $A,\ B,\ C$ phân biệt. Đẳng thức nào sau đây là đẳng thức sai?
- A.
  $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}$ .
- B.
  $\overrightarrow{CA} + \overrightarrow{AB} = \overrightarrow{BC}$ .
- C.
  $\overrightarrow{BA} + \overrightarrow{AC} = \overrightarrow{BC}$ .
- D.
  $\overrightarrow{AB} - \overrightarrow{AC} = \overrightarrow{CB}$ .
Ta có: $\overrightarrow{CA} + \overrightarrow{AB} = \overrightarrow{CB} \neq \overrightarrow{BC}$ .
Câu 4: Nhận biết
Hãy chọn kết quả đúng

Điểm cuối của $\alpha$ thuộc góc phần tư thứ nhất của đường tròn lượng giác. Hãy chọn kết quả đúng trong các kết quả sau đây.
- A.
  $\sin\alpha > 0.$
- B.
  $\cos\alpha < 0.$
- C.
  $\tan\alpha < 0.$
- D.
  $\cot\alpha < 0.$
Điểm cuối của $\alpha$ thuộc góc phần tư thứ nhất $ightarrow \left\{ \begin{matrix} \sin\alpha > 0 \\ \cos\alpha > 0 \\ \tan\alpha > 0 \\ \cot\alpha > 0 \\ \end{matrix} ight.$ .
Câu 5: Nhận biết
Chọn khẳng định đúng

Cho hình bình hành $ABCD$ có tâm $O$ . Khẳng định nào sau đây là đúng:
- A.
  $\overrightarrow{AO} + \overrightarrow{BO} = \overrightarrow{BD}$ .
- B.
  $\overrightarrow{AO} + \overrightarrow{AC} = \overrightarrow{BO}$ .
- C.
  $\overrightarrow{AO} - \overrightarrow{BO} = \overrightarrow{CD}$ .
- D.
  $\overrightarrow{AB} - \overrightarrow{AC} = \overrightarrow{DA}$ .
Ta có: $\overrightarrow{AB} - \overrightarrow{AC} = \overrightarrow{CB} = \overrightarrow{DA}$ .
Câu 6: Nhận biết
Tìm đẳng thức sai

Cho hình bình hành $ABCD$ . Đẳng thức nào sau đây sai.
- A.
  $\left| \overrightarrow{AB} \right| = \left| \overrightarrow{CD} \right|$ .
- B.
  $\left| \overrightarrow{BC} \right| = \left| \overrightarrow{DA} \right|$ .
- C.
  $\left| \overrightarrow{AC} \right| = \left| \overrightarrow{BD} \right|$ .
- D.
  $\left| \overrightarrow{AD} \right| = \left| \overrightarrow{BC} \right|$ .
Ta có: $\left| \overrightarrow{AC} \right| = \left| \overrightarrow{BD} \right|$ sai do $ABCD$ là hình bình hành.
Câu 7: Nhận biết
Tính tích vô hướng

Cho các vectơ $\overrightarrow{a} = (1; - 3),\ \ \overrightarrow{b} = (2;5)$ . Tính tích vô hướng của $\overrightarrow{a}\left( \overrightarrow{a} + 2\overrightarrow{b} \right)$ ?
- A.
  $16$ .
- B.
  $26$ .
- C.
  $36$ .
- D.
  $- 16$ .
Ta có:

$\overrightarrow{a}.\overrightarrow{a} = 10$ , $\overrightarrow{a}.\overrightarrow{b} = - 13$ suy ra $\overrightarrow{a}\left( \overrightarrow{a} + 2\overrightarrow{b} \right) = - 16$ .
Câu 8: Nhận biết
Tính diện tích tam giác ABC

Cho tam giác $ABC$ có $AB = 12,AC = 13,BC = 5$ . Diện tích $S$ của tam giác $ABC$ là:
- A.
  $S = 30$ .
- B.
  $S = 40$ .
- C.
  $S = 50$ .
- D.
  $S = 60$ .
Ta có: $BA^{2} + BC^{2} = AC^{2}$ nên tam giác $ABC$ vuông tại B.

Diện tích tam giác là: $S = \frac{1}{2}BA \cdot BC = 30$ .
Câu 9: Thông hiểu
Đẳng thức nào sau đây đúng?

Gọi $M,\ \ N$ lần lượt là trung điểm của các cạnh $AB,\ \ AC$ của tam giác đều $ABC$ . Đẳng thức nào sau đây đúng?
- A.
  $\overrightarrow{MA} = \overrightarrow{MB}.$
- B.
  $\overrightarrow{AB} = \overrightarrow{AC}.$
- C.
  $\overrightarrow{MN} = \overrightarrow{BC}.$
- D.
  $\left| \overrightarrow{BC} ight| = 2\left| \overrightarrow{MN} ight|.$
Ta có $MN$ là đường trung bình của tam giác $ABC$ .

Do đó $BC = 2MN\overset{}{ightarrow}\left| \overrightarrow{BC} ight| = 2\left| \overrightarrow{MN} ight|.$
Câu 10: Thông hiểu
Tính diện tích tam giác

Cho tam giác $ABC$ có $a = 4,b = 6,c = 8$ . Khi đó diện tích của tam giác là:
- A.
  $9\sqrt{15}.$
- B.
  $3\sqrt{15}.$
- C.
  $105.$
- D.
  $\frac{2}{3}\sqrt{15}.$
Ta có:

$p = \frac{a + b + c}{2} = \frac{4 + 6 + 8}{2} = 9.$

Suy ra: $S = \sqrt{p(p - a)(p - b)(p - c)} = 3\sqrt{15}.$
Câu 11: Vận dụng
Tính chiều cao của cột cờ

Để đo chiều cao từ mặt đất đến đỉnh cột cờ của một kỳ đài trước Ngọ Môn (Đại Nội – Huế), người ta cắm hai cọc AM và BN cao 1,5 mét so với mặt đất. Hai cọc này song song và cách nhau 10 mét và thẳng hàng so với tim cột cờ (Hình vẽ minh họa). Đặt giác kế tại đỉnh A và B để nhắm đến đỉnh cột cờ, người ta được các góc lần lượt là 51°40' và 45°39' so với đường song song mặt đất.
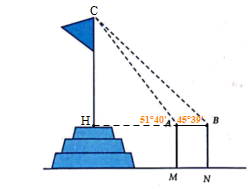
Chiều cao của cột cờ (làm tròn kết quả đến chữ số thập phân thứ hai) là:
- A.
  54,33 m
- B.
  54,63 m
- C.
  55,01 m
- D.
  56,88 m
Ta có: $\widehat {CAB} = {180^0} - {51^0}40' = {128^0}20'$
Xét tam giác ABC ta có:
$\begin{matrix} \widehat {ABC} + \widehat {CAB} + \widehat {ACB} = {180^0} \hfill \\ \Leftrightarrow \widehat {ACB} = {180^0} - \left( {\widehat {ABC} + \widehat {CAB}} ight) \hfill \\ \Leftrightarrow \widehat {ACB} = {180^0} - \left( {{{45}^0}39' + {{128}^0}20'} ight) \hfill \\ \Leftrightarrow \widehat {ACB} = {6^0}1\prime \hfill \\ \end{matrix}$
Áp dụng định lí sin trong tam giác ABC ta có:
$\begin{matrix} \dfrac{{AB}}{{\sin \widehat {ACB}}} = \dfrac{{AC}}{{\sin \widehat {ABC}}} = \dfrac{{BC}}{{\sin \widehat {CAB}}} \hfill \\ \Rightarrow \dfrac{{10}}{{\sin {6^0}1'}} = \dfrac{{AC}}{{\sin {{45}^0}39'}} \hfill \\ \Rightarrow AC = \dfrac{{10.\sin {{45}^0}39'}}{{\sin {6^0}1'}} \hfill \\ \end{matrix}$
Ta có tam giác ACH vuông tại C
$\begin{matrix} \Rightarrow CH = AC.\sin \widehat {HAC} \hfill \\ \Rightarrow CH = \dfrac{{10.\sin {{45}^0}39'}}{{\sin {6^0}1'}}.\sin {51^0}40' \approx 53,51\left( m ight) \hfill \\ \end{matrix}$
Chiều cao của cột cờ khoảng: $1,5+53,51=55,01(m)$
Câu 12: Nhận biết
Tìm khẳng định sai

Cho tam giác $ABC$ có trọng tâm $G$ và trung tuyến $AM$ . Khẳng định nào sau đây là sai?
- A.
  $\overrightarrow{GA} + 2\overrightarrow{GM} = \overrightarrow{0}$ .
- B.
  $\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} = 3\overrightarrow{OG}$ , với mọi điểm $O$ .
- C.
  $\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = \overrightarrow{0}$ .
- D.
  $\overrightarrow{AM} = - 2\overrightarrow{MG}$ .
Hình vẽ minh họa:

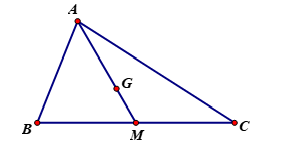
Ta có $AM = 3MG$

Mặt khác $\overrightarrow{AM}$ và $\overrightarrow{MG}$ ngược hướng

$\Rightarrow \overrightarrow{AM} = - 3\overrightarrow{MG}$ .
Câu 13: Nhận biết
Tính diện tích tam giác

Cho $\Delta ABC$ có $a = 4,c = 5,B = 150^{0}.$ Diện tích của tam giác là:
- A.
  $5\sqrt{3}.$
- B.
  $5.$
- C.
  $10.$
- D.
  $10\sqrt{3}\ .$
Ta có:

$S_{\Delta ABC} =\frac{1}{2}a.c.\sin B = \frac{1}{2}.4.5.\sin150^{0} = 5.$
Câu 14: Vận dụng
Chọn đáp án thích hợp

Cho tam giác đều $ABC$ cạnh $18cm$ . Tập hợp các điểm $M$ thỏa mãn đẳng thức $\left| 2\overrightarrow{MA} + 3\overrightarrow{MB} + 4\overrightarrow{MC} \right| = \left| \overrightarrow{MA} - \overrightarrow{MB} \right|$ là:
- A.
  Tập rỗng.
- B.
  Đường tròn cố định có bán kính $R = 2\ cm$ .
- C.
  Đường tròn cố định có bán kính $R = 3\ cm$ .
- D.
  Một đường thẳng.
Hình vẽ minh họa

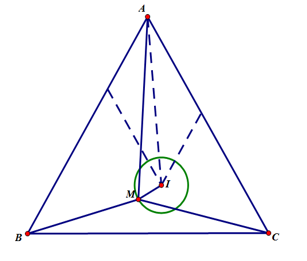
Ta có $\left| \overrightarrow{MA} - \overrightarrow{MB} \right| = \left| \overrightarrow{AB} \right| = 18$ .

Dựng điểm $I$ thỏa mãn $2\overrightarrow{IA} + 3\overrightarrow{IB} + 4\overrightarrow{IC} = \overrightarrow{0}$ $\Leftrightarrow \overrightarrow{AI} = \frac{1}{3}\overrightarrow{AB} + \frac{4}{9}\overrightarrow{AC}$ .

Khi đó:

$\left| 2\overrightarrow{MA} +3\overrightarrow{MB} + 4\overrightarrow{MC} \right| = \left|\overrightarrow{MA} - \overrightarrow{MB} \right|$

$\Leftrightarrow9\left| \overrightarrow{MI} \right| = 18 \Leftrightarrow IM =2$ .

Do đó tập hợp các điểm $M$ là đường tròn cố định có bán kính $R = 2\ cm$ .
Câu 15: Vận dụng
Tìm tọa độ điểm C

Trong hệ tọa độ $Oxy,$ cho tam giác $ABC$ có $A(1; - 1)$ , $B(5; - 3)$ và $C$ thuộc trục $Oy$ , trọng tâm $G$ của tam giác thuộc trục $Ox$ . Tìm tọa độ điểm $C.$
- A.
  $C(0;4)$
- B.
  $C(2;4)$
- C.
  $C(0;2)$
- D.
  $C(0; - 4)$
Vì $C$ thuộc trục $Oy\overset{}{ightarrow}$ $C$ có hoành độ bằng $0$ . Loại $C(2;4)$ .

Trọng tâm $G$ thuộc trục $Ox\overset{}{ightarrow}$ $G$ có tung độ bằng $0.$ Xét các đáp án còn lại chỉ có đáp án $C(0;4)$ thỏa mãn $\frac{y_{A} + y_{B} + y_{C}}{3} = 0.$
Câu 16: Thông hiểu

Xét tính đúng sai của các khẳng định

Cho hình chữ nhật $ABCD$ tâm I, $AB = 3,BC = 4$ . Xét tính đúng sai của các khẳng định sau?

a) $\overrightarrow{AD} = \overrightarrow{BC}$ . Đúng||Sai

b) $\overrightarrow{AB} + \overrightarrow{BD} = \overrightarrow{AD}$ . Đúng||Sai

c) $\overrightarrow{DC} + \overrightarrow{AD} = \overrightarrow{CA}$ . Sai||Đúng

d) $\left| \overrightarrow{CB} + \overrightarrow{CD} \right| = 5$ . Đúng||Sai

Đáp án là:

Cho hình chữ nhật $ABCD$ tâm I, $AB = 3,BC = 4$ . Xét tính đúng sai của các khẳng định sau?

a) $\overrightarrow{AD} = \overrightarrow{BC}$ . Đúng||Sai

b) $\overrightarrow{AB} + \overrightarrow{BD} = \overrightarrow{AD}$ . Đúng||Sai

c) $\overrightarrow{DC} + \overrightarrow{AD} = \overrightarrow{CA}$ . Sai||Đúng

d) $\left| \overrightarrow{CB} + \overrightarrow{CD} \right| = 5$ . Đúng||Sai

Tổng quan đáp án

a) Đúng

b) Đúng

c) Sai

d) Đúng

Hình vẽ minh họa

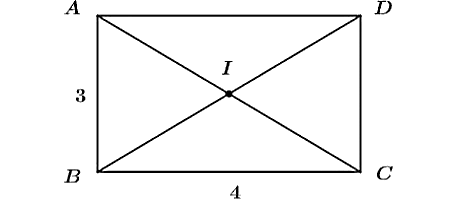
a) $\overrightarrow{AD} = \overrightarrow{BC}$ .

b) $\overrightarrow{AB} + \overrightarrow{BD} = \overrightarrow{AD}$ .

c) $\overrightarrow{DC} + \overrightarrow{AD} = \overrightarrow{AD} + \overrightarrow{DC} = \overrightarrow{AC}$ .

d) $\left| \overrightarrow{CB} + \overrightarrow{CD} \right| = \left| \overrightarrow{CA} \right| = CA = \sqrt{AB^{2} + BC^{2}} = \sqrt{3^{2} + 4^{2}} = 5$ .
Câu 17: Thông hiểu
Tính độ dài cạnh của tam giác

Tam giác $ABC$ có $a = 16,8$ ; $\widehat{B} = 56^{0}13'$ ; $\widehat{C} = 71^{0}$ . Cạnh $c$ bằng bao nhiêu?
- A.
  $29,9.$
- B.
  $14,1.$
- C.
  $17,5.$
- D.
  $19,9.$
Trong tam giác $ABC$ : $\widehat{A} + \widehat{B} + \widehat{C} = 180^{0}$

$\Rightarrow \widehat{A} = 180^{0} - 71^{0} - 56^{0}13' = 52^{0}47'$ .

Mặt khác $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

$\Rightarrow \frac{a}{\sin A} = \frac{c}{\sin C}$

$\Rightarrow c = \frac{a.\sin C}{\sin A} =\frac{16,8.sin71^{0}}{\sin52^{0}47'} \simeq 19,9\ .$
Câu 18: Thông hiểu
Thực hiện phép tính

Cho tam giác đều $ABC$ cạnh $a$ . Khi đó $\left| \overrightarrow{AB} - \overrightarrow{CA} \right| =$
- A.
  $a\sqrt{3}$ .
- B.
  $\frac{a\sqrt{3}}{2}$ .
- C.
  $2a$ .
- D.
  $a$ .
Gọi $I$ là trung điểm $BC$ .

Ta có:

$\left| \overrightarrow{AB} - \overrightarrow{CA} \right| = \left| \overrightarrow{AB} + \overrightarrow{AC} \right| = 2\left| \overrightarrow{AM} \right| = 2.\frac{a\sqrt{3}}{2} = a\sqrt{3}$ .
Câu 19: Nhận biết
Tính diện tích tam giác

Cho $\Delta ABC$ có $a = 6,b = 8,c = 10.$ Diện tích $S$ của tam giác trên là:
- A.
  $48.$
- B.
  $24.$
- C.
  $12.$
- D.
  $30.$
Ta có: Nửa chu vi $\Delta ABC$ : $p = \frac{a + b + c}{2}$ .

Áp dụng công thức Hê-rông: $S = \sqrt{p(p - a)(p - b)(p - c)}$ $= \sqrt{12(12 - 6)(12 - 8)(12 - 10)}$ $= 24$ .
Câu 20: Nhận biết
Chọn câu đúng

Cho tam giác $ABC$ . Lấy điểm $M$ trên $BC$ sao cho $\overrightarrow{AB}.\overrightarrow{AM} - \overrightarrow{AC}.\overrightarrow{AM} = 0$ . Câu nào sau đây đúng
- A.
  $M$ là trung điểm của $BC$ .
- B.
  $AM$ là đường phân giác của góc $A$ .
- C.
  $AM\bot BC$ .
- D.
  $\left( \overrightarrow{AM};\overrightarrow{BC} \right) = 60^{0}$ .
Ta có:

$\overrightarrow{AB}.\overrightarrow{AM} -\overrightarrow{AC}.\overrightarrow{AM} = 0$

$\Leftrightarrow\overrightarrow{AM}\left( \overrightarrow{AB} - \overrightarrow{AC}\right) = 0$ $\Leftrightarrow \overrightarrow{AM}.\overrightarrow{CB} =0$ nên $AM\bot BC$ .
Câu 21: Thông hiểu
Tìm cặp vectơ cùng hướng

Gọi $M,\ \ N$ lần lượt là trung điểm của các cạnh $AB,\ \ AC$ của tam giác đều $ABC$ . Hỏi cặp vectơ nào sau đây cùng hướng?
- A.
  $\overrightarrow{MN}$ và $\overrightarrow{CB}.$
- B.
  $\overrightarrow{AB}$ và $\overrightarrow{MB}.$
- C.
  $\overrightarrow{MA}$ và $\overrightarrow{MB}.$
- D.
  $\overrightarrow{AN}$ và $\overrightarrow{CA}.$
Cặp vectơ nào sau đây cùng hướng là: $\overrightarrow{AB}$ và $\overrightarrow{MB}.$
Câu 22: Thông hiểu
Tính độ dài cạnh BC.

Tam giác ABC có $AB=\sqrt{2},AC=\sqrt{3}$ và $\widehat{C}=45°$ . Tính độ dài cạnh BC.
- A.
  $BC=\sqrt{5}$
- B.
  $BC=\frac{\sqrt{6}+\sqrt{2}}{2}$
- C.
  $BC=\frac{\sqrt{6}+\sqrt{3}}{2}$
- D.
  $BC=\sqrt{6}$
Áp dụng định lý côsin: $A{B^2} = C{A^2} + C{B^2} - 2CA.CB.\cos 45^\circ$ $\Leftrightarrow 2 = 3 + C{B^2} - 2\sqrt 3 .CB.\frac{{\sqrt 2 }}{2}$ $\Leftrightarrow C{B^2} - \sqrt 6 CB + 1 = 0$ $\Rightarrow BC=\frac{{\sqrt 6 + \sqrt 2 }}{2}$ .
Câu 23: Vận dụng cao
Tính bán kính của đường tròn

Cho hình vuông $ABCD$ tâm $O$ cạnh a. Biết rằng tập hợp điểm $M$ thỏa mãn $2MA^{2} + MB^{2} + 2MC^{2} + MD^{2} = 9a^{2}$ là một đường tròn. Tính bán kính của đường tròn.
- A.
  $R = \frac{a}{2}$
- B.
  $R = a\sqrt{3}$
- C.
  $R = a$
- D.
  $R = 2a$
Ta có:

$2MA^{2} + MB^{2} + 2MC^{2} + MD^{2} = 9a^{2}$

$\Leftrightarrow 2\left( \overrightarrow{MO} + \overrightarrow{OA} ight)^{2} + \left( \overrightarrow{MO} + \overrightarrow{OB} ight)^{2} + 2\left( \overrightarrow{MO} + \overrightarrow{OC} ight)^{2} + \left( \overrightarrow{MO} + \overrightarrow{OD} ight)^{2} = 9a^{2}$

$\Leftrightarrow 6MO^{2} + 2OA^{2} + OB^{2} + 2OC^{2} + OD^{2}$

$+ 2\overrightarrow{MO}\left( 2\overrightarrow{OA} + \overrightarrow{OB} + 2\overrightarrow{OC} + \overrightarrow{OD} ight) = 9a^{2}$

Do $2\overrightarrow{OA} + \overrightarrow{OB} + 2\overrightarrow{OC} + \overrightarrow{OD} = \overrightarrow{0}$

$\Leftrightarrow 6MO^{2} + 3a^{2} = 9a^{2}$

$\Leftrightarrow MO = a$

Vậy tập hợp các điểm $M$ là đường tròn tâm $O$ , bán kính $R = a$ .
Câu 24: Nhận biết
Tính góc giữa hai vectơ

Cho hai vecto $\overrightarrow{a},\overrightarrow{b}eq \overrightarrow{0}$ . Xác định góc giữa hai vecto $\overrightarrow{a}$ và $\overrightarrow{b}$ khi $\overrightarrow{a}\times \overrightarrow{b}=-|\overrightarrow{a}|\times |\overrightarrow{b}|$
- A.
  $180^{\circ}$
- B.
  $0^{\circ}$
- C.
  $90^{\circ}$
- D.
  $45^{\circ}$
Ta có:
$\begin{matrix} \vec a \times \vec b = - |\vec a|.|\vec b| = |\vec a|.|\vec b|.\cos {180^0} \hfill \\ \Rightarrow \left( {\vec a,\vec b} ight) = {180^0} \hfill \\ \end{matrix}$
Câu 25: Thông hiểu
Tính độ dài vectơ

Cho tam giác $ABC$ đều cạnh $a$ . Khi đó $\left| \overrightarrow{AB} + \overrightarrow{AC} \right|$ bằng:
- A.
  $\left| \overrightarrow{AB} + \overrightarrow{AC} \right| = a\sqrt{3}.$
- B.
  $\left| \overrightarrow{AB} + \overrightarrow{AC} \right| = \frac{a\sqrt{3}}{2}.$
- C.
  $\left| \overrightarrow{AB} + \overrightarrow{AC} \right| = 2a.$
- D.
  $\left| \overrightarrow{AB} +\overrightarrow{AC} \right| =a\sqrt{2}$
Hình vẽ minh họa

Gọi $H$ là trung điểm của $BC \Rightarrow AH\bot BC.$

Suy ra $AH = \frac{BC\sqrt{3}}{2} = \frac{a\sqrt{3}}{2}.$

Ta lại có $\left| \overrightarrow{AB} + \overrightarrow{AC} \right| = \left| 2\overrightarrow{AH} \right| = 2.\frac{a\sqrt{3}}{2} = a\sqrt{3}$ .
Câu 26: Thông hiểu
Tính độ lớn góc

Trong mặt phẳng $Oxy$ cho $A(1;2),\ \ B(4;1),\ \ C(5;4)$ . Tính $\widehat{BAC}$ ?
- A.
  $60^{o}$ .
- B.
  $45^{o}$ .
- C.
  $90^{o}$ .
- D.
  $120^{o}$ .
Ta có $\overrightarrow{AB} = (3; - 1)$ , $\overrightarrow{AC} = (4;2)$ suy ra $\cos\left( \overrightarrow{AB};\overrightarrow{AC} ight) = \frac{\overrightarrow{AB}.\overrightarrow{AC}}{AB.AC} = \frac{10}{\sqrt{10}.\sqrt{20}} = \frac{\sqrt{2}}{2} \Rightarrow \left( \overrightarrow{AB};\overrightarrow{AC} ight) = 45^{o}$ .
Câu 27: Thông hiểu
Tìm giá trị m, n thỏa mãn đẳng thức

Gọi $G$ là trọng tâm tam giác $ABC$ . Đặt $\overrightarrow{GA} = \overrightarrow{a},\overrightarrow{GB} = \overrightarrow{b}$ . Hãy tìm $m,n$ để có $\overrightarrow{BC} = m\overrightarrow{a} + n\overrightarrow{b}.$
- A.
  $m = 1,n = 2.$
- B.
  $m = - 1,n = - 2.$
- C.
  $m = 2,n = 1.$
- D.
  $m = - 2,n = - 1.$
Ta có $\overrightarrow{BC} = \overrightarrow{BG} + \overrightarrow{GC} = \overrightarrow{BG} - \left( \overrightarrow{GA} + \overrightarrow{GB} \right)$ $= - \overrightarrow{GA} - 2\overrightarrow{GB}$ do $\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = 0$
Câu 28: Nhận biết
Chọn câu đúng

Cho tam giác $ABC$ , gọi $M$ là trung điểm của $BC$ và $G$ là trọng tâm của tam giác $ABC$ . Câu nào sau đây đúng?
- A.
  $\overrightarrow{GB} + \overrightarrow{GC} = 2\overrightarrow{GM}$ .
- B.
  $\overrightarrow{GB} + \overrightarrow{GC} = 2\overrightarrow{GA}$ .
- C.
  $\overrightarrow{AB} + \overrightarrow{AC} = 2\overrightarrow{AG}$ .
- D.
  $\overrightarrow{AB} + \overrightarrow{AC} = 3\overrightarrow{AM}$ .
Hình vẽ minh họa:

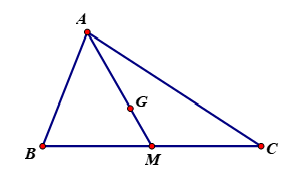
Do $M$ là trung điểm của $BC$ nên ta có: $\overrightarrow{GB} + \overrightarrow{GC} = 2\overrightarrow{GM}$ .
Câu 29: Vận dụng
Tính giá trị biểu thức

Cho góc α với $\cosα=-\frac{\sqrt{3}}{2}$ . Giá trị của biểu thức: $A = \sin 2\alpha - 3\tan \alpha + \cot 3\alpha$ là:
- A.
  $\frac{1}{4}-4\sqrt{3}$
- B.
  $\frac{1}{2}-2\sqrt{3}$
- C.
  $\frac{1}{4}-2\sqrt{3}$
- D.
  $\frac{1}{2}-4\sqrt{3}$
Ta có:
$\cosα=-\frac{\sqrt{3}}{2}$
=> $\alpha = {150^0}$
$\begin{matrix} \Rightarrow A = \sin {2.150^0} - 3\tan {150^0} + \cot {3.150^0} \hfill \\ A = \dfrac{1}{4} - 2\sqrt 3 \hfill \\ \end{matrix}$
Câu 30: Vận dụng cao
Xác định số phương trình luôn có nghiệm với mọi giá trị m

Xác định số phương trình luôn có nghiệm với mọi giá trị của tham số m trong các phương trình dưới đây?

$\left| \sin x ight| = \frac{m}{m^{2} + 1}\ \ (i)$

$\sin x = \frac{2m}{m^{2} + 1}\ \ (ii)$

$\tan x = \frac{2m}{m^{2} + 1}\ \ (iii)$

$\sin x = \frac{|m|}{m^{2} + 1}\ \ (iv)$
- A.
  $1$
- B.
  $2$
- C.
  $3$
- D.
  $4$
Với $m < 0$ thì $(i)$ vô nghiệm.

Vì với mọi giá trị thực của m ta có: $m^{2} - 2|m| + 1 \geq 0$ nên $m^{2} + 1 \geq 2|m| \geq |m|$

Từ đó suy ra $\left\{ \begin{matrix}- 1 \leq \dfrac{2m}{m^{2} + 1} \leq 1 \\0 \leq \dfrac{|m|}{m^{2} + 1} \leq 1 \\\end{matrix} ight.$ vậy phương trình $(ii),(iv)$ luôn có nghiệm.

Phương trình $(iii)$ luôn có nghiệm với mọi giá trị thực của m.
Câu 31: Vận dụng
Mệnh đề nào sau đây sai?

Mệnh đề nào sau đây sai?
- A.
  Nếu $M$ là trung điểm đoạn thẳng $AB$ thì $\overrightarrow{MA} + \overrightarrow{MB} = \overrightarrow{0}.$
- B.
  Nếu $G$ là trọng tâm tam giác $ABC$ thì $\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = \overrightarrow{0}.$
- C.
  Nếu $ABCD$ là hình bình hành thì $\overrightarrow{CB} + \overrightarrow{CD} = \overrightarrow{CA}.$
- D.
  Nếu ba điểm phân biệt $A,\ \ B,\ \ C$ nằm tùy ý trên một đường thẳng thì $\left| \overrightarrow{AB} ight| + \left| \overrightarrow{BC} ight| = \left| \overrightarrow{AC} ight|.$
Với ba điểm phân biệt $A,\ \ B,\ \ C$ nằm trên một đường thẳng, đẳng thức $\left| \overrightarrow{AB} ight| + \left| \overrightarrow{BC} ight| = \left| \overrightarrow{AC} ight| \Leftrightarrow AB + BC = AC$ xảy ra khi $B$ nằm giữa $A$ và $C$ .

Chọn đáp án sai là: Nếu ba điểm phân biệt $A,B,C$ nằm tùy ý trên một đường thẳng thì $\left| \overrightarrow{AB} ight| + \left|\overrightarrow{BC} ight| = \left| \overrightarrow{AC}ight|.$
Câu 32: Nhận biết
Tính độ dài tổng hai vectơ

Cho hình chữ nhật $ABCD$ biết $AB = 4a$ và $AD = 3a$ thì độ dài $\overrightarrow{AB} + \overrightarrow{AD}$ bằng bao nhiêu?
- A.
  $7a$ .
- B.
  $6a$ .
- C.
  $2a\sqrt{3}$ .
- D.
  $5a$ .
Ta có: $\left| \overrightarrow{AB} + \overrightarrow{AD} \right| = \left| \overrightarrow{AC} \right| = AC = 5a$
Câu 33: Thông hiểu

Xét tính đúng sai của các khẳng định

Trong mặt phẳng tọa độ $Oxy,$ cho tam giác $ABC$ có $A( - 3;0)$ , $B(3;0)$ và $C(2;6).$

a) Tích vô hướng của hai véc tơ là một số. Đúng||Sai

b) $\overrightarrow{AB}.\overrightarrow{BC} = 8$ . Sai||Đúng

c) $AB$ vuông góc với trục $Ox$ . Đúng||Sai

d) Gọi $H(a;b)$ là trực tâm của tam giác đã cho. Tính được giá trị biểu thức $a - 6b = 2$ . Sai||Đúng

Đáp án là:

Trong mặt phẳng tọa độ $Oxy,$ cho tam giác $ABC$ có $A( - 3;0)$ , $B(3;0)$ và $C(2;6).$

a) Tích vô hướng của hai véc tơ là một số. Đúng||Sai

b) $\overrightarrow{AB}.\overrightarrow{BC} = 8$ . Sai||Đúng

c) $AB$ vuông góc với trục $Ox$ . Đúng||Sai

d) Gọi $H(a;b)$ là trực tâm của tam giác đã cho. Tính được giá trị biểu thức $a - 6b = 2$ . Sai||Đúng

a) Đúng

b) Sai

c) Đúng

d) Sai

a) Tích vô hướng của hai vectơ là một số.

b) Ta có: $\overrightarrow{AB} = (6;0);\overrightarrow{BC} = ( - 1;6)$ $\Rightarrow \overrightarrow{AB}.\overrightarrow{BC} = - 6 + 0 = - 6$

c) $\overrightarrow{AB} = (6;0);\overrightarrow{i} = (0;1)\ \Rightarrow \ \ \overrightarrow{AB}.\overrightarrow{i} = 0 \Rightarrow \overrightarrow{AB}\bot\overrightarrow{i}$ .

Vậy $AB$ vuông góc với trục $Ox$ .

d) Gọi $H(a;b)$ là trực tâm của tam giác đã cho.

Ta có:

$\overrightarrow{AH} = (a + 3\ ;\ b)\ ,\ \overrightarrow{BC} = ( - 1\ ;\ 6)\ ,\ \overrightarrow{BH} = (a - 3\ ;\ b)\ ,\ \overrightarrow{AC} = (5\ ;\ 6)$

Vì $H$ là trực tâm tam giác $ABC$ nên:

$\left\{ \begin{matrix} AH\bot BC \\ BH\bot AC \end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix} \overrightarrow{AH}.\overrightarrow{BC} = 0 \\ \overrightarrow{BH}.\overrightarrow{AC} = 0 \end{matrix} \right.$

$\Leftrightarrow \left\{ \begin{matrix}- a - 3 + 6b = 0 \\5a - 15 + 6b = 0\end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix} - a + 6b = 3 \\ 5a + 6b = 15 \end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix} a = 2 \\ b = \frac{5}{6} \end{matrix} \right.$

Suy ra $a - 6b = - 3$ .
Câu 34: Nhận biết
Chọn mệnh đề đúng

Cho bốn điểm $A,\ \ B,\ \ C,\ \ D$ . Mệnh đề nào sau đây đúng?
- A.
  $\overrightarrow{AB} + \overrightarrow{CD} = \overrightarrow{AD} + \overrightarrow{CB}.$
- B.
  $\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CD} = \overrightarrow{DA}.$
- C.
  $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{CD} + \overrightarrow{DA}.$
- D.
  $\overrightarrow{AB} + \overrightarrow{AD} = \overrightarrow{CD} + \overrightarrow{CB}.$
Ta có: $\overrightarrow{AB} + \overrightarrow{CD} = \overrightarrow{AD} + \overrightarrow{DB} + \overrightarrow{CB} + \overrightarrow{BD} = \overrightarrow{AD} + \overrightarrow{CB}$ .
Câu 35: Vận dụng cao
Tam giác ABC là tam giác gì

Cho tam giác $ABC$ thỏa mãn biểu thức

$\sin\dfrac{\widehat{B}}{2}.\cos^{3}\dfrac{\widehat{C}}{2}= \sin\frac{\widehat{C}}{2}.\cos^{3}\dfrac{\widehat{B}}{2}$

Khi đó tam giác $ABC$ là tam giác gì?
- A.
  Tam giác cân tại A
- B.
  Tam giác đều
- C.
  Tam giác vuông tại B
- D.
  Tam giác vuông cân C
Ta có:

$\sin\dfrac{\widehat{B}}{2}.\cos^{3}\dfrac{\widehat{C}}{2}= \sin\dfrac{\widehat{C}}{2}.\cos^{3}\dfrac{\widehat{B}}{2}$

$\Leftrightarrow\tan\dfrac{\widehat{B}}{2}.\dfrac{1}{\cos^{2}\dfrac{\widehat{B}}{2}} =\tan\dfrac{\widehat{C}}{2}.\dfrac{1}{\cos^{2}\dfrac{\widehat{C}}{2}}$

$\Leftrightarrow\tan\dfrac{\widehat{B}}{2}.\left( 1 + \tan^{2}\dfrac{\widehat{B}}{2}ight) = \tan\dfrac{\widehat{C}}{2}.\left( 1 +\tan^{2}\dfrac{\widehat{C}}{2} ight)$

Đặt $\tan\dfrac{\widehat{B}}{2} =x;\tan\dfrac{\widehat{C}}{2} = y$ khi đó ta có:

$x\left( 1 + x^{2} ight) = y\left( 1 + y^{2} ight)$

$\Leftrightarrow x^{3} - y^{3} + x - y = 0$

$\Leftrightarrow (x - y)\left( x^{2} + xy + y^{2} + 1 ight) = 0$

$\Leftrightarrow x - y = 0$

Do đó $\tan\frac{\widehat{B}}{2} = \tan\frac{\widehat{C}}{2} \Leftrightarrow \frac{\widehat{B}}{2} = \frac{\widehat{C}}{2} \Leftrightarrow \widehat{B} = \widehat{C}$

Vậy tam giác ABC là tam giác cân tại A.
Câu 36: Thông hiểu
Chọn đẳng thức đúng

Cho 6 điểm $A,B,C,D,E,F$ . Đẳng thức nào sau đây đúng.
- A.
  $\overrightarrow{AB} + \overrightarrow{CD} + \overrightarrow{FA} + \overrightarrow{BC} + \overrightarrow{EF} + \overrightarrow{DE} = \overrightarrow{0}$ .
- B.
  $\overrightarrow{AB} + \overrightarrow{CD} + \overrightarrow{FA} + \overrightarrow{BC} + \overrightarrow{EF} + \overrightarrow{DE} = \overrightarrow{AF}$ .
- C.
  $\overrightarrow{AB} + \overrightarrow{CD} + \overrightarrow{FA} + \overrightarrow{BC} + \overrightarrow{EF} + \overrightarrow{DE} = \overrightarrow{AE}$ .
- D.
  $\overrightarrow{AB} + \overrightarrow{CD} + \overrightarrow{FA} + \overrightarrow{BC} + \overrightarrow{EF} + \overrightarrow{DE} = \overrightarrow{AD}$ .
Ta có:

$\overrightarrow{AB} + \overrightarrow{CD} + \overrightarrow{FA} + \overrightarrow{BC} + \overrightarrow{EF} + \overrightarrow{DE}$

$= \overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CD} + \overrightarrow{DE} + \overrightarrow{EF} + \overrightarrow{FA} = \overrightarrow{0}$
Câu 37: Nhận biết
Chọn đáp án đúng

Trong các hệ thức sau hệ thức nào đúng?
- A.
  $sin2\alpha + cos2\alpha = 1$ .
- B.
  $\sin\alpha^{2} + \cos\alpha^{2} = 1$ .
- C.
  $sin^{2}\alpha + \cos\alpha^{2} = 1$ .
- D.
  $sin^{2}\alpha + cos^{2}\alpha = 1$ .
Công thức lượng giác cơ bản ta có hệ thức đúng là: $sin^{2}\alpha + cos^{2}\alpha = 1$ .
Câu 38: Vận dụng cao
Tìm điều kiện của x và y

Cho hình bình hành $ABCD$ . Lấy hai điểm $M,N$ sao cho $\overrightarrow{CM} = \frac{1}{2}\overrightarrow{CB};\overrightarrow{CN} = \frac{1}{3}\overrightarrow{CD}$ , lấy tiếp hai điểm $I,J$ sao cho $\overrightarrow{CI} = x\overrightarrow{CD};\overrightarrow{BJ} = y\overrightarrow{BI}$ . Để $J$ là trọng tâm tam giác $AMN$ thì $x,y$ thỏa mãn điều kiện nào sau đây:
- A.
  $x = \frac{3}{4};y = \frac{1}{2}$
- B.
  $x = \frac{8}{9};y = \frac{1}{2}$
- C.
  $x = \frac{1}{9};y = 1$
- D.
  $x = \frac{1}{4};y = \frac{3}{2}$
Hình vẽ minh họa

$\overrightarrow{JA} + \overrightarrow{JM} + \overrightarrow{JN} = \overrightarrow{BA} - \overrightarrow{BJ} + \overrightarrow{JB} + \overrightarrow{BM} + \overrightarrow{JI} + \overrightarrow{IN}$

$= \overrightarrow{BA} - 2\overrightarrow{BJ} + \frac{\overrightarrow{BC}}{2} + \overrightarrow{BI} - \overrightarrow{BJ} + \overrightarrow{CN} - \overrightarrow{CI}$

$= \overrightarrow{BA} + \frac{\overrightarrow{BC}}{2} + ( - 3y + 1).\overrightarrow{BI} + \overrightarrow{CN} - \overrightarrow{CI}$

$= \overrightarrow{BA} + \frac{\overrightarrow{BC}}{2} + ( - 3y + 1).\left( \overrightarrow{BC} + \overrightarrow{CI} ight) + \overrightarrow{CN} - \overrightarrow{CI}$

$= \overrightarrow{BA} + \left( \frac{3}{2} - 3y ight)\left( \overrightarrow{AC} - \overrightarrow{AB} ight) + \overrightarrow{CN} - 3y.\overrightarrow{CI}$

$= \overrightarrow{BA} + \left( \frac{3}{2} - 3y ight)\left( \overrightarrow{AC} - \overrightarrow{AB} ight) + \frac{1}{3}\overrightarrow{CD} - 3xy.\overrightarrow{CD}$

$= \overrightarrow{BA} + \left( \frac{3}{2} - 3y ight)\left( \overrightarrow{AC} - \overrightarrow{AB} ight) + \left( \frac{1}{3} - 3xy ight).\overrightarrow{BA}$

$= \left( - \frac{17}{6} + 3y + 3xy ight).\overrightarrow{AB} + \left( \frac{3}{2} - 3y ight).\overrightarrow{AC}$

Để J là trọng tâm tam giác AMN thì

$\overrightarrow{JA} + \overrightarrow{JM} + \overrightarrow{JN} = \overrightarrow{0}$

$\Leftrightarrow \left( - \frac{17}{6} + 3y + 3xy ight).\overrightarrow{AB} + \left( \frac{3}{2} - 3y ight).\overrightarrow{AC} = \overrightarrow{0}$

Mặt khác do $\overrightarrow{AB};\overrightarrow{AC}$ không cùng phương nên ta suy ra:

$\left\{ \begin{matrix}- \dfrac{17}{6} + 3y + 3xy = 0 \\\dfrac{3}{2} - 3y = 0 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x = \dfrac{8}{9} \\y = \dfrac{1}{2} \\\end{matrix} ight.$

Vậy với $x = \frac{8}{9};y = \frac{1}{2}$ thì điểm J là trọng tâm tam giác AMN.
Câu 39: Thông hiểu
Chọn khẳng định đúng

Tam giác đều ABC có đường cao AH. Khẳng định nào sau đây là đúng?
- A.
  $\cos\widehat{BAH}=\frac{1}{\sqrt{3}}$
- B.
  $\cos\widehat{ABC}=\frac{\sqrt{3}}{2}$
- C.
  $\cos\widehat{AHC}=\frac{1}{2}$
- D.
  $\cos\widehat{BAH}=\frac{\sqrt{3}}{2}$
Hình ảnh minh họa
Do tam giác ABC là tam giác đều có AH là đường cao nên đồng thời là đường phân giác
=> $\widehat {BAH} = \frac{1}{2}\widehat {BAC}=30^0;\widehat {ABC} = {60^0};\widehat {AHC} = {90^0}$
Do đó: $\sin \widehat {BAH} = \frac{1}{2};\sin \widehat {BAH} = \frac{{\sqrt 3 }}{2}$
Ta có: $\widehat {ABC} = {60^0} \Rightarrow \sin \widehat {ABC} = \frac{{\sqrt 3 }}{2}$
Câu 40: Nhận biết
Tính giá trị biểu thức

Giá trị của $\cos30^{0} +\sin60^{0}$ bằng bao nhiêu?
- A.
  $\frac{\sqrt{3}}{3}$ .
- B.
  $\frac{\sqrt{3}}{2}$ .
- C.
  $\sqrt{3}$ .
- D.
  $1$ .
Ta có: $\cos30^{0} + \sin60^{0} =\frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{2} = \sqrt{3}$ .

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Chương 4 Hệ thức lượng trong tam giác. Vectơ Kết quả

Thời gian làm bài: 00:00:00
Số câu đã làm: 0
Điểm tạm tính: 0
Điểm thưởng: 0
Tài khoản làm: Đăng nhập

Làm lại

Chia sẻ bởi:
Khang Anh

31 Bài viết đã được lưu

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Số điện thoại này đã được xác thực!

Bạn có thể dùng Sđt này đăng nhập tại đây!

Lỗi gửi SMS, liên hệ Admin

Sắp xếp theo

Xóa Đăng nhập để Gửi

Đề kiểm tra 45 phút Chương 4 Hệ thức lượng trong tam giác. Vectơ

Thời gian còn lại 45:00 Số câu đã làm 0/40

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

Chưa làm Đã làm

Làm lại Nộp bài

Tìm bài trong mục này

Chương 1: Mệnh đề toán học. Tập hợp
Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
Chương 3: Hàm số và đồ thị
Chương 4: Hệ thức lượng trong tam giác. Vectơ
Đề thi học kì 1
Chương 5: Đại số tổ hợp
Đề thi giữa học kì 2
Chương 6: Một số yếu tố thống kê và xác suất
Chương 7: Phương pháp tọa độ trong mặt phẳng
Đề thi học kì 2

Lớp 10
Khóa học Lớp 10
Toán 10 - Cánh diều

Toán 10 - Cánh diều

Đề thi học kì 2 Toán lớp 10 Cánh Diều - Đề 4
Đề thi giữa học kì 2 Toán 10 Cánh Diều (Đề 5)
Đề thi học kì 2 Toán lớp 10 Cánh Diều - Đề 1
Đề thi học kì 2 Toán lớp 10 Cánh Diều - Đề 5
Đề thi học kì 2 Toán lớp 10 Cánh Diều - Đề 3
Đề thi học kì 2 Toán lớp 10 Cánh Diều - Đề 2

Xem thêm

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Đề kiểm tra 45 phút Chương 4 Hệ thức lượng trong tam giác. Vectơ

Chúc mừng Bạn đã hoàn thành bài!

Toán 10 - Cánh diều

Đề thi học kì 2 Toán lớp 10 Cánh Diều - Đề 4

Đề thi giữa học kì 2 Toán 10 Cánh Diều (Đề 5)

Đề thi học kì 2 Toán lớp 10 Cánh Diều - Đề 1

Đề thi học kì 2 Toán lớp 10 Cánh Diều - Đề 5

Đề thi học kì 2 Toán lớp 10 Cánh Diều - Đề 3

Đề thi học kì 2 Toán lớp 10 Cánh Diều - Đề 2