Tích vô hướng của hai vectơ
- Cho hai vectơ
\(\overrightarrow u\) và \(\overrightarrow v\) khác \(\overrightarrow 0\). Đặt \(\overrightarrow {AB} = \overrightarrow u;\overrightarrow {AC}=\overrightarrow v .\) - Khi đó, góc giữa hai vectơ \(\overrightarrow u\) và \(\overrightarrow v\) chính là góc \(\widehat {BAC}\).
- Kí hiệu: \((\overrightarrow u;\overrightarrow v)=\widehat {BAC} .\)
Chú ý:
- Nếu \((\overrightarrow u;\overrightarrow v)=90^{\circ}\) thì ta nói hai vectơ này vuông góc với nhau. Kí hiệu: \(\overrightarrow u\perp \overrightarrow v .\)
- Vectơ \(\overrightarrow 0\) vuông góc với mọi vectơ.
2. Tích vô hướng của hai vectơ
Tích vô hướng của hai vectơ \(\overrightarrow u\) và \(\overrightarrow v\) là một số, kí hiệu là \(\overrightarrow u.\overrightarrow v\), được xác định bởi công thức:
\(\overrightarrow u.\overrightarrow v=|\overrightarrow u|.|\overrightarrow v|.\cos (\overrightarrow u;\overrightarrow v)\)
Chú ý:
- \(\overrightarrow u\perp \overrightarrow v \Leftrightarrow \overrightarrow u.\overrightarrow v=0 .\)
- \(\overrightarrow u.\overrightarrow u\) còn được viết là \(\overrightarrow {u}^2\), còn gọi là bình phương vô hướng của vectơ \(\overrightarrow u\). Ta có: \(\overrightarrow u^2=|\overrightarrow u|^2 .\)
Tính chất của tích vô hướng:
Với ba vectơ \(\overrightarrow u,\overrightarrow v,\overrightarrow w\) và mọi số thực \(k\), ta có:
- \(\overrightarrow u.\overrightarrow v=\overrightarrow v.\overrightarrow u\)
- \(\overrightarrow u(\overrightarrow v+\overrightarrow w)=\overrightarrow u.\overrightarrow v+\overrightarrow u.\overrightarrow w\)
- \((k\overrightarrow u).\overrightarrow v=k(\overrightarrow u.\overrightarrow v)=\overrightarrow u.(k\overrightarrow v)\)
Ví dụ 1: Cho tam giác đều \(ABC\) cạnh bằng \(1\). Tính tích vô hướng \(\overrightarrow {AB}.\overrightarrow {AC}\) và \(\overrightarrow {AB}. \overrightarrow {BC}\).
Hướng dẫn giải
Nhận xét: Góc giữa hai vectơ \(\overrightarrow {AB}\) và \(\overrightarrow {AC}\) là góc \(\widehat {BAC}=60^{\circ}\).
Ta có: \(\overrightarrow {AB}.\overrightarrow {AC}=AB.AC.\cos A =1.1.\cos 60^{\circ} =\frac12 .\)
Nhận xét: Góc giữa hai vectơ \(\overrightarrow {AB}\) và \(\overrightarrow {BC}\) là góc \(120^{\circ}\).
Ta có: \(\overrightarrow {AB}. \overrightarrow {BC}=AB.BC.\cos 120^{\circ} =-\frac12 .\)
Ví dụ 2: Cho hình vuông \(ABCD\) cạnh bằng \(a\) và có tâm \(O\). Tính các tích vô hướng:
a) \(\overrightarrow {AC}.\overrightarrow {AB}\)
b) \(\overrightarrow {OA}.\overrightarrow {CB}\)
Hướng dẫn giải
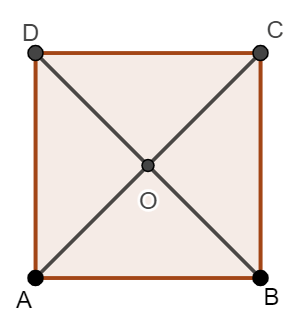
Hình vuông cạnh bằng \(a\) nên đường chéo \(CA=a\sqrt2\) (Pytago trong tam giác \(CAB\)).
Do đó \(CO=\frac 12CA=\frac {a\sqrt2}2\).
a) Ta có: \(\overrightarrow {AC}.\overrightarrow {AB} =AC.AB.\cos \widehat{BAC}\)\(=a\sqrt2.a.\cos45^{\circ} =a^2\).
b) Ta có: \(\overrightarrow {OA}.\overrightarrow {CB} =\overrightarrow {CO}.\overrightarrow {CB}=CO.CB.\cos \widehat{BOC}\)\(=\frac {a\sqrt2}2.a.\cos 45^{\circ} =\frac{a^2}2\).
Ví dụ 3: Cho tam giác \(ABC\) và đường cao \(AH\). Chứng minh rằng:
a) \(\overrightarrow{BA}.\overrightarrow{AH}=\overrightarrow{CA}.\overrightarrow{AH}\)
b) \(\overrightarrow{AC}.\overrightarrow{CB}=\overrightarrow{HC}.\overrightarrow{CB}\)
Hướng dẫn giải
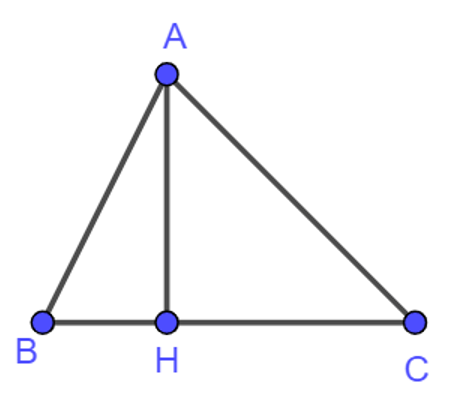
a) Ta có: \(\overrightarrow{BA}.\overrightarrow{AH}=(\overrightarrow{BC}+\overrightarrow{CA}).\overrightarrow{AH}\)\(=\overrightarrow{BC}.\overrightarrow{AH}+\overrightarrow{CA}.\overrightarrow{AH} =\overrightarrow{CA}.\overrightarrow{AH}\) do \(\overrightarrow {BC}.\overrightarrow {AH}=0\) vì \(BC\perp AH\).
b) Ta có: \(\overrightarrow{AC}.\overrightarrow{CB}=(\overrightarrow{AH}+\overrightarrow{HC}).\overrightarrow{CB}\)\(=\overrightarrow{AH}.\overrightarrow{CB}+\overrightarrow{HC}.\overrightarrow{CB}=\overrightarrow{HC}.\overrightarrow{CB}\) do \(\overrightarrow{AH}.\overrightarrow{CB}=0\) vì \(AH \perp CB\).
