Khái niệm vectơ
- Là một đoạn thẳng có hướng, nghĩa là trong hai điểm mút của đoạn thẳng, đã chỉ rõ điểm đầu và điểm cuối.
- Kí hiệu: Nếu vectơ có điểm đầu là
\(A\), điểm cuối là \(B\) thì ta kí hiệu vectơ đó là \(\overrightarrow {AB}\). - Đối với vectơ \(\overrightarrow {AB}\), ta gọi:
- Đường thẳng đi qua hai điểm \(A,B\) là giá của vectơ \(\overrightarrow {AB}\).
- Độ dài đoạn thẳng \(AB\) là độ dài của vectơ \(\overrightarrow {AB}\), kí hiệu là \(\left |\overrightarrow {AB}\right|\).
- Vectơ còn được kí hiệu là \(\overrightarrow {a},\overrightarrow {b} ,...\) nếu không chỉ rõ điểm đầu điểm cuối.
Ví dụ: Cho hình vuông \(ABCD\) tâm \(O\) và có độ dài cạnh bằng \(a\). Tính độ dài các vectơ \(\overrightarrow {AC},\overrightarrow {BO}\).
Hướng dẫn giải
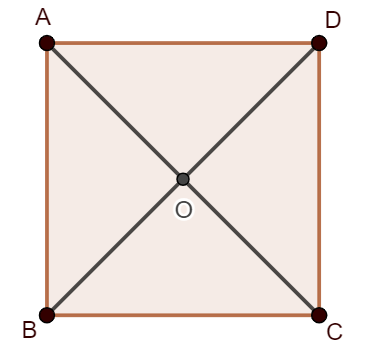
Vì cạnh của hình vuông bằng \(a\) nên độ dài đường chéo bằng \(a\sqrt2\). Do đó \(AC=BD=a\sqrt2,BO=\frac{BD}{2}=\frac{a\sqrt2}{2}\).
Vậy \(\left |\overrightarrow {AC} \right | =AC=a\sqrt2,\left |\overrightarrow {BO} \right | =BO=\frac{a\sqrt2}{2}\).
2. Phương và hướng của vectơ
- Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
- Hai vectơ cùng phương thì chúng hoặc là cùng hướng, hoặc là ngược hướng.
- Nhận xét: Ba điểm phân biệt \(A,B,C\) thẳng hàng khi và chỉ khi hai vectơ \(\overrightarrow {AB},\overrightarrow {AC}\) cùng phương.
Ví dụ: Hình vẽ bên mô tả hoạt động của ròng rọc khi dùng lực kéo một đầu. Chuyển động của các sợi dây tương ứng với các vectơ \(\overrightarrow {a},\overrightarrow {b},\overrightarrow {c}\).
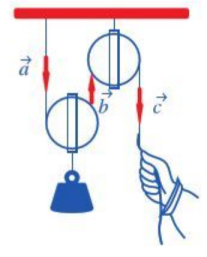
a) Hãy chỉ ra các vectơ cùng phương.
b) Hãy chỉ ra các vectơ cùng hướng, ngược hướng.
Hướng dẫn giải
a) Các vectơ \(\overrightarrow {a},\overrightarrow {b},\overrightarrow {c}\) có giá song song nên chúng cùng phương với nhau.
b) Hai vectơ \(\overrightarrow {a},\overrightarrow {c}\) là hai vectơ cùng hướng. Hai vectơ \(\overrightarrow {a},\overrightarrow {b}\)là hai vectơ ngược hướng. Hai vectơ \(\overrightarrow {b},\overrightarrow {c}\) là hai vectơ ngược hướng.
3. Hai vectơ bằng nhau, hai vectơ đối nhau
- Hai vectơ được gọi là bằng nhau nếu chúng có cùng hướng và cùng độ dài, kí hiệu \(\overrightarrow {a}=\overrightarrow {b}\).
- Hai vectơ được gọi là đối nhau nếu chúng ngược hướng và cùng độ dài, kí hiệu \(\overrightarrow {a}=-\overrightarrow {b}\). Khi đó \(\overrightarrow {b}\) được gọi là vectơ đối của \(\overrightarrow {a}\).
- Cho vectơ \(\overrightarrow {a}\) và điểm \(O\), ta luôn tìm được một điểm \(A\) duy nhất sao cho \(\overrightarrow {OA}=\overrightarrow {a}\). Khi đó độ dài của vectơ \(\overrightarrow {a}\) là độ dài đoạn \(OA\), kí hiệu \(\left | \overrightarrow a \right |\).
- Cho đoạn thẳng \(AB\), ta luôn có: \(\overrightarrow {AB} =-\overrightarrow {BA}\).
Ví dụ: Cho hình vuông \(ABCD\) có tâm \(O\). Hãy chỉ ra bốn cặp vectơ bằng nhau, bốn cặp vectơ đối nhau.
Hướng dẫn giải
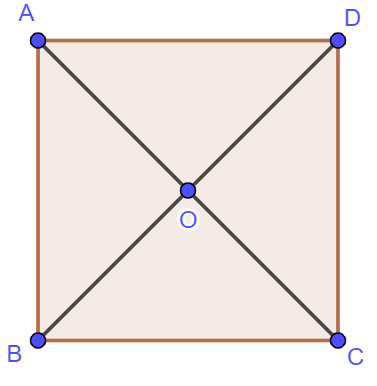
Bốn cặp vectơ bằng nhau là: \(\overrightarrow {AD}\) và \(\overrightarrow {BC}\); \(\overrightarrow {DA}\) và \(\overrightarrow {CB}\); \(\overrightarrow {AO}\) và \(\overrightarrow {OC}\); \(\overrightarrow {CO}\) và \(\overrightarrow {OA}\).
Bốn cặp vectơ đối nhau là: \(\overrightarrow {AD}\) và \(\overrightarrow {CB}\); \(\overrightarrow {DA}\) và \(\overrightarrow {BC}\); \(\overrightarrow {OA}\) và \(\overrightarrow {OC}\); \(\overrightarrow {OA}\) và \(\overrightarrow {AO}\).
4. Vectơ - không
Vectơ có điểm đầu và điểm cuối trùng nhau gọi là vectơ - không, kí hiệu \(\overrightarrow {0}\). Ta có:
- \(\left | \overrightarrow {0} \right | =0\).
- Vectơ - không luôn cùng phương, cùng hướng với mọi vectơ.
- Vectơ đối của vectơ - không là chính nó.
