Tọa độ của vectơ
Cho hệ trục 
\(Oxy\), ta có:
- Vectơ đơn vị của trục hoành là \(\overrightarrow i (1;0).\)
- Vectơ đơn vị của trục tung là \(\overrightarrow j (0;1) .\)
- Với mỗi vectơ\(\overrightarrow u\), ta luôn có: \(\overrightarrow u =x_0.\overrightarrow i+y_0.\overrightarrow j\). Trong đó \(x_0,y_0\) được gọi là hoành độ, tung độ của \(\overrightarrow u\).
- Cho hai điểm \(A\) và \(B\), khi đó \(\overrightarrow {AB}=(x_B-x_A;y_B-y_A)\).
- Hai vectơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau, tức là:
\(\overrightarrow u(x;y)=\overrightarrow v(x';y') \Leftrightarrow \left\{\begin{matrix} x=x' \\ y=y' \end{matrix}\right.\)
- Nếu điểm \(M\) có tọa độ \((x;y)\) thì vectơ \(\overrightarrow {OM}=(x;y)\)
Ví dụ 1: Trong mặt phẳng tọa độ \(Oxy\), cho \(A(1;2);B(0;1);C(-2;0)\). Tìm \(D\) sao cho tứ giác \(ABCD\) là hình bình hành.
Hướng dẫn giải
Vì tứ giác \(ABCD\) là hình bình hành nên \(\overrightarrow {AB}=\overrightarrow {DC}\).
Áp dụng công thức tính tọa độ vectơ khi biết hai điểm, ta có: \(\overrightarrow {AB}=(-1;-1)\) và \(\overrightarrow {DC}= (-2-x_D;-y_D)\).
Ta có:\(\overrightarrow {AB}=\overrightarrow {DC} \Leftrightarrow\)\(\left\{\begin{matrix} -1=-2-x_D \\ -1=-y_D \end{matrix}\right.\)\(\left\{\begin{matrix} x_D=-1 \\ y_D=1 \end{matrix}\right.\).
Vậy \(D(-1;1)\).
Ví dụ 2: Tìm tọa độ các vectơ sau:
a) \(\overrightarrow a=-3i+4j\)
b) \(\overrightarrow b=-3j\)
Hướng dẫn giải
a) Ta có: \(\overrightarrow a=-3i+4j =(-3;4)\).
b) Ta có: \(\overrightarrow b=-3j =(0;-3)\).
Ví dụ 3: Trong mặt phẳng tọa độ \(Oxy\), cho điểm \(M(1;3)\). Tìm tọa độ điểm đối xứng của \(M\) qua trục \(Ox\) và \(Oy\).
Hướng dẫn giải
Biểu diễn điểm \(M\) lên hệ trục tọa độ và lấy các điểm đối xứng của \(M\).
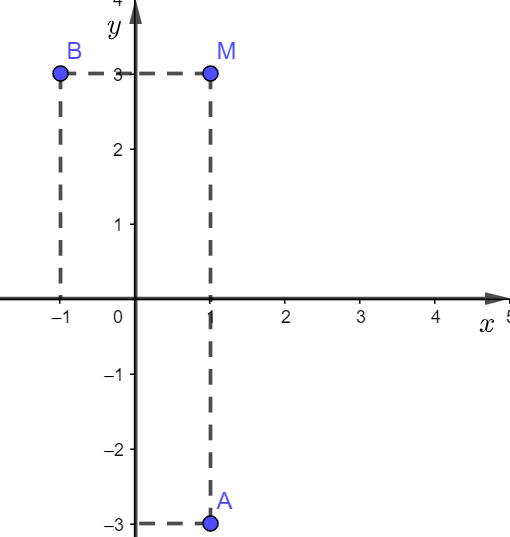
Vậy điểm đối xứng của \(M\) qua trục \(Ox\) là điểm \(A(1;-3)\).
Điểm đối xứng của \(M\) qua trục \(Oy\) là điểm \(B(-1;3)\).
