Tìm công thức hàm số bậc hai
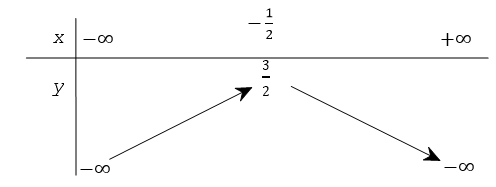
Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho ở bốn phương án A, B, C, D sau đây?
Nhận xét:
Bảng biến thiên có bề lõm hướng xuống. Loại đáp án y = 2x2 + 2x − 1 và y = 2x2 + 2x + 2.
Đỉnh của parabol có tọa độ là . Xét các đáp án, y = − 2x2 − 2x + 1 thỏa mãn.