Hãy liệt kê các phần tử của tập hợp
Cho tập hợp A = {![]() là ước chung của 36 và 120}. Hãy liệt kê các phần tử của tập hợp
là ước chung của 36 và 120}. Hãy liệt kê các phần tử của tập hợp ![]() .
.
Ta có . Do đó
.
Đề kiểm tra 15 phút Toán 10 Chương 1 Mệnh đề toán học. Tập hợp sách Cánh Diều giúp bạn học tổng hợp lại kiến thức của cả nội dung chương. Cùng nhau luyện tập nha!
Hãy liệt kê các phần tử của tập hợp
Cho tập hợp A = {![]() là ước chung của 36 và 120}. Hãy liệt kê các phần tử của tập hợp
là ước chung của 36 và 120}. Hãy liệt kê các phần tử của tập hợp ![]() .
.
Ta có . Do đó
.
Tìm số mệnh đề sai
Cho hai mệnh đề
![]() : “ Năm 2019 là năm nhuận ”;
: “ Năm 2019 là năm nhuận ”;
![]() : “ Tứ giác có 4 cạnh bằng nhau là hình vuông”;
: “ Tứ giác có 4 cạnh bằng nhau là hình vuông”;
Hãy cho biết trong các mệnh đề ![]() ,
, ![]() ,
, ![]() có bao nhiêu mệnh đề sai
có bao nhiêu mệnh đề sai
Ta có sai,
sai nên
đúng và
đúng;
Ta có đúng và
đúng nên
đúng;
Vậy trong các mệnh đề ,
,
có 0 mệnh sai.
Chọn hình vẽ thích hợp
Hình nào sau đây minh họa tập ![]() là con của tập
là con của tập![]() ?
?
Hình vẽ cần tìm là: 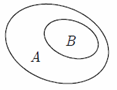
Xác định số phần tử của tập X
Cho tập hợp ![]() Tìm
Tìm ![]() .
.
Giải bất phương trình
Mà là các số tự nhiên nên chọn đáp án
.
Phủ định mệnh đề đã cho
Cho mệnh đề: “![]() ”. Mệnh đề phủ định của mệnh đề trên là
”. Mệnh đề phủ định của mệnh đề trên là
Mệnh đề phủ định của mệnh đề đã cho là “”
Hai tập hợp bằng nhau
Trong các tập hợp sau đây, tập hợp nào bằng tập hợp ![]() :
:
Ta có:
Tập hợp là tập hợp
.
Vậy tập hợp
Tìm mệnh đề
Trong số các câu sau, câu nào là mệnh đề?
Các câu trong đáp án “Thời tiết hôm nay thật đẹp!”, “Các bạn có làm được bài kiểm tra này không” và “Chúc các bạn đạt điểm như mong đợi!” đều là các câu cảm thán hoặc câu hỏi nên ta loại, chỉ có đáp án “Số chia hết cho
” là câu khẳng định.
Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp là?
Lớp ![]() có
có ![]() học sinh giỏi Toán,
học sinh giỏi Toán, ![]() học sinh giỏi Lý,
học sinh giỏi Lý, ![]() học sinh giỏi Hóa,
học sinh giỏi Hóa, ![]() học sinh giỏi cả Toán và Lý,
học sinh giỏi cả Toán và Lý, ![]() học sinh giỏi cả Toán và Hóa,
học sinh giỏi cả Toán và Hóa, ![]() học sinh giỏi cả Lý và Hóa,
học sinh giỏi cả Lý và Hóa, ![]() học sinh giỏi cả
học sinh giỏi cả ![]() môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp
môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp ![]() là:
là:
Ta dùng biểu đồ Ven để giải

Nhìn vào biểu đồ, số học sinh giỏi ít nhất trong
môn là:
Phủ định mệnh đề
Cho ![]() là số tự nhiên. Phủ định của mệnh đề “
là số tự nhiên. Phủ định của mệnh đề “![]() chẵn,
chẵn, ![]() là số chẵn” là mệnh đề:
là số chẵn” là mệnh đề:
Mệnh đề phủ định là “ lẻ,
lẻ”.
Xác định câu là mệnh đề
Trong các câu sau, câu nào là mệnh đề?
Đáp án cần tìm là: “Nha Trang là một thành phố ven biển ở Việt Nam”.
Chọn đáp án chính xác
Viết mệnh đề sau bằng cách sử dụng kí hiệu ![]() hoặc
hoặc ![]() : “Có một số nguyên bằng bình phương của chính nó”.
: “Có một số nguyên bằng bình phương của chính nó”.
Đáp án cần tìm là: .
Tìm câu là mệnh đề
Trong các câu sau, có bao nhiêu câu là mệnh đề ?
a) Mấy giờ rồi?
b) Buôn Mê Thuột là thành phố của Đắk Lắk.
c) ![]() là số nguyên tố.
là số nguyên tố.
d) Làm việc đi !
“Mấy giờ rồi ?” đây là câu hỏi nên không phải câu mệnh đề.
“Buôn Mê Thuột là thành phố của Đắk Lắk” đây là câu khẳng định đúng nên là một mệnh đề.
“ là số nguyên tố ” đây là câu khẳng định sai nên là một mệnh đề.
“Làm việc đi !” đây là câu cảm thán nên không phải là mệnh đề.
Tìm tham số m thỏa mãn điều kiện
Cho hai tập hợp ![]() ,
, ![]() . Tìm m để
. Tìm m để ![]() .
.
Biểu diễn tập hợp trên trục số
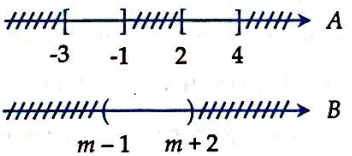
Ta đi tìm m để
hay
Xác định tập hợp A hợp B
Cho hai tập hợp ![]() . Xác định tập hợp
. Xác định tập hợp ![]()
Ta có:
Chọn đáp án đúng
Kết quả của phép toán ![]() là
là
Ta có .
Tìm câu sai
Trong các mệnh đề sau, mệnh đề nào sai?
+ Xét đáp án “,
![]() chia hết cho
chia hết cho .”.
Khi thì giá trị của
bằng
nên đáp án đúng
+ Xét đáp án “,
![]() chia hết cho
chia hết cho ”.
Khi không chia hết cho
,
.
Khi không chia hết cho
,
.
+ Xét đáp án Tồn tại số nguyên tố chia hết cho .. Tồn tại số nguyên tố
chia hết cho
nên đáp án đúng
+ Xét đáp án “,
”. Phương trình
nên đáp án đúng.
Chọn phương án thích hợp
Tập hợp nào sau đây chỉ gồm các số vô tỷ?
Tập hợp chỉ gồm các số vô tỷ là .
Chọn đáp án đúng
Cho tập hợp ![]() và
và ![]() . Có bao nhiêu tập
. Có bao nhiêu tập ![]() thỏa mãn
thỏa mãn ![]() ?
?
Có 4 tập hợp thỏa mãn
là:
;
;
và
.
Xác định giao của hai tập hợp
Cho hai tập hợp ![]() khi đó tập
khi đó tập ![]() là
là
Ta tìm phần chung của cả hai tập hợp. Khi đó đáp án là:
Mệnh đề nào sau đây đúng?
Cho ![]() là số tự nhiên, mệnh đề nào sau đây đúng?
là số tự nhiên, mệnh đề nào sau đây đúng?
Với thì
là hai số tự nhiên liên tiếp
là số chẵn
Với thì
là ba số tự nhiên liên tiếp
trong 3 số
có 1 số chia hết cho
Chọn đáp án là số chia hết cho
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
