Giải tam giác
Cho tam giác 
\(ABC\), ta kí hiệu:
- \(AB=c,BC=a,CA=b\);
- \(h_a,h_b,h_c\) lần lượt là độ dài các đường cao kẻ từ \(A,B,C\);
- \(R\) là bán kính đường tròn ngoại tiếp;
- \(r\) là bán kính đường tròn nội tiếp;
- \(p= \frac{a+b+c}2\) là nửa chu vi;
- \(S\) là diện tích tam giác \(ABC\).
Ta có các công thức tính diện tích tam giác sau:
- \(S_{ABC}=\frac12 a.h_a=\frac12 b.h_b =\frac12 c.h_c\);
- \(S_{ABC}=\frac12bc\sin A=\frac12ac\sin B=\frac12ab\sin C\);
- \(S_{ABC}=\frac {abc}{4R}\);
- \(S_{ABC}=p.r\);
- \(S_{ABC}=\sqrt{p(p-a)(p-b))p-c)}\) (Công thức Heron).
Ví dụ 1: Cho tam giác \(ABC\) có \(a=5,b=6,c=7\). Tính diện tích tam giác \(ABC\).
Hướng dẫn giải
(Khi biết 3 cạnh của tam giác, ta sử dụng công thức Heron)
Ta có: \(p=\frac{a+b+c}2=\frac{5+6+7}2=9\).
Áp dụng công thức Heron:
\(S_{ABC}=\sqrt{p(p-a)(p-b))p-c)}\)\(=\sqrt{9(9-5)(9-6)(9-7)} = 6\sqrt6\).
Ví dụ 2: Cho tam giác \(ABC\) có \(c=3,b=4,\hat A=120^{\circ}\). Tính diện tích tam giác này.
Hướng dẫn giải
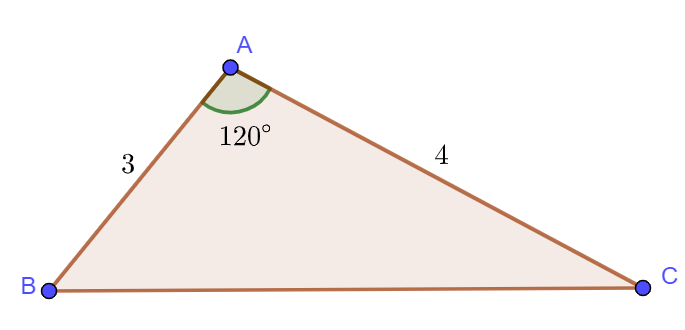
(Khi biết 2 cạnh và 1 góc xen giữa, ta sử dụng công thức số 2)
Ta có: \(S_{ABC}=\frac12bc\sin A=\frac12.3.4\sin 120^{\circ} =3\sqrt3\).
2. Giải tam giác
Giải tam giác là đi tìm số đo tất cả các cạnh và tất cả các góc của tam giác.
Ví dụ: Giải tam giác \(ABC\) biết \(a=4,\hat B=60^{\circ} ,\hat C=45^{\circ}\).
Hướng dẫn giải
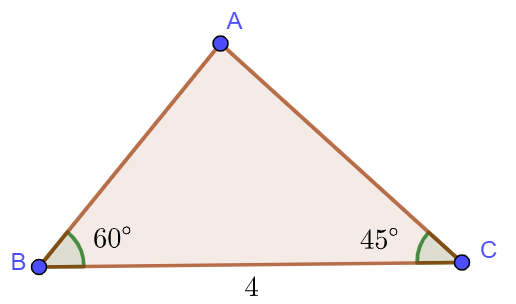
Ta có: \(\hat A=180^{\circ} -(\hat B+\hat C)\)\(=180^{\circ} -(60^{\circ} +45^{\circ} )=75^{\circ}\).
Áp dụng định lý sin, ta có: \(\frac{4}{\sin 75^{\circ} }=\frac b{\sin 60^{\circ}}=\frac c{\sin45^{\circ}}=2R\).
Suy ra: \(b=\sin 60^{\circ} .\frac 4{\sin 75^{\circ} } \approx 3,59\), \(x=\sin 45^{\circ} .\frac 4{\sin 75^{\circ} } \approx =2,93\), \(R=\frac 4{2\sin 75^{\circ} } \approx 2,07\).
