Giá trị lượng giác của một góc từ 0 đến 180 độ. Định lí côsin và định lí sin trong tam giác
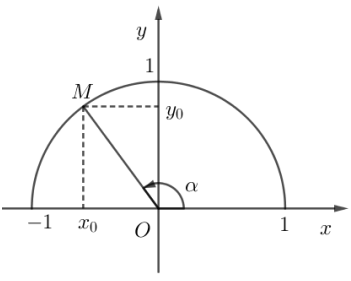
Trong mặt phẳng tọa độ 
\(Oxy\), nửa đường tròn tâm \(O\) nằm phía trên trục hoành có bán kính \(R=1\) được gọi là nửa đường tròn đơn vị.
Với mỗi góc \(\alpha\) (\(0^{\circ} \le \alpha \le 180^{\circ}\)) ta xác định một điểm \(M\) trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha\) và điểm \(M\) có tọa độ \(M(x_0;y_0)\). Khi đó:
- \(\sin\) của góc \(\alpha\) là \(y_0\), kí hiệu \(\sin \alpha = {y_0}\).
- côsin của góc \(\alpha\) là \(x_0\), kí hiệu \(\cos \alpha =x_0\).
- tang của góc \(\alpha\) là \(\frac{y_0}{x_0}\) (\(x_0 \neq 0\)), kí hiệu \(\tan \alpha = \frac{y_0}{x_0}\).
- côtang của góc \(\alpha\) là \(\frac {x_0}{y_0}\) (\(y_0 \neq 0\)), kí hiệu \(\cot \alpha = \frac {x_0}{y_0}\).
Các số \(\sin \alpha ; \cos \alpha; \tan \alpha ; \cot \alpha\) là các giá trị lượng giác của góc \(\alpha\).
2. Quan hệ giữa các giá trị lượng giác bù nhau
- \(\sin \alpha = \sin (180^{\circ} -\alpha)\)
- \(\cos \alpha = -\cos (180^{\circ} -\alpha)\)
- \(\tan \alpha = -\tan (180^{\circ} -\alpha)\)
- \(\cot \alpha = -\cot (180^{\circ} -\alpha)\)
Ví dụ: Đơn giản hóa các biểu thức sau:
a) \(\sin 110^{\circ} +\cos 50^{\circ} -\sin70^{\circ} +\cos130^{\circ}\);
b) \(-2\sin (180^{\circ} -\beta).\cot \beta + 3\cos \beta +\cos(180^{\circ} -\beta)\).
Hướng dẫn giải
a) \(\sin 110^{\circ} +\cos 50^{\circ} -\sin70^{\circ} +\cos130^{\circ}\)\(= (\sin 110^{\circ} -\sin70^{\circ}) +(\cos130^{\circ}+\cos 50^{\circ})\)\(= (\sin (180^\circ - 110^{\circ}) -\sin70^{\circ})\)\(+(\cos130^{\circ}-\cos (180^{\circ} -50^{\circ}))\)\(=(\sin 70^{\circ} -\sin 70^{\circ} )+(\cos 130^{\circ} -\cos 130^{\circ} )=0\).
b) \(-2\sin (180^{\circ} -\beta).\cot \beta + 3\cos \beta +\cos(180^{\circ} -\beta)\)=\(-2\sin \beta.\cot \beta + 3\cos \beta -\cos\beta\)\(-2\sin \beta. \frac {\cos\beta} {\sin \beta} + 3\cos \beta -\cos\beta =\)\(-2\cos\beta + 3\cos \beta -\cos\beta=0\).
3. Giá trị lượng giác của các góc đặc biệt
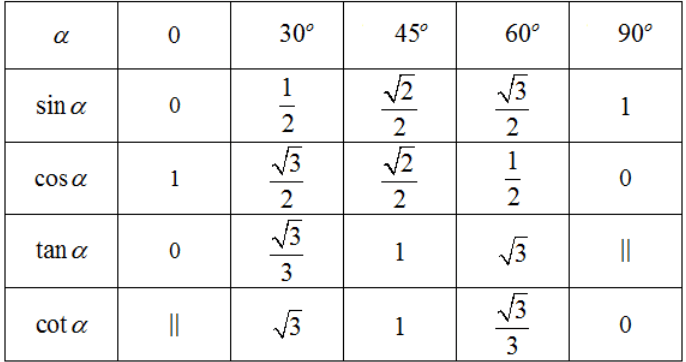
Chú ý: Trong bảng trên, kí hiệu || để chỉ các giá trị lượng giác không xác định.
Ví dụ: Cho góc \(\alpha\) (\(0^{\circ} < \alpha <180^{\circ}\)) thỏa mãn \(\tan \alpha =2\). Hãy tính giá trị biểu thức \(S= \frac {3\sin\alpha +2\cos\alpha}{2\sin\alpha -3\cos\alpha}\).
Hướng dẫn giải
Vì \(\tan \alpha =\frac {\sin\alpha}{\cos\alpha}\) nên:
Chia cả tử cả mẫu cho \(\cos\alpha\), ta được: \(S= \frac {3\tan\alpha +2}{2\tan\alpha -3}\)\(= \frac {3.2+2}{2.2 -3}=8\).
4. Định lý côsin trong tam giác
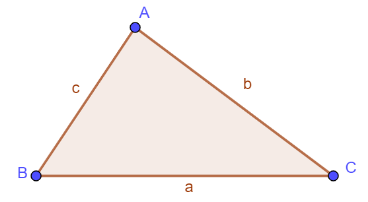
Cho tam giác \(ABC\) có \(AB=a,BC=c,AC=b\), ta có:
- \(a^2=b^2+c^2-2bc\cos A\)
- \(b^2=a^2+c^2-2ac\cos B\)
- \(c^2=a^2+b^2-2ab\cos C\)
Hệ quả
- \(\cos A=\frac{b^2+c^2-a^2}{2bc}\)
- \(\cos B=\frac{a^2+c^2-b^2}{2ac}\)
- \(\cos C=\frac{a^2+b^2-c^2}{2ab}\)
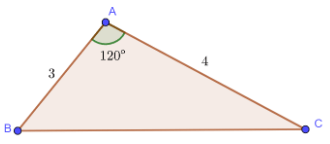
Ví dụ 1: Cho tam giác \(ABC\) có \(\hat{A} =120^{\circ}\) và \(AB=3,AC=4\). Tính độ dài cạnh \(BC\).
Hướng dẫn giải
Áp dụng định lí côsin trong tam giác \(ABC\), ta có:
\(BC^2=AB^2+AC^2-2AB.AC.\cos A\)\(=3^2+4^2-2.3.4.\cos 60^{\circ} =13\)
Suy ra \(BC=\sqrt{13}\).
Ví dụ 2: Cho tam giác \(ABC\) có \(a=19,b=6,c=15\). Tính giá trị góc \(\hat A\). (kết quả làm tròn đến hàng phần trăm)
Hướng dẫn giải
Áp dụng hệ quả của định lý côsin cho tam giác \(ABC\):
\(\cos A= \frac{b^2+c^2-a^2}{2bc}\)\(=\frac{6^2+15^2-19^2}{2.6.15}=-\frac59\)
Suy ra \(\hat A\approx 123,75^{\circ}\).
2. Định lý sin trong tam giác
Cho tam giác \(ABC\) có \(AB=c,BC=a,CA=b\) và \(R\) là bán kính đường tròn ngoại tiếp tam giác \(ABC\), ta có:
\(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\)
Ví dụ: Cho tam giác \(ABC\) có \(\hat A=120^{\circ} ,\hat C=45^{\circ} ,b=6\). Tính số đo góc \(\hat B\), độ dài \(a,c,R\). (kết quả làm tròn đến hàng phần trăm)
Hướng dẫn giải
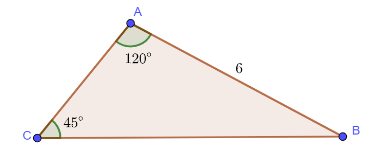
Ta có: \(\hat B=180^{\circ} -(\hat A+\hat C)\)\(=180^{\circ}-(120^{\circ} +45^{\circ} )=15^{\circ}\)
Áp dụng định lý sin trong tam giác \(ABC\):
\(\frac{a}{\sin 120^{\circ} }=\frac 6{\sin 15^{\circ}}=\frac c{\sin45^{\circ}}=2R\)
Suy ra: \(a=\sin 120^{\circ} .\frac 6{\sin 15^{\circ} } \approx 20,08\)\(c=\sin 45^{\circ} .\frac 6{\sin 15^{\circ} } \approx 16,39\)
\(R=\frac 6{2\sin 15^{\circ} }\approx 11,59\).
