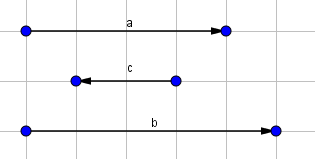
Khẳng định nào sau đây đúng?
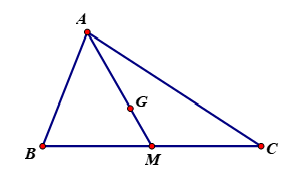
Cho tam giác ![]() và điểm
và điểm ![]() thỏa mãn
thỏa mãn ![]() Khẳng định nào sau đây đúng?
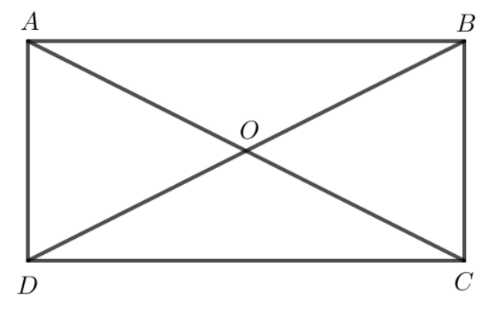
Khẳng định nào sau đây đúng?
Gọi lần lượt là trung điểm
và trọng tâm tam giác
Vì
là trung điểm
nên
Theo bài ra, ta có suy ra
thẳng hàng
Mặt khác là trọng tâm của tam giác
Do đó, ba điểm
thẳng hàng.