20 đề ôn tập học kì 1 lớp 12 môn Toán có đáp án
Đề ôn thi học kì 1 Toán 12
Lớp:
Lớp 12
Môn:
Toán
Loại File:
PDF
Phân loại:
Tài liệu Tính phí

20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12
NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 1
ĐỀ ÔN TẬP SỐ 01
Câu 1. [2D1-1.2-1] Hỏi hàm số
4
2 1
y x
đồng biến trên khoảng nào?
A.
0;
. B.
1
;
2
. C.
;0
. D.
1
;
2
.
Lời giải
Chọn A
Ta có
3
' 8 , ' 0 0
y x y x
. Nên hàm số đã cho đồng biến trên
0;
Câu 2. [2D1-2.5-1] Số điểm cực trị của hàm số
3 2
3 1y x x x
là
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Chọn A
Hàm số bậc ba đã cho có
2
' 3 6 1y x x
là tam thức bậc 2 có 2 nghiệm phân biệt nên hàm số
đã cho có 2 cực trị.
Câu 3. [2D1-3.3-1] Tìm giá trị lớn nhất của hàm số
3 2
3y x x
trên đoạn
2;1
A.
2;1
max 2
y
. B.
2;1
max 0
y
. C.
2;1
max 20
y
. D.
2;1
max 54
y
.
Lời giải
Chọn C
2
' 3 6 0 0
y x x x
(thỏa mãn) hoặc
2
x
(loại)
2 20; 0 0; 1 2
y y y
Vậy:
2;1
max 20
y
Câu 4. [2D1-4.3-1] Đồ thị hàm số
2 1
2
x
y
x
có các đường tiệm cận là:
A.
2
y
và
2
x
. B.
2
y
và
2
x
. C.
2
y
và
2
x
. D.
2
y
và
2
x
.
Lời giải
Chọn B
Nhắc lại đồ thị hàm số
ax b
y
cx d
có đường tiệm cận ngang là
a
y
c
và đường tiệm cận đứng
là
d
x
c
.
Câu 5. [2D1-5.2-1] Cho đồ thị như hình vẽ bên. Đây là đồ thị của hàm số nào?
VnDoc.com
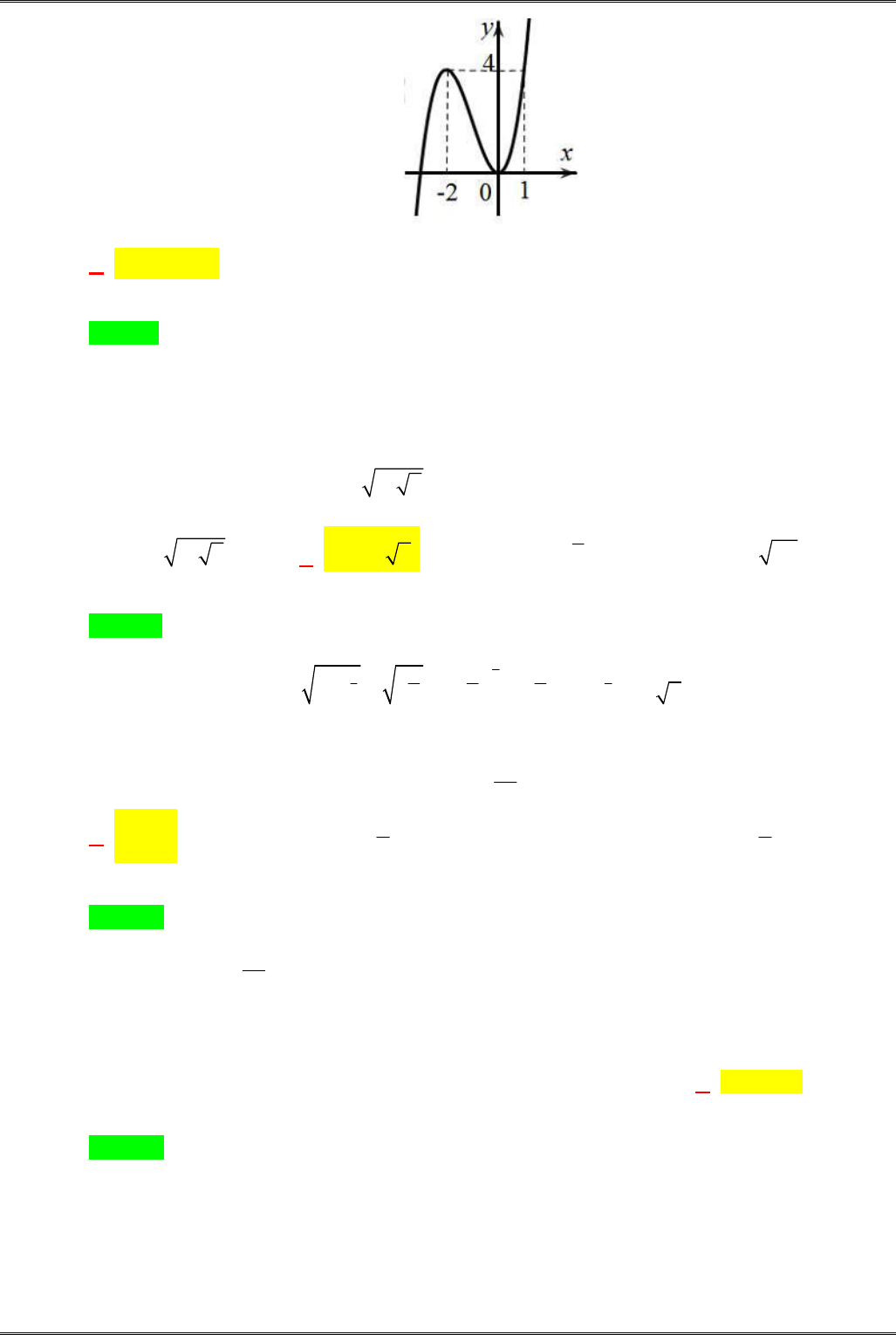
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12
NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 2
A.
3 2
3y x x
. B.
3 2
3y x x
. C.
3 2
3y x x
. D.
3 2
3 1
y x x
Lời giải
Chọn A
Khi
x
tiến tới
thì
y
tiến tới
, do đó hệ số của
3
x
phải dương
Loại B, C
Hàm số đi qua điểm
0;0
nên hàm số ở ý D không thỏa mãn
Câu 6. [2D2-1.2-1] Cho biểu thức
4
3
P x x
với
x
là số dương khác
1
. Khẳng định nào sau đây
sai?
A.
2
3
P x x x
.
B.
2
3
.P x x
. C.
13
6
P x
. D.
6
13
P x
.
Lời giải
Chọn B.
Với
0,
x
1x
thì
1
1 13 13 13 1
2
4 2 2
6
3 3 3 6 6
. .
P x x x x x x x x x
.
Câu 7. [2D2-2.1-1] Tính giá trị của biểu thức
2
1
log
a
A
a
, với
0
a
và
1
a
A.
2A
. B.
1
2
A
. C.
2A
. D.
1
2
A
.
Lời giải
Chọn A.
Ta có:
2
2
1
log log 2.log 2
a a a
A a a
a
.
Câu 8. [2H1-2.1-1] Khi tăng độ dài tất cả các cạnh của một khối hộp chữ nhật lên gấp đôi thì thể tích
khối hộp tương ứng sẽ:
A. tăng 2 lần. B. tăng 4 lần. C. tăng 6 lần. D. tăng 8 lần.
Lời giải
Chọn D.
Giả sử chiều dài, chiều rộng, chiều cao của khối hộp chữ nhật là
, , a b c
.
Thể tích của khối hộp là
V abc
.
Khi tăng tất cả các cạnh của khối hộp lên gấp đôi thì thể tích khối hộp thu được là
’ 2 .2 .2 8 8V a b c abc V
VnDoc.com
20 ĐỀ ÔN THI HỌC KÌ 1 TOÁN 12
NHÓM SOẠN ĐỀ ÔN THI HK1 – TOÁN 12 Trang 3
Câu 9. [2H1-2.2-1] Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
A
,
3 , 4AB a AC a
,
SB
vuông góc
ABC
,
5 2SC a
. Tính thể tích khối chóp
.
S ABC
theo
a
.
A.
3
10a
. B.
3
30a
. C.
3
10 2
a
. D.
3
5a
.
Lời giải
Chọn A.
Bước 1: Diện tích tam giác vuông tại
A
:
1
. .
2
ABC
S AB AC
.
Bước 2: Tính độ dài đường cao
2 2
SB SC BC
.
Bước 3: Thể tích khối chóp
3
.
1
. . 10
2
S ABC ABC
V S SB a
(đvtt).
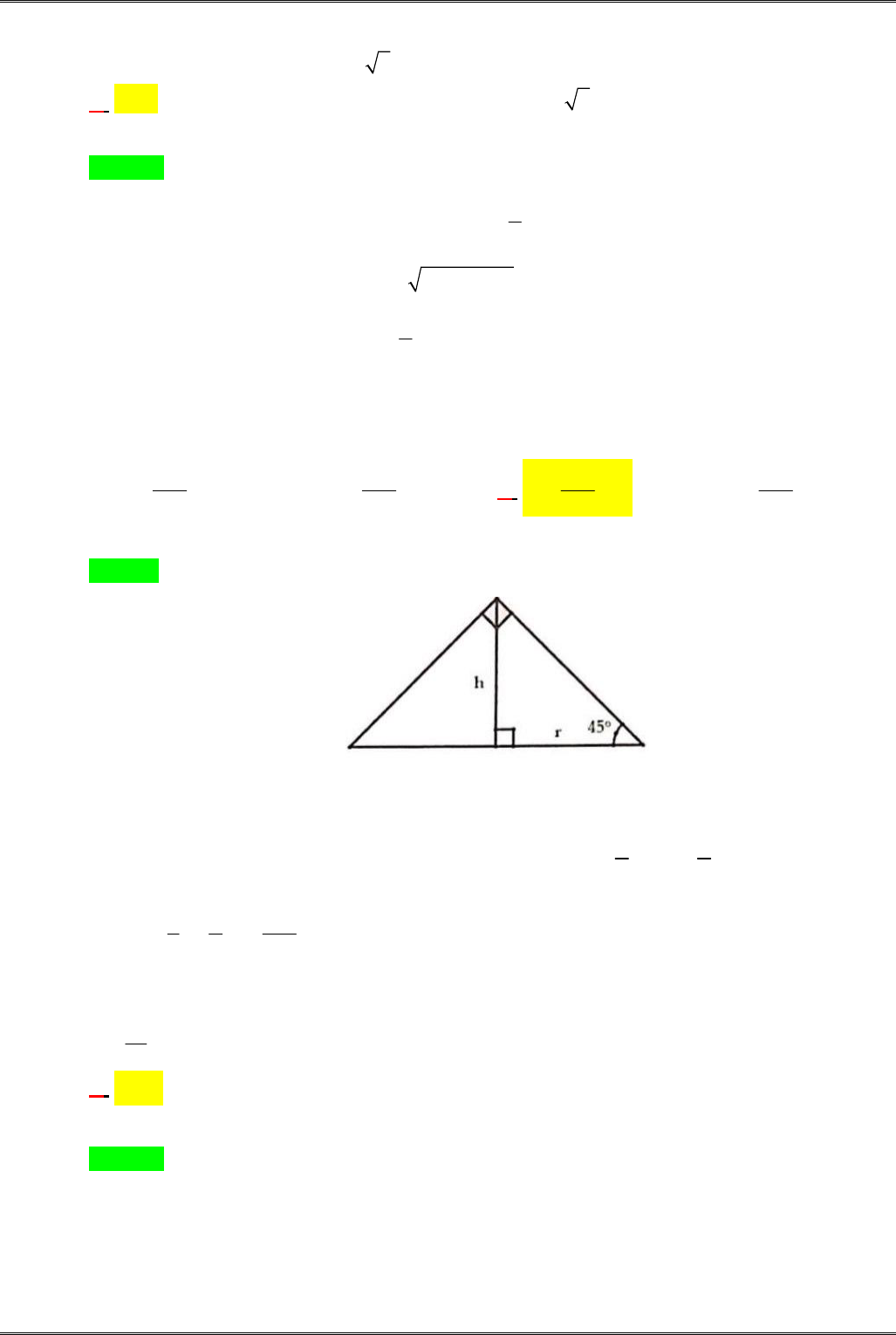
Câu 10. [2H2-1.4-1] Cho hình nón
N
có thiết diện qua trục là một tam giác vuông có cạnh huyền
bằng
a cm
. Tính thể tích
V
của khối nón đó.
A.
3
3
8
a
V cm
. B.
3
3
6
a
V cm
. C.
3
3
24
a
V cm
. D.
3
3
3
a
V cm
.
Lời giải
Chọn C
Thiết diện qua trục của hình nón sẽ là một tam giác cân, từ giả thiết suy ra tam giác vuông cân.
Đường cao từ đỉnh có góc vuông của thiết diện chính là đường cao của hình nón và độ dài cạnh
huyền chính là đường kính đáy của hình nón. Do đó ta có:
2
a
r
và
2
a
h
.
Vậy
3
3
3
1
3 2 24
a a
V cm
.
Câu 11. [2D1-2.7-2] Tìm tất cả các giá trị của tham số thực
m
sao cho hàm số
3
2 2
2 1
3
x
y x m m x
có 2 điểm cực trị.
A.
1
m
. B.
m
. C.
1
m
. D.
;1
m
.
Lời giải
Chọn A.
TXĐ:
D
. Ta có:
2 2
' 2 2 2 ; ' 0
2
x m
y x x m m x m x m y
x m
.
Hàm số có 2 điểm cực trị
' 0
y
có 2 nghiệm phân biệt
2 1
m m m
.
VnDoc.com
Đề ôn tập học kì 1 môn Toán lớp 12
VnDoc xin giới thiệu tới bạn đọc 20 đề ôn tập học kì 1 lớp 12 môn Toán có đáp án. Chắc chắn tài liệu sẽ giúp các bạn giải Toán 12 nhanh và chính xác hơn. Mời các bạn học sinh tham khảo.



