36 Bài toán thực tế về phương trình bất phương trình mũ và lôgarit
Toán lớp 11
Lớp:
Lớp 11
Môn:
Toán
Dạng tài liệu:
Chuyên đề
Loại File:
Word + PDF
Phân loại:
Tài liệu Tính phí
CÁC DẠNG TOÁN THỰC LŨY THỪA-LOGARIT. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. Phép tính luỹ thừa với số mũ nguyên
Cho số thực
a
khác 0 và số nguyên dương
n
. Ta đặt
1
n
n
a
a
.
Chú ý
0
0
và
0
n
(
n
nguyên dương) không có nghĩa.
Luỹ thừa với số mũ nguyên có các tính chất tương tự của luỹ thừa với số mũ nguyên dương.
2. Căn bậc
n
a) Định nghĩa
Cho số thực
a
và số nguyên dương
2nn
. Số
b
được gọi là căn bậc
n
của số
a
nếu
n
ba
.
Nhận xét
Với
n
lẻ và
aR
: Có duy nhất một căn bậc
n
của
a
, kí hiệu là
n
a
.
Với
n
chẵn, ta xét ba trường hợp sau:
+)
0a
: Không tồn tại căn bậc
n
của
a
;
+)
0a
: Có một căn bậc
n
của
a
là số 0 ;
+)
0a
: Có hai căn bậc
n
của
a
là hai số đối nhau, giá trị dương kí hiệu là
n
a
, còn giá trị âm kí hiệu là
n
a
.
b) Tính chất
nêu le
nêu chan;
nn
an
a
an
n n n
a b ab
;
n
n
n
aa
b
b
()
m n m
n
aa
n
k nk
aa
.
(Ở mỗi công thức trên, ta giả sử các biểu thức xuất hiện trong đó là có nghĩa).
3. Phép tính luỹ thừa với số mũ hữu tỉ
Cho số thực
a
dương và số hữu tỉ
m
r
n
, trong đó
, , 2m n n ZN
. Luỹ thừa của
a
với số mũ
r
xác định
bởi:
m
r n m
n
a a a
.
Nhận xét
1
( 0, , 2)
n
n
a a a n n N
.
Luỹ thừa với số mũ hữu tỉ của số thực dương có đầy đủ các tính chất của luỹ thừa với số mũ nguyên.
4. Phép tính luỹ thừa vói số mũ thực
a) Định nghĩa
Cho
a
là số thực dương,
là số vô tỉ,
n
r
là dãy số hữu tỉ và
lim
n
r
. Giới hạn của dãy số
n
r
a
gọi là luỹ
thừa của
a
với số mũ
, kí hiệu
, lim
n
r
a a a
.
b) Tính chất

Cho
,ab
là những số thực dương;
,
là những số thực tuỳ ý. Khi đó, ta có:
;a a a
( ) ;ab a b
;
aa
bb
;
a
a
a
;aa
Nếu
1a
thì
aa
.
Nếu
01a
thì
aa
.
Cho
0,ab
là một số thực. Ta có:
0; 0.a b a b
5. Khái niệm lôgarit
a) Định nghĩa
Với
0, 1aa
và
0b
, ta có:
log
c
a
c b a b
. Ngoài ra:
Lôgarit thập phân của
b
là lôgarit cơ số 10 của số thực dương
b
:
log 10 ;
c
c b b
Lôgarit tự nhiên của
b
là lôgarit cơ số
e
của số thực dương
b
:
ln .
c
c b e b
b) Tính chất
Với
0, 1aa
và
0b
, ta có:
log 1 0
a
log 1
a
a
log
c
a
ac
log b
ab
‡
.
6. Một số tính chất của phép tính lôgarit
Trong mục này, ta xét
0, 1aa
và
0b
.
a) Lôgarit của một tích, một thương
Với
0, 0mn
, ta có:
log log log
a a a
mn m n
;
log log log
a a a
m
mn
n
Nhận xét:
1
log log
aa
b
b
.
b) Lôgarit của một luỹ thừa
Với mọi số thực
, ta có:
log log
aa
bb
.
Nhận xét: Với mọi số nguyên dương
2n
, ta có:
1
log log
n
aa
bb
n
.
c) Đổi cơ số của lôgarit
Với
,ab
là hai số thực dương khác 1 và
c
là số thực dương, ta có:
log
log
log
a
b
a
c
c
b
.
Nhận xét: Với
,ab
là hai số thực dương khác
1, 0c
và
0
, ta có những công thức sau:
11
log .log log ; log ; log log
log
a
a b a a a
a
b
b c c b b b
a
.
7. Hàm số mũ
Cho số thực
( 0, 1)a a a
. Hàm số
x
ya
được gọi là hàm số mũ cơ số
a
.
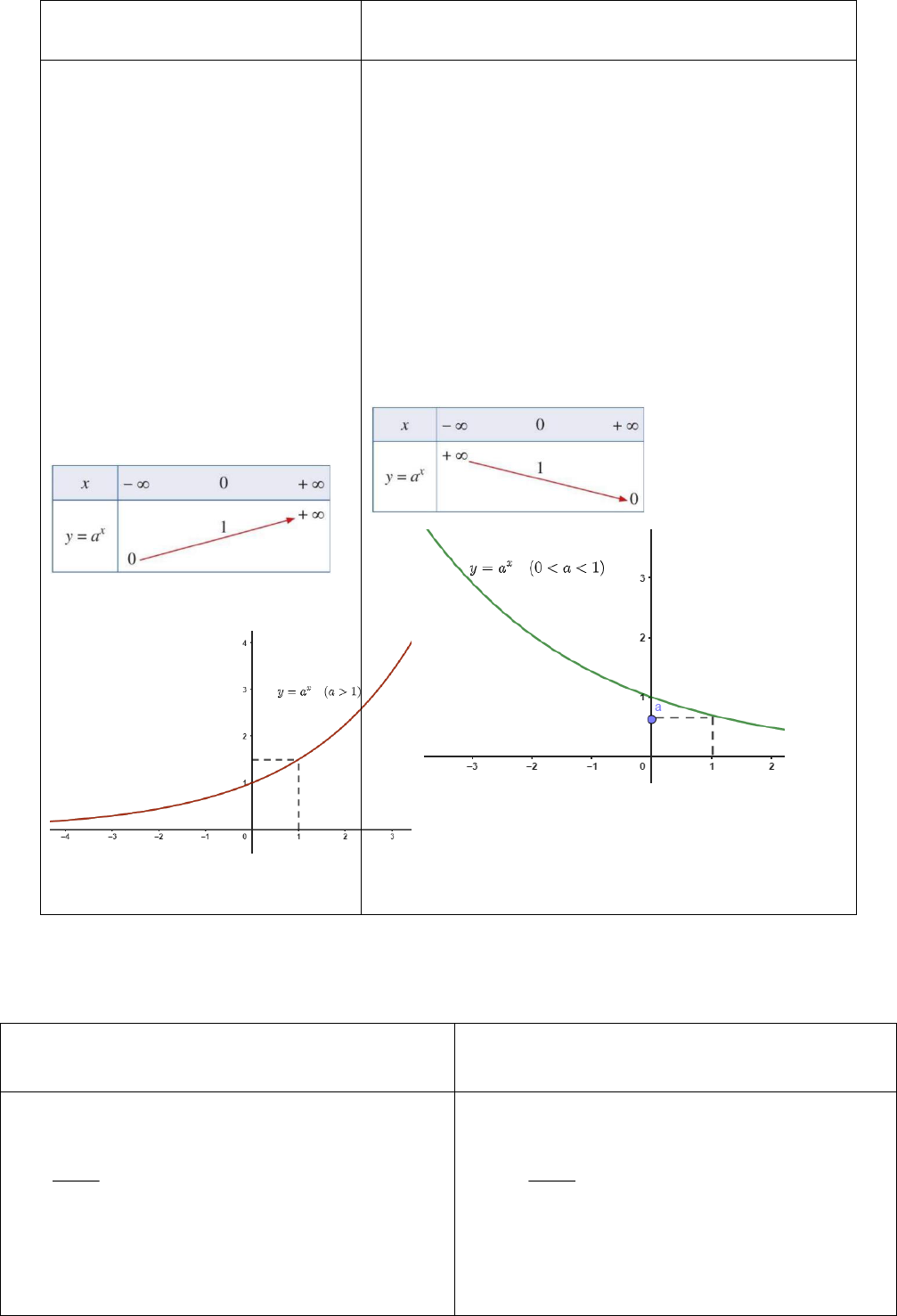
Xét hai trường hợp:
( 1)
x
y a a
(0 1)
x
y a a
Tập xác định:
R
; tập giá trị:
0;
.
Tính liên tục
Hàm số
( 1)
x
y a a
là hàm số liên tục
trên
R
.
Giới hạn đặc biệt
lim 0, lim .
xx
xx
aa
Sự biến thiên
Hàm số đồng biến trên
R
.
Bảng biến thiên
Đồ thị
Tập xác định:
R
; tập giá trị:
0;
.
Tính liên tục
Hàm số
(0 1)
x
y a a
là hàm số liên tục trên
R
.
Giới hạn đặc biệt
lim , lim 0.
xx
xx
aa
Sự biến thiên
Hàm số nghịch biến trên
R
.
Bảng biến thiên
Đồ thị
8. Hàm số lôgarit
Cho số thực
( 0, 1)a a a
. Hàm số
log
a
yx
được gọi là hàm số lôgarit cơ số
a
. Xét hai trường hợp:
log , 1
a
y x a
log , 0 1
a
y x a
1. Tập xác định:
(0; )
2. Sự biến thiên.
1
' 0, 0
ln
yx
xa
hàm số luôn đồng biến trên
(0; )
Giới hạn đặc biệt:
0
lim log , lim log .
aa
x
x
xx
1. Tập xác định:
(0; )
2. Sự biến thiên.
1
' 0, 0
ln
yx
xa
hàm số luôn nghịch biến
(0; )
Giới hạn đặc biệt:
0
lim log , lim log .
aa
x
x
xx
Bài toán thực tế về phương trình bất phương trình mũ và lôgarit lớp 11
Bài toán thực tế về phương trình bất phương trình mũ và lôgarit là tài liệu hữu ích giúp bạn đọc có thể trau dồi, luyện tập nội dung kiến thức về phần phương trình bất phương trình mũ và lôgarit lớp 11. Bài viết gồm có 2 phần: Kiến thức cơ bản cần nhớ và 36 bài tập vận dụng. Bài viết có đáp án và lời giải chi tiết kèm theo. Mời các bạn cùng theo dõi chi tiết bài viết dưới đây để có thêm tài liệu học môn Toán lớp 11 nhé.


