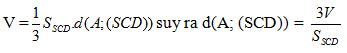Đề thi giáo viên giỏi môn Toán cấp THPT trường THPT Tân Châu, An Giang năm học 2014 - 2015

Đề thi giáo viên giỏi môn Toán cấp THPT

Đề thi giáo viên giỏi môn Toán cấp THPT trường THPT Tân Châu, An Giang năm học 2014 - 2015 có đáp án đi kèm, được VnDoc.com sưu tầm và đăng tải nhằm giúp thầy cô dễ dàng ôn tập, không mất nhiều thời gian trong việc tìm kiếm tư liệu tham khảo.

Đề thi Giáo viên dạy giỏi cấp THPT Thuận Thành số 1 tỉnh Bắc Ninh năm 2013

Đề thi giáo viên dạy giỏi tỉnh Hòa Bình năm 2013 môn Toán

Bài 1: (2 điểm)

Thầy (cô) hãy nêu quy trình trên lớp của phương pháp dạy học hợp tác theo nhóm nhỏ.

Bài 2: (2 điểm)

Thầy (cô) hãy nêu các hoạt động dạy khái niệm mới: "Lôgarit"

(Trang 82 sách giáo khoa giải tích lớp 12 nâng cao nhà xuất bản GD)

Bài 3: (2 điểm)

Thầy (cô) hãy nêu các bước hướng dẫn học sinh giải bài toán:

"Tìm m để phương trình có nghiệm thực"

Bài 4: (3 điểm)

Thầy (cô) hãy nêu 3 cách giải bài toán sau:

"Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA ⊥ (ABCD). Biết SA = a√2. Tìm khoảng cách từ điểm A đến mp(SCD)?"

Đáp án đề thi giáo viên giỏi môn Toán cấp THPT

Bài 1: Quy trình trên lớp của dạy học hợp tác theo nhóm nhỏ:

a. Làm việc chung cả lớp:

• Nêu vấn đề, xác định nhiệm vụ nhận thức.
• Tổ chức các nhóm, giao nhiệm vụ cho các nhóm.
• Hướng dẫn cách làm việc theo nhóm

b. Làm việc theo nhóm:

• Phân công trong nhóm từng cá nhân làm việc độc lập.
• Trao đổi ý kiến, thảo luận trong nhóm.
• Cử đại diện (hoặc phân công trước) chịu trách nhiệm trình bày kết quả làm việc của nhóm

c. Thảo luận, tổng kết trước toàn lớp:

• Các nhóm lần lượt báo cáo kết quả.
• Thảo luận chung.
• Giáo viên tổng kết, đặt vấn đề tiếp theo

Bài 2:

Việc dạy khái niệm mới có thể tiến hành bởi các HĐ sau:

HĐ1: Là HĐ tạo động cơ học khái niệm mới (xuất phát từ chướng ngại kiến thức cần giải quyết)

• Ta thừa nhận tính chất: "0 < a ≠ 1 thì với mỗi số b > 0 ta luôn có duy nhất số α để a^α = b"
• Ví dụ 2^α = 16 thì α = 4

3^α = 27 thì α = 3

3^α = 12 thì α = ?

2^β = 20 thì β = ?

HĐ2: Là HĐ phát hiện khái niệm mới (giáo viên gợi ý dẫn dắt để học sinh phát hiện khái niệm mới.

• Từ đó GV gợi ý α được gọi là lôgarit cơ số 3 của 12

β được gọi là lôgarit cơ số 2 của 20

HĐ3: Là HĐ phát biểu định nghĩa khái niệm mới

• GV gọi học sinh phát biểu định nghĩa về lôgarit

HĐ 4: Củng cố và vận dụng khái niệm mới

• Chú ý: log_ab có nghĩa khi 0 < α ≠ 1 và b > 0
• GV cho một số ví dụ

log₃81 = α → α = 4 vì 3⁴ = 81

Bài 3: "Tìm m để phương trình có nghiệm thực"

Hướng dẫn học sinh theo các bước sau:

+ (1)

Số nghiệm PT (1) là số giao điểm của đồ thị (C): và (d): y = m

+ Xét

Tập xác định D = [1; 6]

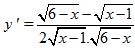
Lập bảng biến thiên hàm số.

+ Dựa vào bảng biến thiên kết luận giá trị m cần tìm là: √5 ≤ m ≤ √10

Bài 4:

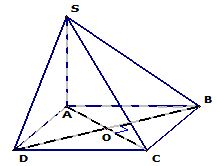
Cách 1:

• Kẻ AH ⊥ SD. Chứng minh AH ⊥ (SCD)
• Vậy d(A, (SCD)) = AH
• Xét tam giác SAD vuông tại A ta tính được

Cách 2:

• Tính thể tích khối chóp S.ACD:
• 
• Tính
• Suy ra d(A; (SCD)) =

Cách 3:

• Chọn không gian Axyz như hình vẽ
• Ta có A(0; 0; 0); S(0; 0; √2); D(A; 0; 0); C(a; a; 0)
• Tìm PT mp(SCD): √2x + z - a√2 = 0
• d(A; (SCD)) =