Giải bài tập tài liệu dạy học Toán lớp 7 bài tập - Chủ đề 11: Đa thức
Giải bài tập tài liệu dạy học Toán 7 bài tập - Chủ đề 11: Đa thức
Giải bài tập tài liệu dạy học Toán lớp 7 bài tập - Chủ đề 11: Đa thức với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán lớp 7. Lời giải hay bài tập Toán 7 này gồm các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán. Mời các bạn tham khảo
Bài tập 1 trang 77 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Tìm bậc của mỗi đã thức sau:
Đề bài
Tìm bậc của mỗi đã thức sau:
\(\eqalign{ & a)\,\,M = 3{x^3} - 4xy + 12{x^2}y - 1 \cr & b)\,\,N = 7{x^2}{y^2} - 4{x^3}y + 9{y^4} + 7{x^2}y + 13 \cr}\)
Lời giải chi tiết
a) Đa thức \(M = 3{x^3} - 4xy + 12{x^2}y - 1\)
Trong đó, hạng tử 3x3 có bậc 3, hạng tử -4xy2 có bậc 3, hạng tử 12x2y có bậc là 3 và hạng tử -1 có bậc là 0.
Bậc cao nhất trong các bậc vừa nêu là 3. Ta nói đa thức M có bậc là 3.
\(b)\,\,N = 7{x^2}{y^2} - 4{x^3}y + 9{y^4} + 7{x^2}y + 13\)
Trong đó, hạng tử 7x2y2 có bậc là 4, hạng tử -4x3y có bậc là 4, hạng tử 9y4 có bậc là 4, hạng tử 7x2y có bậc là 3 và hạng tử 13 có bậc là 0.
Bậc cao nhất trong các bậc vừa nêu là 4. Ta nói đa thức N có bậc là 4.
Đề bài
Cho đa thức:
\(A = {2 \over 3}{x^2}{y^2} - {1 \over 3}x{y^2} + 2{x^2}{y^2} + 7{y^2}x - 14\)
a) Hãy thu gọn đa thức A.
b) Tìm bậc của A.
Lời giải chi tiết
Bài tập 2 trang 77 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho đa thức:
\(\eqalign{ & a)A = {2 \over 3}{x^2}{y^2} - {1 \over 3}x{y^2} + 3{x^2}{y^2} + 7{y^2}x - 14 = \left( {{2 \over 3}{x^2}{y^2} + 3{x^2}{y^2}} \right) + \left( { - {1 \over 3}x{y^2} + 7x{y^2}} \right) - 14 \cr & = \left( {{2 \over 3} + 3} \right){x^2}{y^2} + \left( { - {1 \over 3} + 7} \right)x{y^2} - 14 = {{11} \over 3}{x^2}{y^2} + {{20} \over 3}x{y^2} - 14 \cr}\)
b) Đa thức \(A = {2 \over 3}{x^2}{y^2} - {1 \over 3}x{y^2} + 3{x^2}{y^2} + 7{y^2}x - 14\) có dạng thu gọn là
\(A = {{11} \over 3}{x^2}{y^2} + {{20} \over 3}x{y^2} - 14\)
Trong đó, hạng tử \({{11} \over 3}{x^2}{y^2}\) có bậc là 4, hạng tử \({{20} \over 3}x{y^2}\)có bậc là 3 và hạng tử -14 có bậc 0.
Bậc cao nhất trong các bậc vừa nêu là 4. Ta nói đa thức A có bậc là 4.
Bài tập 3 trang 77 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho đa thức
Cho đa thức \(B = 5{x^2} - 4x + 2{x^2} - 3x + 1.\) Hãy thu gọn rồi tính giá trị của đa thức B tại x = -3
Lời giải chi tiết
\(B = 5{x^2} - 4x + 2{x^2} - 3x + 1 = (5{x^2} + 2{x^2}) + ( - 4x - 3x) + 1 = 7{x^2} - 7x + 1\)
Thay x = -3 vào đa thức B = 7x2 -7x + 1 ta có: B = 7.(-3)2 -7.(-3) + 1 = 85
Vậy giá trị của đa thức B tại x = -3 là 85.
Bài tập 4 trang 77 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho đa thức:
Đề bài
Cho đa thức:
\(P = - 7x{y^2} + 5xy + 3x{y^2} - xy + 8\)
Hãy thu gọn rồi tính giá trị của đa thức P tại x = 2 và y = -1.
Lời giải chi tiết
\(P = - 7x{y^2} + 5xy + 3x{y^2} - xy + 8 = ( - 7x{y^2} + 3x{y^2}) + (5xy - xy) + 8 = - 4x{y^2} + 4xy + 8\)
Thay x = 2 và y = -1 vào đa thức
P = -4xy2 +4xy + 8
Ta có: P = -4.2.(-1)2 +4.2.(-1) + 8 = -8
Vậy giá trị của đa thức P tại x = 2 và y = -1 là -8.
Bài tập 5 trang 77 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Một cánh cửa sổ bằng gỗ với kích thước là 2x và 3y. Bên trong cánh cửa, người ta gắn hai tấm kính. Tấm kính thứ nhất có kích thước là (x + 1) và (x + 1) và tấm kính thứ hai có kích thước là (x + 1) và (2y) (xem hình vẽ).
Đề bài
Một cánh cửa sổ bằng gỗ với kích thước là 2x và 3y. Bên trong cánh cửa, người ta gắn hai tấm kính. Tấm kính thứ nhất có kích thước là (x + 1) và (x + 1) và tấm kính thứ hai có kích thước là (x + 1) và (2y) (xem hình vẽ).
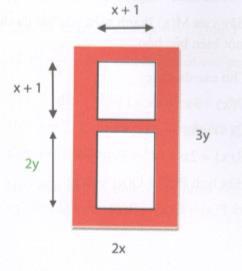
Hãy viết biểu thức đại số biểu thị diện tích phần gỗ của cánh cửa.
Biểu thức ấy có phải là một đa thức không?
Lời giải chi tiết
Tấm kính thứ nhất có kích thước là (x + 1) và (x + 1) nên có diện tích là
(x + 1).(x +1) = (x + 1)2
Tấm kính thứ hai có kích thước là (x + 1) và 2y nên có diện tích là 2y(x + 1)
Cánh cửa sổ có kích thước là 2x và 3y nên có diện tích là: 2x.3y = 6xy
Diện tích phần gỗ của cánh cửa là:
6xy – (x + 1)2 – 2y(x + 1)
Ta có:
\(\eqalign{ & 6xy{\rm{ }}-{\rm{ }}{\left( {x{\rm{ }} + {\rm{ }}1} \right)^2}-{\rm{ }}2y\left( {x{\rm{ }} + {\rm{ }}1} \right) = 6xy - ({x^2} + 2x + 1) - 2yx - 2y \cr & = 6xy - {x^2} - 2x - 1 - 2xy - 2y = 8xy - {x^2} - 2x - 2y - 1 \cr}\)
Biểu thức \(8xy - {x^2} - 2x - 2y - 1\) là một tổng của những đơn thức nên biểu thức \(8xy - {x^2} - 2x - 2y - 1\) là một đa thức.
* Chú ý: Từ 6xy – (x + 1)2 – 2y(x + 1) cũng kết luận được đây là đa thức
Bài tập 6 trang 77 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Biểu thức có được gọi là đa thức hay không?
Đề bài
Biểu thức \(2{x^2}y - 2x\sqrt y + xy - 10\)\(2{x^2}y - 2x\sqrt y + xy - 10\) có được gọi là đa thức hay không?
Lời giải chi tiết
Vì biểu thức \(2{x^2}y - 2x\sqrt y + xy - 10\)có một số hạng là \(- 2x\sqrt y\) không phải là đơn thức nên biểu thức \(2{x^2}y - 2x\sqrt y + xy - 10\) không được gọi là đa thức.
Bài tập 7 trang 77 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Biểu thức có được gọi là đa thức hay không?
Đề bài
Biểu thức \(5x{y^3} - 4y.{1 \over {x + 2}} - {x^2}y + 2\) có được gọi là đa thức hay không?
Lời giải chi tiết
Vì biểu thức \(5x{y^3} - 4y.{1 \over {x + 2}} - {x^2}y + 2\) có một số hạng là \(- 4y.{1 \over {x + 2}}\) không phải là đơn thức nên biểu thức \(5x{y^3} - 4y.{1 \over {x + 2}} - {x^2}y + 2\) không được gọi là đa thức.
Bài tập 8 trang 77 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Tính tổng của M và N.
Đề bài
Cho \(M = 5{x^2} - 8{x^2}y - 2y + 3\) và \(N = 3y + 5{x^2}y + 13\). Tính tổng của M và N.
Lời giải chi tiết
M + N = (5x2 – 8x2y – 2y + 3) + (3y + 5x2y+13)
= 5x2 – 8x2y – 2y + 3 + 3y + 5x2y + 13 (Bỏ dấu ngoặc)
= 5x2 +(– 8x2y + 5x2y) + (-2y + 3y) +(3+13) (Nhóm các cặp hạng tử đồng dạng)
= 5x2 – 3x2y + y + 16 (thực hiện phép cộng các đơn thức đồng dạng)
Ta nói đa thức 5x2 – 3x2y + y + 16 là tổng của hai đa thức M và N.
Bài tập 9 trang 77 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Tính A + B và A – B.
Đề bài
Cho \(A = - 2xyz + 4{x^2} - 8y + 3\) và \(B = 2xyz - 9y + 7x + 11\)
Tính A + B và A – B.
Lời giải chi tiết
A + B
= (-2xyz + 4x2 - 8y + 3)+(2xyz–9y+7x+11)
= -2xyz + 4x2 - 8y + 3 + 2xyz – 9y + 7x +11 (Bỏ dấu ngoặc)
= (-2xyz + 2xyz) + 4x2+(-8y-9y)+(3+11)+7x (Nhóm các cặp hạng tử đồng dạng)
= 4x2 – 17y + 14 + 7x.
A – B
= (-2xyz + 4x2 - 8y + 3)-(2xyz–9y+7x+11)
= -2xyz + 4x2 - 8y + 3 - 2xyz + 9y - 7x -11 (Bỏ dấu ngoặc)
= (-2xyz - 2xyz) + 4x2+(-8y+9y)+(3-11)-7x (Nhóm các cặp hạng tử đồng dạng)
= -4xyz + 4x2 + y -8 – 7x.
Bài tập 10 trang 77 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Tìm đa thức P, biết rằng:
Đề bài
Tìm đa thức P, biết rằng:
\({x^2} - {y^2} + 4xy + P = {1 \over 3}{x^2} - 6xy - 3{y^2} + 2x + 3\)
Lời giải chi tiết
\(\eqalign{ & {x^2} - {y^2} + 4xy + P = {1 \over 3}{x^2} - 6xy - 3{y^2} + 2x + 3 \cr & ({x^2} - {y^2} + 4xy) + P = ({1 \over 3}{x^2} - 6xy - 3{y^2} + 2x + 3) \cr & P = ({1 \over 3}{x^2} - 6xy - 3{y^2} + 2x + 3) - ({x^2} - {y^2} + 4xy) \cr & P = {1 \over 3}{x^2} - 6xy - 3{y^2} + 2x + 3 - {x^2} + {y^2} - 4xy \cr & P = ({1 \over 3}{x^2} - {x^2}) + ( - 6xy - 4xy) + ( - 3{y^2} + {y^2}) + 2x + 3 \cr & P = - {2 \over 3}{x^2} - 10xy - 2{y^2} + 2x + 3. \cr}\)
Bài tập 11 trang 77 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Tìm đa thức Q, biết rằng:
Đề bài
Tìm đa thức Q, biết rằng:
\(Q - (2{x^4} - 3{x^2}{y^2} + 5{x^2}y - 4x + 2) = 2{x^2}{y^2} + 5x - 7y - {x^2}y\)
Lời giải chi tiết
\(\eqalign{ & Q - (2{x^4} - 3{x^2}{y^2} + 5{x^2}y - 4x + 2) = 2{x^2}{y^2} + 5x - 7y - {x^2}y \cr & Q = 2{x^2}{y^2} + 5x - 7y - {x^2}y + (2{x^4} - 3{x^2}{y^2} + 5{x^2}y - 4x + 2) \cr & Q = 2{x^2}{y^2} + 5x - 7y - {x^2}y + 2{x^4} - 3{x^2}{y^2} + 5{x^2}y - 4x + 2 \cr & Q = (2{x^2}{y^2} - 3{x^2}{y^2}) + (5x - 4x) - 7y + ( - {x^2}y + 5{x^2}y) + 2{x^4} + 2 \cr & Q = - {x^2}{y^2} + x - 7y + 4{x^2}y + 2{x^4} + 2. \cr}\)
Bài tập 12 trang 77 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Tính tổng của hai đa thức sau:
Đề bài
Tính tổng của hai đa thức sau:
\(\eqalign{ & M = 2{x^2} - 3x{y^2} + 3{x^2}y - 3y + 2 \cr & N = 4{x^2}{y^2} - 2x{y^2} + 3{x^2}y - 4x + 2y \cr}\)
Lời giải chi tiết
\(\eqalign{ & M + N = (2{x^2} - 3x{y^2} + 3{x^2}y - 3y + 2) + (4{x^2}{y^2} - 2x{y^2} + 3{x^2}y - 4x + 2y) \cr & = 2{x^2} - 3x{y^2} + 3{x^2}y - 3y + 2 + 4{x^2}{y^2} - 2x{y^2} + 3{x^2}y - 4x + 2y \cr & = 2{x^2} + ( - 3x{y^2} - 2x{y^2}) + (3{x^2}y + 3{x^2}y) + ( - 3y + 2y) + 2 + 4{x^2}{y^2} - 4x \cr & = 2{x^2} - 5x{y^2} + 6{x^2}y - y + 2 + 4{x^2}{y^2} - 4x. \cr}\)
Ta nói đa thức \(2{x^2} - 5x{y^2} + 6{x^2}y - y + 2 + 4{x^2}{y^2} - 4x\) là tổng của hai đa thức M và N.
Bài tập 13 trang 77 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho đa thức:
Đề bài
Cho đa thức:
\(P = 3x{y^3} - 4{x^2}{y^2} + 2{x^2}y - 2xy + 9\)
Tính giá trị của P tại x = -2 và y = 3.
Lời giải chi tiết
Thay x = -2 và y = 3 vào đa thức \(P = 3x{y^3} - 4{x^2}{y^2} + 2{x^2}y - 2xy + 9\)
Ta có: \(P = 3.( - 2){.3^3} - 4.{( - 2)^2}{.3^2} + 2.{( - 2)^2}.3 - 2.( - 2).3 + 9 = - 261\)
Vậy giá trị của đa thức \(P = 3x{y^3} - 4{x^2}{y^2} + 2{x^2}y - 2xy + 9\) là -261
Bài tập 14 trang 77 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Viết một đa thức bậc bốn với hai biến số x, y và có năm hạng tử.
Đề bài
Viết một đa thức bậc bốn với hai biến số x, y và có năm hạng tử.
Lời giải chi tiết
Một đa thức bậc bốn với hai biến số x, y và có năm hạng tử là:
\(5{x^2}{y^2} - 3{x^2}y + {1 \over 2}{x^2} - xy + 7.\)
Bài tập 15 trang 77 Tài liệu dạy – học Toán 7 tập 2
a) Tìm đa thức R, biết rằng R – Q = P.
Đề bài
Cho \(P = 6{x^2}y - 4xy + 9{x^2} - 7y + 1\) và \(Q = - 3xy - 8{y^2}x - 5y + x - 11\)
a) Tìm đa thức R, biết rằng R – Q = P.
b) Tìm đa thức M, biết rằng P + M = Q.
Lời giải chi tiết
\(\eqalign{ & a)R - Q = P \cr & R = P + Q \cr & R = (6{x^2}y - 4xy + 9{x^2} - 7y + 1) + ( - 3xy - 8{y^2}x - 5y + x - 11) \cr & R = 6{x^2}y - 4xy + 9{x^2} - 7y + 1 - 3xy - 8{y^2}x - 5y + x - 11 \cr & R = 6{x^2}y + ( - 4xy - 3xy) + 9{x^2} + ( - 7y - 5y) + (1 - 11) - 8{y^2}x + x \cr & R = 6{x^2}y - 7xy + 9{x^2} - 12y - 10 - 8{y^2}x + x. \cr & b)P + M = Q \cr & M = Q - P \cr & M = ( - 3xy - 8{y^2}x - 5y + x - 11) - (6{x^2}y - 4xy + 9{x^2} - 7y + 1) \cr & M = - 3xy - 8{y^2}x - 5y + x - 11 - 6{x^2}y + 4xy - 9{x^2} + 7y - 1 \cr & M = ( - 3xy + 4xy) - 8{y^2}x + ( - 5y + 7y) + x + ( - 11 - 1) - 6{x^2}y - 9{x^2} \cr & M = xy - 8{y^2}x + 2y + x - 12 - 6{x^2}y - 9{x^2}. \cr}\)
Bài tập 16 trang 78 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Trong mảnh đất hình chữ nhật có độ dài các cạnh là x (c) và y (cm), người ta đào một cái giếng hình tròn có bán kính là r (cm). Tính diện tích S còn lại của mảnh đất theo x, y và r. Diện tích S có phải là một đa thức không?
Đề bài
Trong mảnh đất hình chữ nhật có độ dài các cạnh là x (c) và y (cm), người ta đào một cái giếng hình tròn có bán kính là r (cm). Tính diện tích S còn lại của mảnh đất theo x, y và r. Diện tích S có phải là một đa thức không?
Lời giải chi tiết
Giếng hình tròn có bán kính là r nên có diện tích là 3,14.r.r = 3,14r2 (cm2)
Mảnh đất hình chữ nhật có kích thước là x(cm) và y(cm) nên có diện tích là xy (cm2)
Diện tích còn lại của mảnh đất là:
S = xy – 3,14r2 (cm2)
Theo đó, diện tích S = xy – 3,14r2 là một đa thức vì biểu thức S = xy – 3,14r2 là tổng của những đơn thức.
Bài tập 17 trang 78 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho đa thức
Đề bài
Cho đa thức
\(P\left( x \right) = 5x - 7{x^4} + 8{x^3} - 2{x^2} - 4{x^3} + 6{x^4} - 9x + 6\)
a) Hãy thu gọn và sắp xếp các hạng tử của P(x) theo lũy thừa giảm dần của biến.
b) Nêu các hệ số của P(x)
Lời giải chi tiết
\(\eqalign{ & a)P\left( x \right) = 5x - 7{x^4} + 8{x^3} - 2{x^2} - 4{x^3} + 6{x^4} - 9x + 6 \cr & = (5x - 9x) + ( - 7{x^4} + 6{x^4}) + (8{x^3} - 4{x^3}) - 2{x^2} + 6 = - 4x - {x^4} + 4{x^3} - 2{x^2} + 6 \cr}\)
Đa thức \(P\left( x \right) = 5x - 7{x^4} + 8{x^3} - 2{x^2} - 4{x^3} + 6{x^4} - 9x + 6\) có dạng thu gọn là \(P(x) = - 4x - {x^4} + 4{x^3} - 2{x^2} + 6.\)
Khi sắp xếp theo lũy thừa giảm dần của biến ta có: \(P(x) = - {x^4} + 4{x^3} - 2{x^2} - 4x + 6\)
b) Các hệ số của P(x): -1 là hệ số của lũy thừa bậc 4; 4 là hệ số của lũy thừa bậc 3; -2 là hệ số của lũy thừa bậc 2; -4 là hệ số của lũy thừa bậc 1 và 6 là hệ số của lũy thừa bậc 0 (còn được gọi là hệ số tự do).
Bài tập 18 trang 78 Tài liệu dạy – học Toán 7 tập 2
Cho đa thức
Đề bài
Cho đa thức
\(Q\left( x \right) = - 5{x^5} + 4{x^3} - 8{x^2} - 12{x^3} - 9{x^2} + 7\)
a) Hãy thu gọn và sắp xếp các hạng tử của Q(x) theo lũy thừa tăng dần của biến.
b) Nêu các hệ số của Q(x).
Lời giải chi tiết
\(\eqalign{ & a)Q\left( x \right) = - 5{x^5} + 4{x^3} - 8{x^2} - 12{x^3} - 9{x^2} + 7 \cr & = - 5{x^5} + (4{x^3} - 12{x^3}) + ( - 8{x^2} - 9{x^2}) + 7 = - 5{x^5} - 8{x^3} - 17{x^2} + 7 \cr}\)
Thu gọn đa thức: \(Q\left( x \right) = - 5{x^5} + 4{x^3} - 8{x^2} - 12{x^3} - 9{x^2} + 7 = - 5{x^5} - 8{x^3} - 17{x^2} + 7\)
Sắp xếp theo lũy thừa tăng dần của biến ta có: \(Q(x) = 7 - 17{x^2} - 8{x^3} - 5{x^5}.\)
b) Các hệ số của Q(x) là: 7 là hệ số của bậc 0 (còn gọi là hệ số tự do); -17 là hệ số của bậc 2; -8 là hệ số của bậc 3 và 5 là hệ số của bậc 5.
Bài tập 19 trang 78 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Hãy viết một đa thức một biến có ba hạng tử với hệ số cao nhất là -8 và hệ số tự do là 5.
Đề bài
Hãy viết một đa thức một biến có ba hạng tử với hệ số cao nhất là -8 và hệ số tự do là 5.
Lời giải chi tiết
Một đa thức một biến có ba hạng tử với hệ số cao nhất là -8 và hệ số tự do là 5 viết được là:
-8x3 + 2x + 5.
Bài tập 20 trang 78 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho đa thức
Đề bài
Cho đa thức \(M\left( x \right) = {x^4} - 8{x^2} + 16.\) Tính giá trị của đa thức tại x = 2 và tại x=-1.
Lời giải chi tiết
Ta có M(2) = 24 - 8.22 + 16 = 0
Vậy giá trị của đa thức \(M\left( x \right) = {x^4} - 8{x^2} + 16\) tại x = 2 là 0.
Ta có M(-1) = (-1)4 - 8.(-1)2 + 16 = 9
Vậy giá trị của đa thức \(M\left( x \right) = {x^4} - 8{x^2} + 16\) tại x = -1 là 9.
Bài tập 21 trang 78 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho đa thức P(x) = 6x – 1 thì P(x) có bậc là:
Đề bài
Cho đa thức P(x) = 6x – 1 thì P(x) có bậc là:
a) 6 b) 1 c) -1
Lời giải chi tiết
Đa thức P(x) = 6x – 1.
Trong đó, hạng tử 6x có bậc là 1 và hạng tử -1 có bậc là 0.
Bậc cao nhất trong hai bậc vừa nêu là 1.
Ta nói đa thức P(x) có bậc là 1. Chọn đáp án b).
Bài tập 22 trang 78 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho đa thức
Đề bài
Cho đa thức \(Q\left( x \right) = 5x - 4 + 3{x^2}\) thì Q(x) có bậc là:
a) 5 b) 3 c) 2
Lời giải chi tiết
Đa thức Q(x) = 5x – 4 + 3x2. Trong đó, hạng tử 5x có bậc là 1, hạng tử -4 có bậc là 0 và hạng tử 3x2 có bậc là 2.
Bậc cao nhất trong hai bậc vừa nêu là 2.
Ta nói đa thức Q(x) có bậc là 2 => Chọn đáp án c).
Bài tập 23 trang 78 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho đa thức
Đề bài
Cho đa thức \(M\left( x \right) = 3{x^3} + 8{x^2} - 3x + 11\) thì M(x) có hệ số cao nhất là:
a) 11 b) 3 c) 8
Lời giải chi tiết
Đa thức M(x) = 3x3 + 8x2 – 3x +11 thu gọn. Trong đó, hạng tử 3x3 có bậc là 3, hạng tử 8x2 có bậc là 2, hạng tử -3x có bậc là 1 và hạng tử 11 có bậc là 0.
Bậc cao nhất trong hai bậc vừa nêu là 3.
Ta nói đa thức M(x) có bậc là 3 => Chọn đáp án b).
Bài tập 24 trang 78 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho hai đa thức
Đề bài
Cho hai đa thức \(M\left( x \right) = {x^2} + 7{x^4} - 2x - 10\) và \(N\left( x \right) = 3x + 4{x^4} - 2{x^3} + 7\)
Hãy tính M(x) + N(x) và M(x) - N(x)
Lời giải chi tiết
M(x) + N(x) = (x2 + 7x4 − 2x − 10) + (3x + 4x4 − 2x3 + 7) = x2 + 7x4 −2x −10 + 3x + 4x4 −2x3 + 7 = x2 + (7x4 + 4x4) + (−2x + 3x) + (−10 + 7) − 2x3 = x2 + 11x z4 + x − 3 − 2x3 . M(x) − N(x) = (x2 + 7x4 − 2x − 10) − (3x + 4x4 − 2x3 + 7) = x2 + 7x4 − 2x − 10 − 3x − 4x4 + 2x3 − 7 = x2 + (7x4 − 4x4) + (−2x −3x) + (−10 −7) + 2x3 = x2 + 3x4 − 5x − 17 + 2x3.
Bài tập 25 trang 78 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho đa thức
Đề bài
Cho đa thức \(P\left( x \right) = - 4{x^2} + 5{x^3} - 3x - 2\)
Tìm đa thức Q(x) sao cho
\(Q\left( x \right) - P\left( x \right) = 2x + {x^2} - 3{x^4} - 4\)
Lời giải chi tiết
\(\eqalign{ & Q\left( x \right) - P\left( x \right) = 2x + {x^2} - 3{x^4} - 4 \cr & Q(x) = 2x + {x^2} - 3{x^4} - 4 + P(x) \cr & Q(x) = 2x + {x^2} - 3{x^4} - 4 + ( - 4{x^2} + 5{x^3} - 3x - 2) \cr & Q(x) = 2x + {x^2} - 3{x^4} - 4 - 4{x^2} + 5{x^3} - 3x - 2 \cr & Q(x) = (2x - 3x) + ({x^2} - 4{x^2}) - 3{x^4} + ( - 4 - 2) + 5{x^3} \cr & Q(x) = - x - 3{x^2} - 3{x^4} - 6 + 5{x^3}. \cr}\)
Bài tập 26 trang 78 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho đa thức
Đề bài
Cho đa thức
\(M\left( x \right) = - 2{x^4} + 4{x^2} - 5x + {3 \over {10}}\)
Tìm đa thức N(x) sao cho
\(M\left( x \right) + N\left( x \right) = 7 - 12x + {x^2} - {x^4}\)
Lời giải chi tiết
\(\eqalign{ & M\left( x \right) + N\left( x \right) = 7 - 12x + {x^2} - {x^4} \cr & N(x) = 7 - 12x + {x^2} - {x^4} - M(x) \cr & N(x) = 7 - 12x + {x^2} - {x^4} - ( - 2{x^4} + 4{x^2} - 5x + {3 \over {10}}) \cr & N(x) = 7 - 12x + {x^2} - {x^4} + 2{x^4} - 4{x^2} + 5x - {3 \over {10}} \cr & N(x) = \left( {7 - {3 \over {10}}} \right) + ( - 12x + 5x) + ({x^2} - 4{x^2}) + ( - {x^4} + 2{x^4}) \cr & N(x) = {{67} \over {10}} - 7x - 3{x^2} + {x^4}. \cr}\)
Bài tập 27 trang 78 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho đa thức
Đề bài
Cho đa thức \(P\left( x \right) = 4x + {2 \over 5}{x^2} - 3{x^3} + 1\)
Hãy viết P(x) thành tổng của hai đa thức một biến bậc bốn.
Lời giải chi tiết
\(P\left( x \right) = 4x + {2 \over 5}{x^2} - 3{x^3} + 1 = (4x + {2 \over 5}{x^2} - {x^4}) + ({x^4} - 3{x^3} + 1).\)
Bài tập 28 trang 78 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho đa thức
Đề bài
Cho đa thức \(M\left( x \right) = 6 + 4x - 9{x^2} + 5{x^3}\)
Hãy viết M(x) thành hiệu của hai đa thức một biến bậc bốn.
Lời giải chi tiết
\(M\left( x \right) = 6 + 4x - 9{x^2} + 5{x^3} = (6 + 4x + {x^4}) - ({x^4} + 9{x^2} - 5{x^3}).\)
Bài tập 29 trang 78 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho các đa thức
Đề bài
Cho các đa thức
\(\eqalign{ & P\left( x \right) = 3{x^2} - 4x + 1 \cr & Q\left( x \right) = 5{x^3} - 2x - 4 \cr & R\left( x \right) = 2x - 7{x^4} + 3 \cr}\)
Hãy tính P(x) + Q(x) + R(x) và
P(x) - Q(x) - R(x).
Lời giải chi tiết
\(\eqalign{ & P(x) + Q(x) + R(x) = (3{x^2} - 4x + 1) + (5{x^3} - 2x - 4) + (2x - 7{x^4} + 3) \cr & = 3{x^2} - 4x + 1 + 5{x^3} - 2x - 4 + 2x - 7{x^4} + 3 \cr & = 3{x^2} + ( - 4x - 2x + 2x) + (1 - 4 + 3) + 5{x^3} - 7{x^4} = 3{x^2} - 4x + 5{x^3} - 7{x^4}. \cr & P(x) - Q(x) - R(x) = (3{x^2} - 4x + 1) - (5{x^3} - 2x - 4) - (2x - 7{x^4} + 3) \cr & = 3{x^2} - 4x + 1 - 5{x^3} + 2x + 4 - 2x + 7{x^4} - 3 \cr & = 3{x^2} + ( - 4x + 2x - 2x) + (1 + 4 - 3) - 5{x^3} + 7{x^4} = 3{x^2} - 4x + 2 - 5{x^3} + 7{x^4}. \cr}\)
Bài tập 30 trang 79 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho các đa thức
Đề bài
Cho các đa thức
\(M\left( x \right) = 4x - 9{x^4} + 2{x^2};\)
\(N\left( x \right) = 5 + 2{x^2} - 8x + {x^4}\)
a) Hãy sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
b) Hãy tính M(x) + N(x) và M(x) – N(x).
Lời giải chi tiết
a) Đa thức \(M\left( x \right) = 4x - 9{x^4} + 2{x^2}\) khi xếp theo lũy thừa tăng của biến M \(\left( x \right) = 4x + 2{x^2} - 9{x^4}\).
Đa thức \(N\left( x \right) = 5 + 2{x^2} - 8x + {x^4}\) khi xếp theo lũy thừa tăng của biến \(N\left( x \right) = 5 - 8x + 2{x^2} + {x^4}.\)
b) Cách 1:
\(\eqalign{ & M(x) + N(x) = (4x - 9{x^4} + 2{x^2}) + (5 + 2{x^2} - 8x + {x^4}) \cr & = 4x - 9{x^4} + 2{x^2} + 5 + 2{x^2} - 8x + {x^4} \cr & = (4x - 8x) + ( - 9{x^4} + {x^4}) + (2{x^2} + 2{x^2}) + 5 = - 4x - 8{x^4} + 4{x^2} + 5 = 5 - 4x + 4{x^2} - 8{x^4} \cr}\)
• Cách 2:
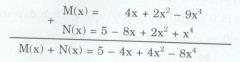
• Cách 1:
\(\eqalign{ & M(x) - N(x) = (4x - 9{x^4} + 2{x^2}) - (5 + 2{x^2} - 8x + {x^4}) \cr & = 4x - 9{x^4} + 2{x^2} - 5 - 2{x^2} + 8x - {x^4} \cr & = (4x + 8x) + ( - 9{x^4} - {x^4}) + (2{x^2} - 2{x^2}) - 5 = 12x - 10{x^4} - 5 = - 5 + 12x - 10{x^4} \cr}\)
• Cách 2:
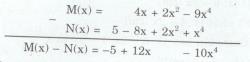
Bài tập 31 trang 79 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho các đa thức
Đề bài
Cho các đa thức
\(P\left( x \right) = 3 - 2{x^4} - 5{x^3} + 8{x^2};\)
\(Q\left( x \right) = 3{x^2} - 4x + 7{x^4} + 1.\)
Hãy tính \(Q(x) – P(x); P(x) – Q(x)\) và đưa ra nhận xét về các hệ số của hai đa thức vừa tìm.
Lời giải chi tiết
\(\eqalign{ & Q(x) - P(x) = (3{x^2} - 4x + 7{x^4} + 1) - (3 - 2{x^4} - 5{x^3} + 8{x^2}) \cr & = 3{x^2} - 4x + 7{x^4} + 1 - 3 + 2{x^4} + 5{x^3} - 8{x^2} \cr & = (3{x^2} - 8{x^2}) - 4x + (7{x^4} + 2{x^4}) + (1 - 3) + 5{x^3} \cr & = - 5{x^2} - 4x + 9{x^4} - 2 + 5{x^3} \cr & P(x) - Q(x) = (3 - 2{x^4} - 5{x^3} + 8{x^2}) - (3{x^2} - 4x + 7{x^4} + 1) \cr & = 3 - 2{x^4} - 5{x^3} + 8{x^2} - 3{x^2} + 4x - 7{x^4} - 1 \cr & = (3 - 1) + ( - 2{x^4} - 7{x^4}) - 5{x^3} + (8{x^2} - 3{x^2}) + 4x \cr & = 2 - 9{x^4} - 5{x^3} + 5{x^2} + 4x = 5{x^2} + 4x - 9{x^4} + 2 - 5{x^3} \cr}\)
* Nhận xét: Các hệ số của hai đa thức vừa tìm được đối nhau.
Bài tập 32 trang 79 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho hai đường tròn đồng tâm có bán kính lần lượt là x (cm) và 2x + 1 (cm). Tính diện tích hình vành khăn tạo bởi hai đường tròn nói trên.
Đề bài
Cho hai đường tròn đồng tâm có bán kính lần lượt là x (cm) và 2x + 1 (cm). Tính diện tích hình vành khăn tạo bởi hai đường tròn nói trên.
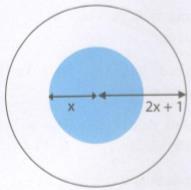
Lời giải chi tiết
Diện tích đương tròn lớn là:
3,14.(2x + 1).(2x + 1) = 3,14(2x + 1)2 (cm2).
Diện tích đường tròn nhỏ là:
3,14.x.x = 3,14x2 (cm2).
Diện tích đường vành khăn tạo bởi hai đường tròn nói trên là:
3,14(2x + 1)2 – 3,14x2
Bài tập 33 trang 79 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho đa thức
Đề bài
Cho đa thức\(P(x) = 2x + {1 \over 3}\). Tính \(P\left( {{1 \over 6}} \right)\)và\(P\left( {{{ - 1} \over 6}} \right)\). Hãy nêu nhận xét của em.
Lời giải chi tiết
\(\eqalign{ & P(x) = 2x + {1 \over 3} \cr & P\left( {{1 \over 6}} \right) = 2.{1 \over 6} + {1 \over 3} = {2 \over 3} \cr & P\left( {{{ - 1} \over 6}} \right) = 2.\left( {{{ - 1} \over 6}} \right) + {1 \over 3} = 0 \cr}\)
* Nhận xét: Đa thức \(P(x) = 2x + {1 \over 3}\) có nghiệm \(x = - {1 \over 6}\) vì \(P\left( {{{ - 1} \over 6}} \right) = 0\) và \(x = {1 \over 6}\) không phải lag nghiệm vì \(P\left( {{1 \over 6}} \right) = {2 \over 3} \ne 0\)
Bài tập 34 trang 79 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho đa thức
Đề bài
Cho đa thức \(P\left( x \right) = {x^2} - 5x + 6\). Hỏi x=2, x = 3 có phải là nghiệm của đa thức P(x) không?
Lời giải chi tiết
Đa thức \(P\left( x \right) = {x^2} - 5x + 6\)có x = 2 là nghiệm vì P(2) = 22 -5.2 + 6 = 0 và x = 3 là nghiệm vì P(3) = 32 – 5.3 + 6 = 0.
Bài tập 35 trang 79 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Hãy nêu đa thức khác nhau cùng có nghiệm là x = -2.
Đề bài
Hãy nêu đa thức khác nhau cùng có nghiệm là x = -2.
Lời giải chi tiết
Hai đa thức khác nhau cùng có nghiệm là x = -2 có thể là x + 2 và x2 + 4x + 4.
Bài tập 36 trang 79 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Hãy chứng tỏ đa thức
Đề bài
Hãy chứng tỏ đa thức \(P\left( x \right) = 2{x^4} + {x^2} + 1\) không có nghiệm.
Lời giải chi tiết
Đa thức P(x) = 2x4 + x2 + 1 không có nghiệm vì ta luôn có 2x4 ≥ 0, x2 ≥ 0.
Do đó P(x) = 2x4 + x2 + 1 > 0, với mọi giá trị của x.
Bài tập 37 trang 79 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Đa thức có nghiệm là:
Đề bài
Đa thức \(Q\left( x \right) = {x^4} + 4{x^2}\) có nghiệm là:
a) x = 2; b) x = -2; c) x = 0.
Lời giải chi tiết
Đa thức Q(x) = x4 + 4x2 có nghiệm là 0 vì Q(0) = 04 + 4.02 = 0 => Chọn đáp án c).
Cách khác: x4 + 4x2 = x2(x2 + 4) = 0
=> x2 = 0 => x = 0.
Bài tập 38 trang 79 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Tìm nghiệm của đa thức P(x) = 2x + 4.
Đề bài
Tìm nghiệm của đa thức P(x) = 2x + 4.
Lời giải chi tiết
P(x) = 0
2x + 4 = 0
2x = -4
x = -2
Nghiệm của đa thức P(x) là -2
Bài tập 39 trang 79 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Tìm nghiệm của đa thức
Đề bài
Tìm nghiệm của đa thức Q(y) = y2 − 9.
Lời giải chi tiết
Q(y) = 0
=> y2 – 9 = 0
=> y2 = 32
=> y = 3 hoặc y = -3
Nghiệm của đa thức Q(y) là 3 và -3.
Bài tập 40 trang 79 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Từ một tấm bìa hình chữ nhật có độ dài các cạnh là 4cm và 6cm, người ta cắt bỏ bốn hình vuông có độ dài cạnh là x (cm) nằm ở bốn góc của tấm bìa (xem hình vẽ) rồi xếp thành một hình hộp chữ nhật không có nắp.
Đề bài
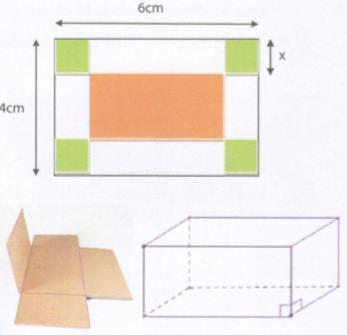
Từ một tấm bìa hình chữ nhật có độ dài các cạnh là 4cm và 6cm, người ta cắt bỏ bốn hình vuông có độ dài cạnh là x (cm) nằm ở bốn góc của tấm bìa (xem hình vẽ) rồi xếp thành một hình hộp chữ nhật không có nắp.
a) Tính thể tích V của hình hộp chữ nhật nói trên theo biến x.
b) Tính giá trị của V tại x = 1.
c) Hãy tính giá trị của x thỏa mãn:
V(x) – 8 = 0.
Lời giải chi tiết
a) Chiều dài hình hộp chữ nhật là: 6 – 2x (cm)
Chiều rộng của đáy hình hộp chữ nhật là: 4–2x (cm)
Hình hộp chữ nhật có các kích thước lần lượt là: 6 – 2x; 4- 2x và x
Nên có thể tích là:
V = (6- 2x).(4 – 2x).x (cm3).
b) Thay x = 1 vào biểu thức
V = (6- 2x).(4 – 2x).x ta có
V = (6- 2.1).(4 – 2.1).1 = 8
Vậy giá trị của V tại x = 1 là 8cm3
c) Theo câu b) có V(1) = 8. Do đó
V(1) – 8 = 0
Vậy một giá trị của x thỏa V(x) – 8 = 0 là x = 1.
............................
Mời các bạn tham khảo thêm tài liệu Toán 7:
Ngoài Giải bài tập tài liệu dạy học Toán lớp 7 bài tập - Chủ đề 11: Đa thức, các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 7 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu lớp 7 này giúp các bạn học tập và rèn luyện tốt kĩ năng học bài và làm bài. Chúc các bạn ôn tập tốt
